人教版 (五四制)八年级上册第二十二章 分式22.2 分式的运算精品ppt课件

22.2 分式的运算

22.2.3 整数指数幂 第2课时

一、教学目标

（一）学习目标

1. 利用10的乘方，进行科学记数，会用科学记数法表示小于1的数．

2．体会科学记数法的好处，化繁为简的方法．

（二）学习重点

会用科学记数法表示绝对值小于1的数．

（三）学习难点

正确使用科学记数法表示数．

二、教学设计

（一）课前设计

1.预习任务

（1）把一个绝对值大于10的数表示成形式（其中，n为正整数），叫科学记数法.

（2）仿照填空：

示范：

；

.

2.预习自测

（1）用科学记数法表示下列各数：0.0049；-0.0000093；0.00061.

【知识点】科学记数法.

【数学思想】化繁为简.

【解题过程】

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】

（2）据考证，单个雪花的质量为0.00036克左右，这个数用科学记数法表示为_____.

【知识点】科学记数法.

【数学思想】化繁为简.

【解题过程】

.

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】

（3）按要求取近似值，并将结果用科学计数法表示.

.

【知识点】科学记数法；取近似值.

【解题过程】

【思路点拨】

第一题先按要求取近似值即，再用科学记数法表示为第二题先用科学记数法表示为，再按要求取近似值为，第二题也可以先取近似值，再用科学记数法表示.

【答案】

（4）计算：（用科学记数法表示结果）

【知识点】科学记数法和幂的运算.

【解题过程】

【思路点拨】（1）利用乘法结合律3与6.2相乘得18.6，相乘得，最后把积相乘得；（2）先4÷5=0.8. 再把.

【答案】

(二)课堂设计

1.知识回顾.

用科学记数法表示下列各数.

（1）32 000=；   

（2）384000000=；

（3）－810 000=； 

2.问题探究

探究一

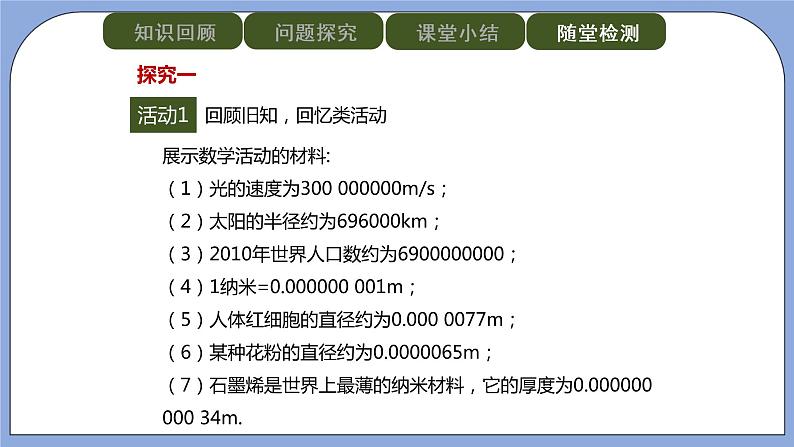
●活动① （回顾旧知，回忆类活动）

展示数学活动的材料（收集现实生活中较大或非常小的数据的实例）

（1）光的速度为300 000000m/s；（2）太阳的半径约为696000km；（3）2010年世界人口数约为6900000000；（4）1纳米=0.000000 001m；（5）人体红细胞的直径约为0.000 0077m；（6）某种花粉的直径约为0.0000065m；（7）石墨烯是世界上最薄的纳米材料，它的厚度为0.000000 000 34m.

让学生读出这些数，我们体会到这些数读起来比较困难，较大的数我们可以用科学记数法来表示，非常小的数也能用科学记数法表示吗？

【设计意图】通过展示生活中较大的数和非常小的数，激发学生的好奇心，再通过对这些数的读法，使学生感到读这些数时很不方便，创设良好的学习环境．

●活动② （整合旧知，探究类活动）

把下列各数变形成小数形式：

______；______；______；____；

由学生独立完成，然后展示学生答案：

【设计意图】为绝对值小于1的数用科学记数法作铺垫.

探究二

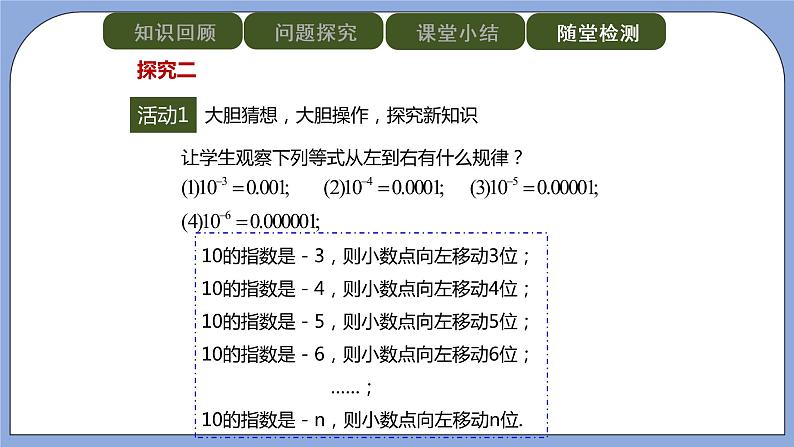
●活动① （大胆猜想，大胆操作，探究新知识）

让学生观察下列等式从左到右有什么规律？

让学生分组进行讨论，然后每组选一个代表交流，最后师生归纳：10的指数是-3，则小数点向左移动3位；10的指数是- 4，则小数点向左移动4位；10的指数是- 5，则小数点向左移动5位；10的指数是- 6，则小数点向左移动6位；……；10的指数是-n，则小数点向左移动n位.

【设计意图】从一些特殊数据出发，寻找解决问题的方法，有利于学生研究性学习能力的提高．

●活动② （集思广益，证明新知识）

教师指出：小于1的正数可以用科学记数法表示为：的形式，其中a是整数数位只有一位的数，n是正整数．利用科学记数法表示数，不仅简便，而且更便于比较数的大小，如：显然大于，前者是后者的10倍．

【设计意图】通过观察，发现利用10的负整数次幂表示小数的方法．这样不仅可以使书写简短，而且还便于读数．

●活动③ （反思过程，发现特征）

用科学记数法表示下列各数．

0.000000001；0.0012；0.000000345；-0.00003；0.0000000108.

学生独立完成，把解答过程写在课堂作业本上，教师巡视，对个别学生进行指导，最后展示解答过程：

解：0.000000001=10-9；0.0012=1.2×10-3；0.000000345=3.45×10-7；-0.00003=-3×10-5；0.0000000108=1.08×10-8．

【设计意图】通过练习，让学生对科学记数法有一定的认识．

●活动④ （发散思维，重新认识）

观察下列等式从左到右有什么发现？

0.000000001=10-9；

0.0012=1.2×10-3；

0.000000345=3.45×10-7；

﹣0.00003=﹣3×10-5；

0.0000000108=1.08×10-8．

让学生分组进行讨论，老师巡视，然后每组由一个代表发言交流，最后师生归纳：0.000 000 001到1小数点向右移动9位，则10的指数为﹣9；0.0012到1.2小数点向右移动3位，10的指数为-3；0.000 000345到3.45小数点向右移动7位，10的指数为﹣7；……；小数点向右移动n位，10的指数为-n.

【设计意图】通过观察与思考，让学生发现规律, 小数点向右移动n位，10的指数为-n.

探究三

●活动① （基础性例题）

我们学习小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．

利用本课定理可以解决一些怎样的问题?

例1 用科学记数法表示下列各数：

0．00004，   -0.034,     0.00000045,    0. 003009

【知识点】科学记数法

【解题过程】解：

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】

练习：用科学记数法表示下列各数：

0．0002 ，   -0.014,     0.0000065,    0.0049

【知识点】科学记数法.

【解题过程】解：

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】

【设计意图】会用科学记数法表示小于1的数.

●活动2 （提升型例题）

例2计算(结果用科学记数法表示)：

(1)(3×10-5)×(5×10-3)；

(2)(－1.8×10－10)÷(9×10－5)；

【知识点】科学记数法；乘法交换律；幂的运算.

【解题过程】

解：(1)原式＝15×10－8＝1.5×10－7；

(2)原式＝－0.2×10－5＝－2×10－6；

【思路点拨】(1)运用乘法交换律，3与5相乘，10－5与10－3相乘，再把积相乘，(2)-1.8与9相除，10－10相除10－5再把商相乘.

【答案】（1）1.5×10－7，（2）－2×10－6.

练习：计算(结果用科学记数法表示)：(2×10－3)－2×(－1.6×10－6)．

【知识点】科学记数法；乘法交换律；幂的运算.

【解题过程】

解:原式＝(×106)×(－1.6×10－6)＝－0.4＝－4×10－1.

【思路点拨】把第一个计算出来即(2×10－3)－2=×106 ， 再把与－1.6相乘，106与10－6相乘，最后把积相乘.

【答案】－4×10－1.

【设计意图】科学记数法和幂的综合运算.

●活动3 （探究型例题）

例3用四舍五入法按括号里的要求对下列各数取近似值.

（1）9850136（精确到万位）=______________;

（2）0.4371（精确到百分位）=_______________;

（3）-0.347218（精确到千分位）=________________.

【知识点】科学记数法；近似值.

【解题过程】

【思路点拨】精确到十位、百位、千位等，先用科学记数法表示，再取近似值；精确到十分位、百分位、千分位等，先取近似值，再用科学记数法.

【答案】

练习：用四舍五入法按括号里的要求对下列各数取近似值.

（1）1250176（精确到千位）=______________;

（2）0.4576（精确到百分位）=_______________;

（3）-0.036748（精确到千分位）=________________.

【知识点】科学记数法；近似值.

【思路点拨】精确到十位、百位、千位等，先用科学记数法表示，再取近似值；精确到十分位、百分位、千分位等，先取近似值，再用科学记数法.

【解题过程】解：

【答案】

【设计意图】进一步掌握科学记数法的表示方法.

例4. 国家质检总局出台了国内销售的纤维制品甲醛含量标准, 从2003年1月1 日起正式实施.该标准规定:针织内衣. 床上用品等直接接触皮肤的制品,甲醛含量应在百万分之七十五以下. 百万分之七十五用科学记数法表示应写成(    )
A、75×10－7；     B、75×10－6；     C、7.5×10－6；     D、7.5×10－5

【知识点】科学记数法.

【解题过程】

【思路点拨】首先要能正确表示百万分之七十五，它等于，再用科学记数法表示，小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】D

练习：自从扫描隧道显微镜发明后，世界上便诞生了一门新学科，这就是“纳米技术”.已知52个纳米长为0.000 000 052 m，用科学记数法表示此数为多少米？

【知识点】科学记数法

【数学思想】化繁为简的数学思想.

【解题过程】

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】米

【设计意图】利用科学记数法解决实际问题.

3. 课堂总结

知识梳理

（1）利用10的乘方，进行科学记数，会用科学记数法表示绝对值小于1的数．

（2）体会科学记数法的好处，化繁为简的方法．

重难点归纳

科学记数法不仅可以表示一个值大于10的数，也可以表示一些绝对值较小的数，在应用中，要注意a必须满足1≤|a|＜10，其中n是正整数．

（三）课后作业

基础型 自主突破

1．用科学记数法表示下列各数：

(1)0.0003267；(2)－0.0011；(3)－890600.

【知识点】科学记数法

【数学思想】化繁为简的数学思想.

【解题过程】

解：(1)0.0003267＝3.267×10－4；

(2)－0.0011＝－1.1×10－3；

(3)－890690＝－8.9069×105.

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】(1)0.0003267＝3.267×10－4；

(2)－0.0011＝－1.1×10－3；

(3)－890690＝－8.9069×105.

2．一枚一角硬币的直径约为0.022 m，用科学记数法表示为(   )

A．2.2×10－3 m       B．2.2×10－2 m     C．22×10－3 m      D．2.2×10－1 m

【知识点】科学记数法.

【数学思想】化繁为简的数学思想.

【解题过程】.

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】B

 3.科学记数法表示下列各数：

   0.000 000 18＝            ；56400 000 000＝            .

【知识点】科学记数法.

【数学思想】化繁为简的数学思想.

【解题过程】

【思路点拨】用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右(左)移动n位，10的指数就为-n（n）.

【答案】；

4.显微镜下测得一个圆球体细胞的直径是cm，个这样的细胞排成的细胞链的长是(    )

A．10－2 cm          B．10－1 cm       C．10－3 cm      D．10－4 cm

【知识点】科学记数法；幂的运算.

【解题过程】

【思路点拨】5与2相乘，相乘，再把积相乘.

【答案】B

5.用小数表示2.65×10－5=___________.

【知识点】负整数指数幂的性质.

【解题过程】解：

【思路点拨】把2.65的小数点向左移动5位得到即.

【答案】

6.科学记数法表示0.000695并保留两个有效数字为_________.

【知识点】科学记数法；取近似数.

【解题过程】

【思路点拨】先用科学记数法表示，再进行取近似值.

【答案】

能力型 师生共研

1.纳米是非常小的长度单位，1纳米＝米，把1立方纳米的物体放到乒乓球上，如同将乒乓球放到地球上，1立方毫米的空间可以放_______个1立方纳米的物体，（物体间的间隙忽略不计）.

【知识点】科学记数法；幂的运算.

【解答过程】

1立方纳米=，1立方毫米=，

【思路点拨】单位要保持一致，统一单位为立方米.

【答案】

2.（1）把数0.00237四舍五入到万分位，并用科学记数法表示为_________；

（2）把数0.03689保留两个有效数字，并用科学记数法表示为_________；

【知识点】科学记数法；取近似值.

【解答过程】

【思路点拨】

(1)先精确到万分位为0.0024，再用科学记数法表示为,(2)先用科学记数法表示为，再保留两个有效数字为.

【答案】

探究型 多维突破

1．计算：

；

【知识点】科学记数法和幂的运算.

【思路点拨】（1）利用乘法结合律3与5相乘，相乘，最后把积相乘；（2）先乘方后，再乘除.

【解题过程】

【答案】（1），（2）.

2．纳米是一种长度单位，1纳米＝10－9米．已知某花粉的直径为3500纳米，那么用科学记数法表示这种花粉的直径为__________米．

【知识点】科学记数法.

【解题过程】

∵1纳米＝10－9米，

∴3500纳米＝3500×10－9米．

而3500×10－9＝(3.5×103)×10－9＝3.5×103＋(－9)＝3.5×10－6，

∴这种花粉的直径为3.5×10－6米．

【思路点拨】因为1纳米＝10－9米，所以3500纳米表示为3500×10－9＝(3.5×103)×10－9

＝3.5×10－6.

【答案】3.5×10－6

自助餐

1．一枚扣子的直径约为0.023 m，用科学记数法表示为(   )

A．2.3×10－3 m　　       B．2.3×10－2 m

C．23×10－3 m           D．2.3×10－1 m

【知识点】科学记数法

【解题过程】

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】B

2．在电子显微镜下测得一个圆球体病毒细胞的直径是cm，个这样的病毒细胞排成的细胞链的长是(    )

A． cm              B．cm

C． cm              D．cm

【知识点】科学记数法

【解题过程】

【思路点拨】5与3相乘得15，相乘得，再把积相乘

【答案】B

3.用科学记数法表示下列各数：

（1）0.000 000 01＝           ；（2）0.012＝                   ；

（3）0.000 00365＝          ；（4）-0.0073＝                   .

【知识点】科学记数法.

【解题过程】

【思路点拨】小于1的正数用科学记数法表示的一般形式：a×10-n,a为整数数位只有一位的数,n为正整数．小数点向右移动n位，10的指数就为-n.

【答案】

4.用科学记数法表示0.000692并保留两个有效数字为________.

【知识点】科学记数法；取近似数.

【解题过程】

【思路点拨】先科学记数法表示为，再保留两个有效数字为.

【答案】.

5.纳米是一种长度单位，1纳米＝10－9米，一个粒子的直径是35纳米，它等于多少米？请用科学记数法表示．

【知识点】科学记数法

【解题过程】

解：∵1纳米＝10－9米，

∴35纳米＝35×10－9米,

而35×10－9＝(3.5×10)×10－9＝35×101＋(－9)＝3.5×10－8，

∴这个粒子的直径为3.5×10－8米．

【思路点拨】1纳米＝10－9米，35纳米表示为35×10－9米=米.

【答案】这个粒子的直径为3.5×10－8米

6.如果一根为1米长，直径为80毫米的光纤预制棒，可以拉成600千米长的光纤，试问：1平方厘米是这种光纤的横截面积的多少倍？（精确到万位）

【知识点】科学记数法；幂的运算.

【思路点拨】1米长，直径为80毫米的光纤预制棒的体积与600千米长的光纤的体积相等.

【数学思想】方程思想.

【解题过程】

解：设600千米长的光纤的横截面积为x平方米.

80毫米=，1平方厘米=

答：1平方厘米是这种光纤的横截面积的倍.

【答案】倍