人教版（五四学制）九上数学 31.1.4 圆周角第2课时 课件+教案

这是一份人教版（五四学制）九上数学 31.1.4 圆周角第2课时 课件+教案，文件包含人教版五四学制九上数学3114圆周角第2课时课件ppt、人教版五四学制九上数学3114圆周角第2课时教案doc等2份课件配套教学资源，其中PPT共26页， 欢迎下载使用。
31.1.4 圆周角
第二课时
（1）把顶点在圆上，并且两边都与圆相交的角叫做__________。（2）在同圆或等圆中，同弧所对的圆周角________，都等于这条弧所对的圆心角的________。（3）半圆（或直径）所对的圆周角是________，90°的圆周角所对的弦是_________。
圆周角
相等
一半
直角
直径
活动1
探究一:同圆或等圆中相等的圆周角所对的弧或弦、等弦所对的圆周角的关系
如图，⊙O1与⊙O2的半径相等，所以它们是等圆，∠A=∠D，证明：BC=EF，弧BC和弧EF相等。
在同圆或等圆中，同弧所对的圆周角相等，那么，相等的圆周角所对的弧也相等吗？
重点、难点知识★▲
大胆猜想 小心证明
活动1
探究一:同圆或等圆中相等的圆周角所对的弧或弦、等弦所对的圆周角的关系
结论：在同圆或等圆中，相等的圆周角所对的弧和弦相等.
证明：∵∠A=∠D，∴∠O1=∠O2∵⊙O1与⊙O2的半径相等，∴O1B= O1C= O2E= O2F∴△O1BC≌△O2EF∴BC=EF∴弧BC和弧EF相等
重点、难点知识★▲
大胆猜想 小心证明
活动2
探究一:同圆或等圆中相等的圆周角所对的弧或弦、等弦所对的圆周角的关系
有∠A、∠E、∠D，其中∠A=∠E
如图，⊙O中弦BC所对的圆周角有哪些？它们有什么关系？
重点、难点知识★▲
探索在同圆或等圆中，同弦所对圆周角的关系
那它们和∠D有什么关系呢？先猜想，再证明。
活动2
探究一:同圆或等圆中相等的圆周角所对的弧或弦、等弦所对的圆周角的关系
重点、难点知识★▲
探索在同圆或等圆中，同弦所对圆周角的关系
结论：在同圆或等圆中，等弦所对圆周角相等或互补.
解：如图，∠A与∠D不相等，它们互补.证明：∠A= ∠BOC, ∠D= （360°-∠BOC）∴∠A+∠D= ∠BOC+ （360°-∠BOC） = ×360°=180°∴∠A与∠D互补
活动1
探究二: 圆的内接多边形
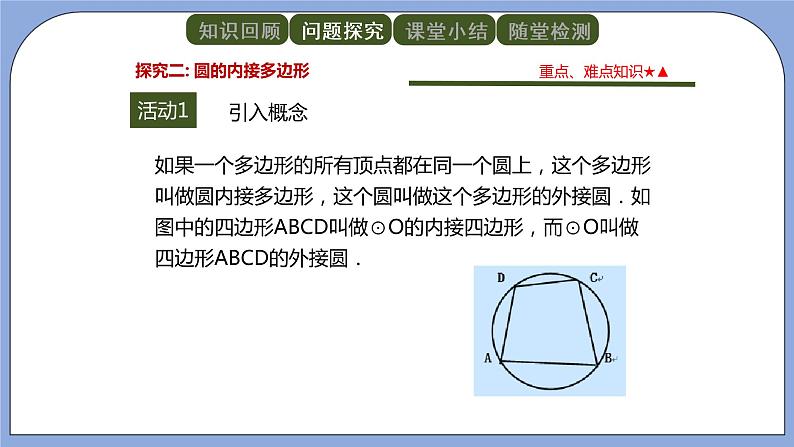
如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆．如图中的四边形ABCD叫做⊙O的内接四边形，而⊙O叫做四边形ABCD的外接圆．
重点、难点知识★▲
引入概念
活动2
探究二: 圆的内接多边形
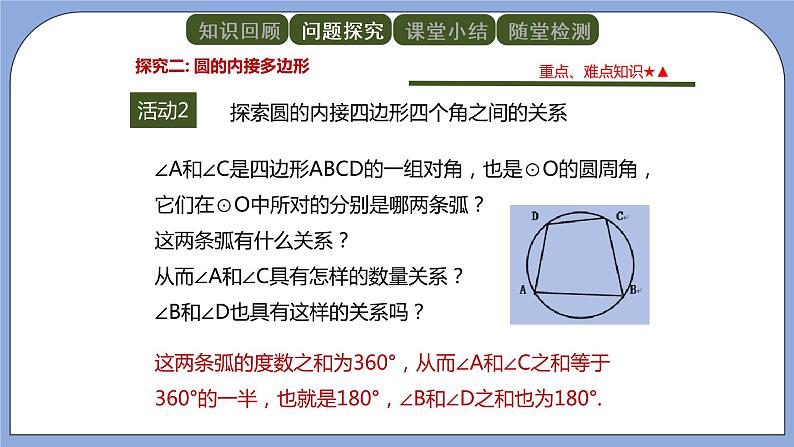
∠A和∠C是四边形ABCD的一组对角，也是⊙O的圆周角，它们在⊙O中所对的分别是哪两条弧？这两条弧有什么关系？从而∠A和∠C具有怎样的数量关系？∠B和∠D也具有这样的关系吗？
重点、难点知识★▲
探索圆的内接四边形四个角之间的关系
这两条弧的度数之和为360°，从而∠A和∠C之和等于360°的一半，也就是180°，∠B和∠D之和也为180°.
活动2
探究二: 圆的内接多边形
证明过程：
重点、难点知识★▲
探索圆的内接四边形四个角之间的关系
结论：圆的内接四边形对角互补.
活动1
探究三 例题分析
例1．同圆或等圆中，_______________所对的圆周角等于它所对的圆心角的一半．
基础性例题
同弧或等弧
【解题过程】解：同圆或等圆中，同弧或等弧所对的圆周 角等于它所对的圆心角的一半． 故答案为：同弧或等弧．
【思路点拨】利用圆周角定理判断即可得到结果．
活动1
探究三 例题分析
练习1：圆周角：（1）定理：一条弧所对的圆周角____________________________．（2）推论：①圆周角的度数等于它所对弧的度数的_________．②同弧或等弧所对的圆周角_________；在同圆或等圆中，相等的圆周角所对的__________．③直径所对的圆周角是_________；90°的圆周角所对的弦___________．④如果三角形一条边上的中线等于这条边的一半，那么______________________________．
基础性例题
等于它所对圆心角的一半
一半
相等
弧相等
90°
是直径
这个三角形是直角三角形
活动1
探究三 例题分析
例2．如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，在这8个角中，有几对相等的角？请把它们分别表示出来.
基础性例题
【解题过程】解：有4对．分别是：∠1=∠2，∠3=∠4， ∠5=∠6，∠7=∠8．
【思路点拨】观察图形，根据在同圆或等圆中，同弧或等弧所对的圆周角相等，即可求得答案．
活动1
探究三 例题分析
练习2．如图，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于E，若AB=2DE，∠E=18°，∠C=______，∠AOC=______．
基础性例题
【思路点拨】根据AB=2DE得DE等于圆的半径，在△EDO和△CEO中，根据三角形的一个外角等于和它不相邻的两个内角的和求解．
活动1
探究三 例题分析
【解题过程】解：连接OD，∵AB=2DE，∴OD=DE，∴∠E=∠EOD，在△EDO中，∠ODC=∠E+∠EOD=36°，∵OC=OD，∴∠OCD=∠ODC=36°，在△CEO中，∠AOC=∠E+∠OCD=18°+36°=54°．故答案为：36°；54°．
基础性例题
活动2
探究三 例题分析
例3.△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是（　　）A．80° B．160° C．100° D．80°或100°
提升型例题
【思路点拨】首先根据题意画出图形，由圆周角定理即可求得答案∠ABC的度数，又由圆的内接四边形的性质，即可求得∠ABC的度数．
活动2
探究三 例题分析
提升型例题
【解题过程】解：如图，∵∠AOC=160°，∴∠ABC= ∠AOC= ×160°=80°，∵∠ABC+∠AB′C=180°，∴∠AB′C=180°﹣∠ABC=180°﹣80°=100°．∴∠ABC的度数是：80°或100°．故选D．
活动2
探究三 例题分析
练习3：如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧 上一点，则∠APB的度数为（　　）A．45° B．30° C．75° D．60°
提升型例题
直角三角形三边的关系得到∠OAD=30°，接着根据三角形内角和定理可计算出∠AOB=120°，然后根据圆周角定理计算∠APB的度数．
【思路点拨】作半径OC⊥AB于D，连结OA、OB，如图，根据折叠的性质得OD=CD，则OD= OA，根据含30度的
【解题过程】解：作半径OC⊥AB于D，连结OA、OB，如图，∵将⊙O沿弦AB折叠，圆弧恰好经过圆心O，∴OD=CD，∴OD= OC= OA，∴∠OAD=30°，又∵ OA=OB，∴∠OBA=30°，∴∠AOB=120°，∴∠APB= ∠AOB=60°．
活动2
探究三 例题分析
提升型例题
活动2
探究三 例题分析
例4．在⊙O中，弦AB所对圆心角为40°，则弦AB所对的圆周角为_______________．
提升型例题
【思路点拨】由⊙O的弦AB所对的圆心角为40°，根据圆周角定理与圆的内接四边形的性质，即可求得弦AB所对的圆周角的度数．
20°或160°
【解题过程】解：∵⊙O的弦AB所对的圆心角为40°， ∴弦AB所对的圆周角的度数为： ∠AOB=20°或180°﹣20°=160°．
活动2
探究三 例题分析
提升型例题
【思路点拨】首先根据题意画出图形，然后由垂径定理，求得AC的长，即可得△OAC是等腰直角三角形，则可求得∠AOB的度数，然后由圆周角定理，求得答案．
练习4：在⊙O中，若弦AB长2 cm，弦心距为 cm，则此弦所对的圆周角等于______　．
【解题过程】解：如图，连接OA，OB，则AB=2 cm，OC= cm，∵OC⊥AB，∴AC= AB= （cm），∴OC=AC，∴∠AOC=45°，∴∠AOB=90°，∴∠ADB= ∠AOB=45°，∴∠AEB=180°﹣∠ADB=135°．∴此弦所对的圆周角等于45°或135°．
活动2
探究三 例题分析
提升型例题
活动3
探究三 例题分析
例5．已知弦AB、CD相交于E， 的度数为90°， 的度数为30°，则∠AEC=_______．
探究型例题
【解题过程】解：连接BC，∵ 的度数为90°， 的度数为30°，∴∠ABC=45°，∠BCD=15°，∴∠AEC=∠ABC+∠BCD=60°．
60°
活动3
探究三 例题分析
练习5．等腰△ABC的顶角∠A=120°，腰AB=AC=10，△ABC的外接圆半径等于_______．
探究型例题
【解题过程】解：连接OA交BC与点D，连接OC，∵AB=AC，∴ = ，∴OA⊥BC又∵等腰△ABC的顶角∠A=120°∴∠BAO=∠CAO=60°，在△AOC中，又∵OA=OC∴△AOC为等边三角形∴OA=AC=10
10
知识梳理
（1）在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧和弦也相等．（2）在同圆或等圆中，等弦所对的圆周角相等或互补．（3）圆内接四边形的对角互补．
重难点突破
1.在同圆或等圆中，等弦所对的圆周角相等或互补．2.圆内接四边形的对角互补．
选择“《圆周角（2）》随堂检测 ”
点击“随堂训练→名师训练”