高中数学新教材选择性必修第一册课件+讲义 章末检测试卷(1)

这是一份数学选择性必修 第一册全册综合课前预习ppt课件，文件包含高中数学新教材选择性必修第一册章末检测试卷1pptx、高中数学新教材选择性必修第一册章末检测试卷1教师版docx、高中数学新教材选择性必修第一册章末检测试卷1学生版docx等3份课件配套教学资源，其中PPT共55页， 欢迎下载使用。

高考政策|高中“新”课程，新在哪里?
1、科目变化：外语语种增加，体育与健康必修。第一，必修课程，由国家根据学生全面发展需要设置，所有学生必须全部修习、全部考试。第二，选择性必修课程，由国家根据学生个性发展和升学考试需要设置。第三，选修课程，由学校根据实际情况统筹规划开设，学生自主选择修习。2、课程类别变化，必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下，对原必修课程学分进行重构，由必修课程学分、选择性必修课程学分组成，适当增加选修课程学分。3、学时和学分变化，高中生全年假期缩减到11周。4、授课方式变化，选课制度将全面推开。5、考试方式变化，高考统考科目由教育部命题，学业水平合格性、等级性考试由各省命题。
第一章　 空间向量与立体几何
(时间：120分钟 满分：150分)
一、单项选择题(本题共8小题，每小题5分，共40分)
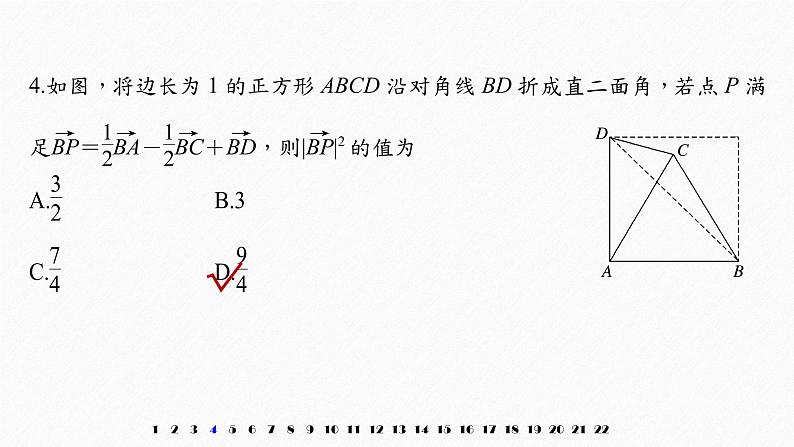
2.已知a＝(2，－1,3)，b＝(－1,4，－2)，c＝(1,3，λ)，若a，b，c三向量共面，则实数λ等于A.1 B.2 C.3 D.4
解析　若向量a，b，c共面，则c＝xa＋yb，其中x，y∈R，即(1,3，λ)＝(2x，－x,3x)＋(－y,4y，－2y)＝(2x－y，－x＋4y,3x－2y)，
3.若向量a＝(x,4,5)，b＝(1，－2,2)，且a与b的夹角的余弦值为 则x等于A.3 B.－3 C.－11 D.3或－11
解析　因为a·b＝(x,4,5)·(1，－2,2)＝x－8＋10＝x＋2，
解得x＝3或x＝－11(舍去).
5.已知空间向量a＝(1，n,2)，b＝(－2,1,2)，若2a－b与b垂直，则|a|等于
解析　因为a＝(1，n,2)，b＝(－2,1,2)，所以2a－b＝(4,2n－1,2).因为2a－b与b垂直，所以(2a－b)·b＝0，所以－8＋2n－1＋4＝0，
6.如图所示，在空间直角坐标系中，BC＝4，原点O是BC的中点，点 点D在平面Oyz内，且∠BDC＝90°，∠DCB＝30°，则AD的长为
解析　因为点D在平面Oyz内，所以点D的横坐标为0，又BC＝4，原点O是BC的中点，∠BDC＝90°，∠DCB＝30°，
纵坐标y＝－(2－4·sin 30°·cs 60°)＝－1，
7.如图，在四棱锥P－ABCD中，底面ABCD为直角梯形，AB⊥AD，BC∥AD，且AB＝BC＝2，AD＝3，PA⊥平面ABCD且PA＝2，则PB与平面PCD所成角的正弦值为
解析　依题意，以A为坐标原点，分别以AB，AD，AP为x，y，z轴建立空间直角坐标系，AB＝BC＝2，AD＝3，PA＝2，则P(0,0,2)，B(2,0,0)，C(2,2,0)，D(0,3,0)，
设平面PCD的法向量为n＝(a，b，c)，
不妨取c＝3，则a＝1，b＝2，所以平面PCD的一个法向量为n＝(1,2,3)，所以PB与平面PCD所成角的正弦值为
8.已知四棱锥P－ABCD，底面是边长为2的正方形，△PAD是以AD为斜边的等腰直角三角形，AB⊥平面PAD，点E是线段PD上的动点(不含端点)，若线段AB上存在点F(不含端点)，使得异面直线PA与EF成30°的角，则线段PE长的取值范围是
解析　由△PAD是以AD为斜边的等腰直角三角形，AB⊥平面PAD，取AD中点G，建立如图所示的空间直角坐标系，依题意G(0,0,0)，A(1,0,0)，D(－1，0,0)，B(1,2,0)，P(0,0,1)，设F(1，y,0)，
A.(4，－2,2) B.(－2,2,4)C.(－4,2，－2) D.(2，－2,4)
二、多项选择题(本大题共4小题，每小题5分，共20分，全部选对的得5分，部分选对的得2分，有选错的得0分)
故点P的坐标为(4，－2,2)或(－2,2,4).
10.如图，在棱长为2的正方体ABCD－A1B1C1D1中，E，F分别是DD1，DB的中点，则下列选项中正确的是A.EF∥平面ABC1D1B.EF⊥B1CC.EF与AD1所成角为60°D.EF与平面BB1C1C所成角的正弦值为
解析　连接BD1(图略)，∴EF∥BD1，得EF∥平面ABC1D1，故A正确；∵B1C⊥BC1，又由D1C1⊥平面BCC1B1，得B1C⊥D1C1，∴B1C⊥平面BD1C1.∵BD1⊂平面BD1C1，∴B1C⊥BD1.又∵BD1∥EF，∴EF⊥B1C，故B正确；
且△AD1B为直角三角形，
∵EF∥BD1，又D1C1⊥平面BB1C1C，∴∠D1BC1即为EF与平面BB1C1C所成角，
11.如图所示，在直三棱柱ABC－A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC＝2a，BB1＝3a，D是A1C1的中点，点E在棱AA1上，要使CE⊥平面B1DE，则AE的值可能是
解析　以B为坐标原点，BA，BC，BB1所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，
由CE⊥平面B1DE，得CE⊥DE，CE⊥B1E，
解得z＝a或2a，即AE＝a或2a.
12.将正方形ABCD沿对角线BD翻折，使平面ABD与平面BCD的夹角为90°，以下四个结论正确的是A.AC⊥BDB.△ACD是等边三角形C.直线AB与平面BCD所成的角为D.AB与CD所成的角为
解析　如图所示，以BD中点O为坐标原点，OD，OA，OC所在直线分别为x轴、y轴、z轴，建立空间直角坐标系Oxyz，
则D(1,0,0)，B(－1,0,0)，C(0,0,1)，A(0,1,0)，
故AC⊥BD，A正确；
所以△ACD为等边三角形，B正确；
解析　∵a＝(－2,1,3)，b＝(－1,2,1)，
三、填空题(本题共4小题，每小题5分，共20分)13.已知a＝(－2,1,3)，b＝(－1,2,1)，a与b夹角的余弦值为______.
解析　根据题意可知，当VD－ABC最大时，平面DAC⊥平面ABC，设AC的中点为O，连接OB，OD建立空间直角坐标系，如图所示，令OB＝OC＝OD＝1，则O(0,0,0)，A(0，－1,0)，D(0,0,1)，B(1,0,0)，C(0,1,0)，
14.将正方形ABCD沿对角线AC折起，当以A，B，C，D四点为顶点的三棱锥体积最大时，异面直线AD与BC所成的角为____.
解析　建立如图所示的空间直角坐标系，则D(0,0,0)，A(1，－1,0)，B(1,0,0)，C(0,1,0)，C1(0,1,2)，
设平面EDC1的法向量为n＝(x，y，z)，
16.如图，正方形ABCD，ABEF的边长都是1，而且平面ABCD，ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM＝BN＝a(0解析　建立空间直角坐标系如图，则A(1,0,0)，F(1,1,0)，C(0,0,1).
17.(10分)已知a＝(x,4,1)，b＝(－2，y，－1)，c＝(3，－2，z)，a∥b，b⊥c，求：(1)a，b，c；
四、解答题(本大题共6小题，共70分)
解得x＝2，y＝－4，则a＝(2,4,1)，b＝(－2，－4，－1).又b⊥c，所以b·c＝0，即－6＋8－z＝0，解得z＝2，于是c＝(3，－2,2).
解　由(1)得a＋c＝(5,2,3)，b＋c＝(1，－6,1)，设a＋c与b＋c的夹角为θ，
(2)a＋c与b＋c夹角的余弦值.
18.(12分)如图所示，在四棱锥P－ABCD中，PC⊥平面ABCD，PC＝2，在四边形ABCD中，CD∥AB，∠ABC＝∠BCD＝90°，AB＝4，CD＝1，点M在PB上，且PB＝4PM，∠PBC＝30°，求证：CM∥平面PAD.
证明　建立如图所示的空间直角坐标系Cxyz，∵∠ PBC＝30°，PC＝2，
设平面PAD的一个法向量为n＝(x，y，z)，
19.(12分)如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB＝AD＝2，CD＝4，M为CE的中点.(1)求证：BM∥平面ADEF；
证明　∵平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD＝AD，AD⊥ED，ED⊂平面ADEF，∴ED⊥平面ABCD.
则D(0,0,0)，A(2,0,0)，B(2,2,0)，C(0,4,0)，E(0,0,2)，F(2,0,2).
∵M为EC的中点，∴M(0,2,1)，
又BM⊄平面ADEF，∴BM∥平面ADEF.
(2)求证：BC⊥平面BDE.
又DE∩DB＝D，DE，DB⊂平面BDE，∴BC⊥平面BDE.
20.(12分)在三棱柱ABC－A1B1C1中，底面ABC为正三角形，且侧棱AA1⊥底面ABC，且底面边长与侧棱长都等于2，O，O1分别为AC，A1C1的中点，求平面AB1O1与平面BC1O间的距离.
解　如图，连接OO1，根据题意，OO1⊥底面ABC，则以O为原点，分别以OB，OC，OO1所在的直线为x，y，z轴建立空间直角坐标系.∵AO1∥OC1，OB∥O1B1，AO1∩O1B1＝O1，OC1∩OB＝O，∴平面AB1O1∥平面BC1O.∴平面AB1O1与平面BC1O间的距离即为点O1到平面BC1O的距离.
设n＝(x，y，z)为平面BC1O的法向量，
∴可取n＝(0,2，－1).点O1到平面BC1O的距离记为d，
21.(12分)如图，在四棱锥P－ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点.(1)求证：BE⊥DC；
证明　依题意，以点A为坐标原点建立空间直角坐标系(如图)，可得A(0,0,0)，B(1,0,0)，C(2,2,0)，D(0,2,0)，P(0,0,2).由E为棱PC的中点，得E(1,1,1)，
(2)若F为棱PC上一点，满足BF⊥AC，求平面FAB与平面ABP夹角的余弦值.
设n1＝(x，y，z)为平面FAB的法向量，
不妨令z＝1，可得n1＝(0，－3,1)为平面FAB的一个法向量.易知向量n2＝(0,1,0)为平面ABP的一个法向量，
22.(12分)在Rt△ABC中，∠C＝90°，AC＝4，BC＝2，E是AC的中点，F是线段AB上一个动点， (0<λ<1)，如图所示，沿BE将△CEB翻折至△DEB的位置，使得平面DEB⊥平面ABE.
证明　在△ABC中，∠C＝90°，即AC⊥BC，则BD⊥DE，取BF的中点N，连接CN交BE于点M，
∴EF是△ANC的中位线，∴EF∥CN.在△BEF中，N是BF的中点，∴M是BE的中点，在Rt△BCE中，EC＝BC＝2，∴CM⊥BE，则EF⊥BE.
又平面DEB⊥平面ABE，平面DEB∩平面ABE＝BE，EF⊂平面ABE，∴EF⊥平面DEB.又BD⊂平面BDE，∴EF⊥BD.而EF∩DE＝E，EF，DE⊂平面DEF，∴BD⊥平面DEF.
以C为坐标原点，CA所在直线为x轴，CB所在直线为y轴，建立如图所示的空间直角坐标系.则C(0,0,0)，A(4,0,0)，B(0,2,0)，E(2,0,0)
取BE的中点G，连接DG，则DG⊥BE，而平面DEB⊥平面ABC，