湖北省武汉市常青第一中学2022-2023学年八年级下学期三月月考数学试卷(含解析)

这是一份湖北省武汉市常青第一中学2022-2023学年八年级下学期三月月考数学试卷(含解析)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
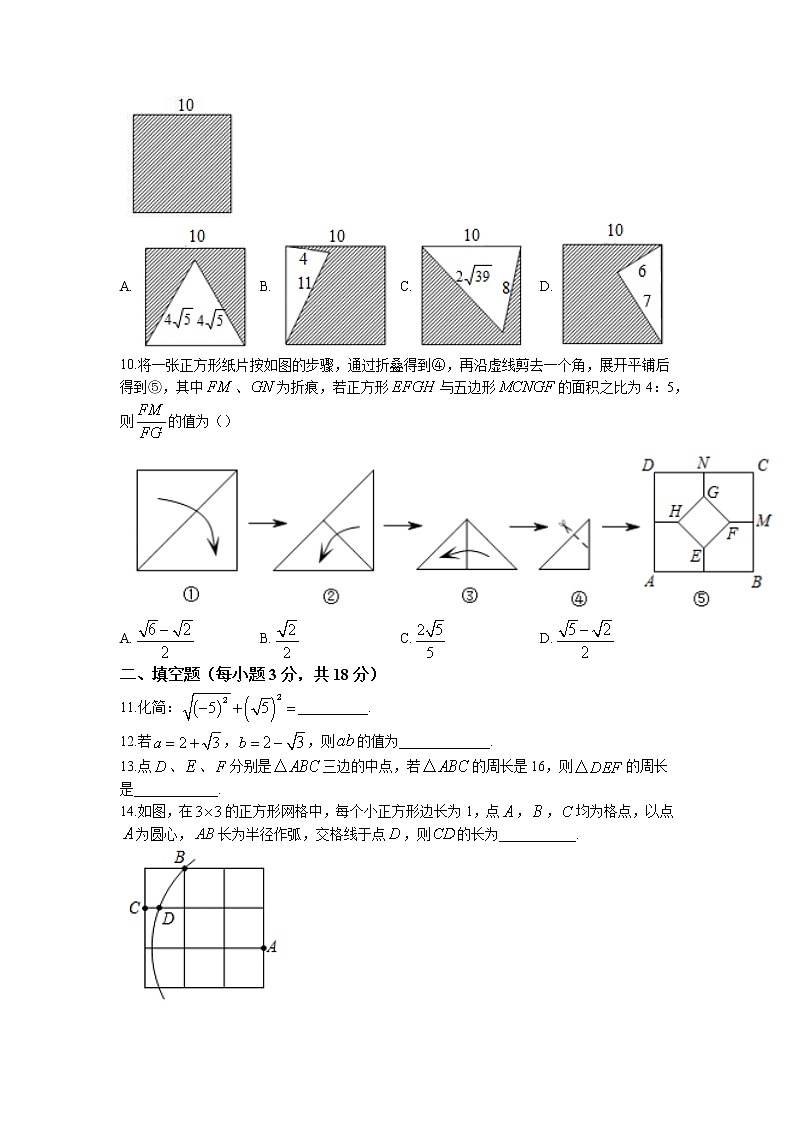
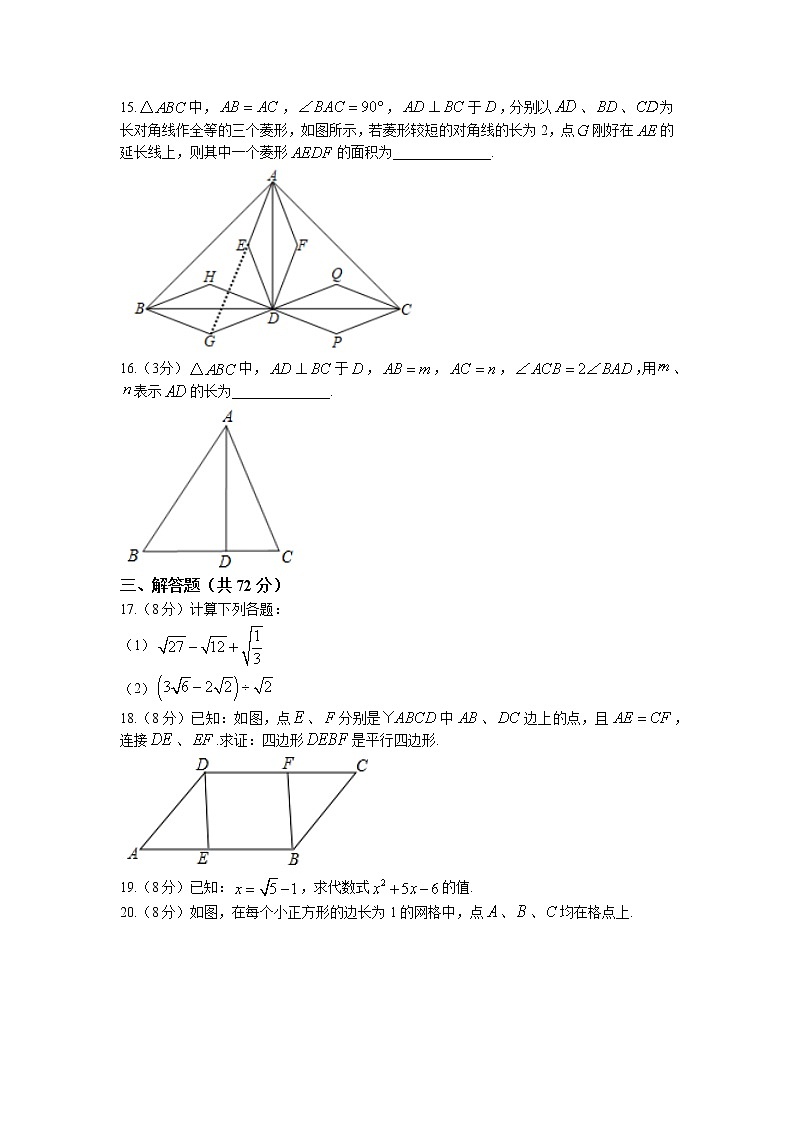
武汉市常青第一学校八年级三月月考数学试卷一、选择题（每小题3分，共30分）1.下列式子中，属于最简二次根式的是（）A. B. C. D.2.使二次根式有意义的的取值范围是（）A. B. C. D.3.下列计算正确的是（）A. B. C. D.4.下列各组数中，以、、为边的三角形不是直角三角形的是（）A.，， B.，，C.，， D.，，5.在平行四边形中，比大40°，那么的度数为（）A.60° B.70° C.80° D.110°6.在下列给出的条件中，能判定四边形为平行四边形的是（）A.， B.，C.， D.，7.如图，正方体的棱长为2，为一条棱的中点.已知蚂蚁沿正方体的表面从点出发，到达点，则它运动的最短路程为（）A. B.4 C. D.58.菱形的边长为2，点为的中点，以为边作菱形，其中点在的延长线上，点为的中点，则（）A. B. C. D.9.将一个边长为10的正方形铁片，过两个顶点剪掉一个三角形，以下四个剪法中，裁剪线的长度所标的数据不可能的是（）A. B. C. D.10.将一张正方形纸片按如图的步骤，通过折叠得到④，再沿虚线剪去一个角，展开平铺后得到⑤，其中、为折痕，若正方形与五边形的面积之比为4：5，则的值为（）A. B. C. D.二、填空题（每小题3分，共18分）11.化简：__________.12.若，，则的值为_____________.13.点、、分别是三边的中点，若的周长是16，则的周长是____________.14.如图，在的正方形网格中，每个小正方形边长为1，点，，均为格点，以点为圆心，长为半径作弧，交格线于点，则的长为___________.15.中，，，于，分别以、、为长对角线作全等的三个菱形，如图所示，若菱形较短的对角线的长为2，点刚好在的延长线上，则其中一个菱形的面积为______________.16.（3分）中，于，，，，用、表示的长为______________.三、解答题（共72分）17.（8分）计算下列各题：（1）（2）18.（8分）已知：如图，点、分别是中、边上的点，且，连接、.求证：四边形是平行四边形.19.（8分）已知：，求代数式的值.20.（8分）如图，在每个小正方形的边长为1的网格中，点、、均在格点上.（1）直接写出的长为________，的面积为____________；（2）请在如图所示的网格中，用无刻度的直尺作出边上的高，并保留作图痕迹；（3）求的长.21.已知：如图，在中，，是的角平分线，，，求的长.22.（10分）在中，.（1）若，点、在、上，将沿折叠，使得点与点重合，求折痕的长；（2）点在的延长线上，且，若，求证：是直角三角形.23.（10分）中，点、分别在、上，，.（1）当时，求证：为等边三角形；（2）当时，求证：；（3）当，，时，直接写出线段的长为___________.24.（12分）已知，点P为射线上任意一点（点P与点B不重合），分别以、为边在的内部作等边和，连接并延长交于点（1）如图1，若，点A、E、P恰好在一条直线上时，求此时的长（直接写出结果）（2）如图2，当点P为射线上任意一点时，猜想与图中的哪条线段相等（不能添加辅助线产生新的线段），并加以证明（3）若，设，求的长参考答案与试题解析一、选择题（每小题3分，共30分）1.（3分）【分析】根据最简二次根式满足的条件对各选项进行判断.【解答】解：，，，只有为最简二次根式.故选：B.【点评】本题考查了最简二次根式：把满足下述两个条件的二次根式，叫做最简二次根式，（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式.2.（3分）【分析】利用当二次根式有意义时，被开方式为非负数，得到有关的一元一次不等式，解之即可得到本题答案.【解答】解：二次根式有意义，，解得：，故选：D.【点评】本题考查了二次根式有意义的条件，此类考题相对比较简单，但从近几年的中考看，几乎是一个必考点.3.（3分）【分析】先把各个二次根式化成最简二次根式再合并判断即可.【解答】解：A、，错误，不符合题意；B、，错误，不符合题意；C、，正确，符合题意；D、，错误，不符合题意；故选：C.【点评】此题考查二次根式的加减，关键是先把各个二次根式化成最简二次根式再合并解答.4.（3分）【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可.如果有这种关系，就是直角三角形，没有这种关系，就不是直角三角形.【解答】解：A、，符合勾股定理的逆定理，是直角三角形，故此选项错误；B、，符合勾股定理的逆定理，是直角三角形，故此选项错误；C、，不符合勾股定理的逆定理，不是直角三角形，故此选项正确；D、，符合勾股定理的逆定理，是直角三角形，故此选项错误.故选：C.【点评】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断.5.（3分）【分析】根据平行四边形的对角相等，邻角之和为180°，即可求出该平行四边形各个内角的度数.【解答】解：画出图形如下所示：四边形是平行四边形，，，又，，，.故选：D.【点评】本题考查平行四边形的性质，解题关键是掌握平行四边形的对角相等，邻角之和为180°，难度一般.6.（3分）【分析】根据平行四边形的判定进行判断即可得出结论.【解答】解：如图所示，根据平行四边形的判定，A、B、D条件均不能判定为平行四边形，C选项中，由于，，所以，所以只有C能判定.故选：C.【点评】平行四边形的判定方法共有五种，在四边形中如果有：1、四边形的两组对边分别平行；2、一组对边平行且相等；3、两组对边分别相等；4、对角线互相平分；5、两组对角分别相等.则四边形是平行四边形.7.（3分）【分析】正方体侧面展开为长方形，确定蚂蚁的起点和终点，根据两点之间线段最短，根据勾股定理可求出路径长，【解答】解：如图，它运动的最短路程，故选：C.【点评】本题考查平面展开最短路径问题，关键是知道两点之间线段最短，找到起点终点，根据勾股定理求出.8.（3分）【分析】连接、，根据菱形的边长为2，可得，由，可得是等边三角形，进而可求，再根据勾股定理分别求出、的长，进而可得的长.【解答】解：如图，连接、，菱形的边长为2，，，是等边三角形，，，，点为的中点，菱形的边长为1，即，点在的延长线上，，，连接，于点，，，，根据勾股定理，得，点为的中点，.故选：A.【点评】本题考查了菱形的性质、等边三角形的判定与性质、直角三角形斜边上的中线、勾股定理，解决本题的关键是掌握菱形的性质.9.（3分）【分析】直接验证三角形三边的平方之间的关系即可作出判断.【解答】解：对于A选项，，三角形为锐角三角形，合理；对于B选项，，说明边长为11的边所对的角是钝角，这个时候三角形不可能完全处在正方形内，故不合理；对于C选项，，且，三角形为锐角三角形，合理；对于D选项，，说明边长为10的边所对的角为钝角，合理.故选：B.【点评】本题主要考查了正方形的性质和勾股定理.正确判断各三角形的形状是解答的关键.10.（3分）【分析】连接，直线与交于点，根据正方形与五边形的面积之比为4：5，设正方形与五边形的面积为，，可得，根据折叠可得正方形的面积为，进而求出，最后求得结果.【解答】解：如图，连接，直线与交于点，正方形与五边形的面积之比为，设正方形与五边形的面积为，，，，，由折叠可知：正方形的面积为：，，.故选：A.【点评】本题考查了剪纸问题，解决本题的关键是掌握对称的性质.二、填空题（每小题3分，共18分）11.（3分）答案：10【分析】根据二次根式的性质计算.【解答】解：原式.【点评】本题考查了二次根式的混合运算：在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍.12.（3分）答案：1【分析】直接利用平方差公式计算得出答案.【解答】解：，，.故答案为：1.【点评】此题主要考查了二次根式的化简求值，正确运用乘法公式是解题关键.13.（3分）答案：8【解答】解：如图，、、分别是、、的中点，、、为中位线，，，；，故答案为：8.【点评】本题考查了三角形的中位线定理，根据中点判断出中位线，再利用中位线定理是解题的基本思路.14.（3分）答案：【分析】由勾股定理求出，再由勾股定理求出，即可得出的长.【解答】解：连接，，如图所示：，.故答案为：.【点评】本题考查了勾股定理，由勾股定理求出，是解决问题的关键.15.（3分）答案：【分析】如图所示，连接，设交于点，先证明是等腰直角三角形，再证明，从而在中，由勾股定理得，求得的值，再根据菱形的面积等于底乘以高，得出菱形的面积，即菱形的面积.
【解答】解：如图所示，连接，设交于点，则，三个菱形全等，，，于，，是等腰直角三角形，，四边形为菱形，，，，，设，则，，在中，由勾股定理得：，解得：，菱形的面积为：，菱形的面积为：.故答案为：.【点评】本题考查了菱形的性质、菱形的面积计算、等腰直角三角形的判定及勾股定理在计算中的应用，明确菱形的性质及根据勾股定理构建方程是解题的关键.16.（3分）答案：【分析】延长至，使，连接，根据三角形的外角性质、等腰三角形的性质得到，得到，根据勾股定理、三角形的面积公式计算即可.【解答】解：延长至，使，连接，则，，，，，即，，，，，，由勾股定理得，，，即，解得，，故答案为：.【点评】本题考查的是等腰三角形的性质、直角三角形的性质、勾股定理，掌握三角形的外角性质、灵活运用三角形的面积公式是解题的关键.三、解答题（共72分）17.（8分）【分析】（1）先把二次根式化为最简二次根式，然后合并即可；（2）根据二次根式的除法法则运算.【解答】解：（1）原式（2）原式.【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可.在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍.18.（8分）【分析】利用平行四边形的性质得出，，进而求出，进而利用一组对边平行且相等的四边形是平行四边形进而求出即可.【解答】证明：在中，则，，，，四边形是平行四边形.【点评】此题主要考查了平行四边形的判定与性质，得出是解题关键.19.（8分）【分析】把的值代入多项式进行计算即可.【解答】解：当，.【点评】本题考查了二次根式的化简求值，掌握完全平方公式是解题的关键.20.（8分）【分析】（1）根据勾股定理和三角形的面积公式即可得到结论；（2）根据题意画出线段即可；（3）根据三角形的面积公式即可得到结论.【解答】解：（1），，故答案为，9；（2）如图所示，即为所求，（3），.【点评】本题考查了作图-应用与设计作图，三角形的面积的计算，勾股定理，正确的作出图形是解题的关键.21.（8分）22.（10分）【分析】（1）如图1，过作于，根据等腰三角形的性质得到，求得，根据折叠的性质得到，，设，根据勾股定理即可得到结论；（2）如图2，过作于，根据等腰三角形的性质得到，设，，，得到，根据勾股定理和勾股定理的逆定理即可得到结论.【解答】解：（1）如图1，过作于，，，，，将沿折叠，使得点与点重合，，，设，，，，解得：，；（2）如图2，过作于，，设，，，，，，，联立方程组解得，（负值舍去），，，是直角三角形.【点评】本题考查了翻折变换（折叠问题），等腰三角形的性质，勾股定理的逆定理，勾股定理，正确的作出辅助线构造直角三角形是解题的关键.23.（10分）【分析】（1）根据菱形的判定定理得到平行四边形为菱形，得到为等边三角形，证明，根据全等三角形的性质得到，根据等边三角形的判定定理证明结论；（2）延长至，使，延长至，使，延长、交于点，根据菱形的判定定理得到四边形为平行四边形，根据（1）中结论解答；（3）延长交的延长线于，延长交的延长线于，作于，把绕点顺时针旋转120°，得到，求出的长，证明，根据全等三角形的性质得到，得到答案.【解答】（1）证明：当时，，平行四边形为菱形，，，为等边三角形，，，，，在和中，，，又，为等边三角形；（2）证明：如图2，延长至，使，延长至，使，延长、交于点，，是的中位线，，又，四边形为平行四边形，平行四边形为菱形，由（1）可知，为等边三角形，；（3）解：如图3，延长交的延长线于，延长交的延长线于，作于，把绕点顺时针旋转120°，得到，，，，，又，，在中，，，由勾股定理得，，，，同理，，，，，，，由勾股定理得，，，，，，，即，，在和中，，故答案为：.【点评】本题考查的是菱形的判定和性质、全等三角形的判定和性质、等边三角形的性质、旋转变换的应用，正确作出辅助线、掌握全等三角形的判定定理和性质定理是解题的关键.