

所属成套资源:【期中必备】2022-2023学年度人教版五年级数学下册期中易错题+真题演练(含答案)
3.长方体和正方体(拔高版)-2022-2023学年五年级下册数学期中专项复习(人教版)
展开
这是一份3.长方体和正方体(拔高版)-2022-2023学年五年级下册数学期中专项复习(人教版),共18页。
3.长方体和正方体(拔高版)
2022-2023学年五年级下册数学期中专项复习
【知识梳理】
一、长方体和正方体的特征。
1、长方体的特征:长方体是由6个长方形(特殊情况下由2个相对的面是正方形)围成的立体图形。长方体有6个面,相对的面完全相同;有12条棱,相对的棱长度相等;有8个顶点。
2、相交与一个顶点的3条棱的长度分别叫作长方体的长、宽、高,长方体的12条棱中有4条长、4条宽和4调高。
3、正方体是又6个完全相同的正方形围成的立体图形。正方形有12条棱,每条棱的长度都相等;正方体有8个顶点。
4、正方体可以堪称长、宽、高都相等的长方体。正方体是特殊的长方体。
二、长方体和正方体的表面积。
1、长方体或正方体6个面的总面积,叫作它的表面积。
2、长方体的表面积的计算公式。
(1)长方体的表面积=长×宽×2+长×高×2+宽×高×2,用公式表示S=2ab+2ah+2bh。
(2)长方体的表面积=(长×宽+长×高+宽×高)×2,用公式表示S=2(ab+ah+bh)。
注意:S表示长方体的表面积,a,b,h分别表示长方体的长、宽、高。
3、正方体的表面积的计算公式:正方体的表面积=棱长×棱长×6,用字母表示是S=6a2,其中S表示正方体的表面积,a表示正方体的棱长。
三、长方体和正方体的体积。
1、体积的意义。
物体所占空间的大小叫作物体的体积。
2、常用的体积单位。
常用的体积单位:立方米(m3)、立方分米(dm3)、立方厘米(cm3)。
3、长方体的体积计算公式。
长方体的体积=长×宽×高,用字母表示为V=abh。
4、长方体的体积计算公式。
正方体的体积=棱长×棱长×棱长,用字母表示为V=a3。
5、长方体和正方体的体积计算公式的应用。
已知长方体(正方体)的长宽高(棱长),根据长方体的体积公式或正方体的体积公式可直接求出长方体(正方体)的体积。
6、每相邻的两个体积但未见的进率是1000。1米3=1000分米3,1分米3=1000厘米3。
7、体积单位间的换算方法:把高级单位的名数换算成低级单位的名数,用高级单位的数乘进率;把低级单位的名数换算成高级单位的名数,用低级单位的数除以进率。
8、容积的意义:容器所能容纳物体的体积,通常叫做它的容积。
9、容积单位:计量物体的容积,常用体积单位。计量液体的体积常用升和毫升作单位。
10、1升=1000毫升,1升=1分米3,1毫升=1厘米3。
11、测量不规则物体的体积可以用排水法。利用有刻度的量杯记录下放入不规则物体前后水位的刻度,上升的那部分水的体积就是不规则物体的体积。
【专项练习】
一、选择题(每题2分,共10分)
1.图中,每个小正方体的体积是1dm3,大长方体的体积是( )。
A.20dm3 B.30dm3 C.36dm3 D.45dm3
2.一瓶矿泉水是500毫升,每人每天约需要2.5升水,10万人每天大约需要( )瓶矿泉水。
A.5万 B.50万 C.500万 D.5000万
3.一个长方体的棱长之和是720cm,左面图形的周长是180cm,前面图形的周长是260cm,它的长、宽、高是 ( )cm。
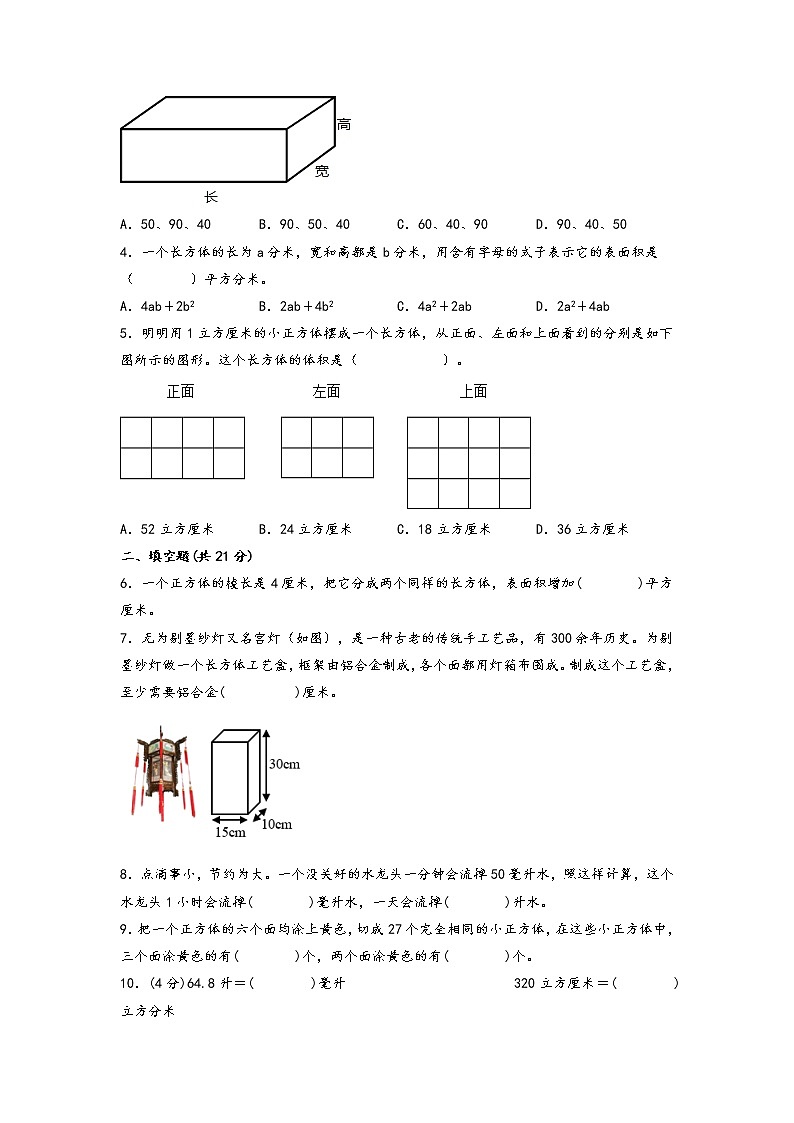
A.50、90、40 B.90、50、40 C.60、40、90 D.90、40、50
4.一个长方体的长为a分米,宽和高都是b分米,用含有字母的式子表示它的表面积是( )平方分米。
A.4ab+2b2 B.2ab+4b2 C.4a2+2ab D.2a2+4ab
5.明明用1立方厘米的小正方体摆成一个长方体,从正面、左面和上面看到的分别是如下图所示的图形。这个长方体的体积是( )。
A.52立方厘米 B.24立方厘米 C.18立方厘米 D.36立方厘米
二、填空题(共21分)
6.一个正方体的棱长是4厘米,把它分成两个同样的长方体,表面积增加( )平方厘米。
7.无为剔墨纱灯又名宫灯(如图),是一种古老的传统手工艺品,有300余年历史。为剔墨纱灯做一个长方体工艺盒,框架由铝合金制成,各个面都用灯箱布围成。制成这个工艺盒,至少需要铝合金( )厘米。
8.点滴事小,节约为大。一个没关好的水龙头一分钟会流掉50毫升水,照这样计算,这个水龙头1小时会流掉( )毫升水,一天会流掉( )升水。
9.把一个正方体的六个面均涂上黄色,切成27个完全相同的小正方体,在这些小正方体中,三个面涂黄色的有( )个,两个面涂黄色的有( )个。
10.(4分)64.8升=( )毫升 320立方厘米=( )立方分米
37.03立方米=( )立方分米 76立方厘米=( )毫升
11.(3分)一个长方体框架,长,宽,高,做这个框架至少要( )的铁丝;若在框架四周和底部围上铁皮,至少需要( )的铁皮,围上铁皮后在里面最多能装( )水。(铁皮的厚度忽略不计)
12.(3分)一个正方体的棱长总和是48分米,它的棱长是( )分米,表面积是( )平方分米,体积是( )立方分米。
13.用丝带捆扎一种礼品盒(如图),结头长15厘米,要捆扎这种礼品盒,至少需要准备( )分米长的丝带。
14.(3分)
(1)从正面看,形状是的有( );从上面看,形状是的有( )。(填序号)。
(2)如果要将④摆成一个较大的正方体,至少还需要( )个相同的小正方体。
15.一根3米长的长方体钢材,沿横截面切成两段后,表面积增加了0.8平方米,这段钢材原来的体积是( )。
三、判断题(每题1分,共5分)
16.用8个大小相同的小正方体拼成一个大正方体,如果拿走其中一个小正方体,它的表面积不变。( )
17.一个长方体长、宽、高同时扩大到原来的2倍,那么它的棱长总和扩大到原来的6倍。( )
18.一个正方体的棱长总和是72厘米,它的体积和表面积相等。( )
19.表面积相等的两个正方体,体积也相等。( )
20.底面周长是8cm的正方体,体积是8cm3。( )
四、计算题(共12分)
21.(6分)计算下面图形的体积。
(1)(2)
22.(6分)分别求出下面图形的表面积和体积。
五、作图题(共4分)
23.(4分)请把下图补充成完整的正方体展开图。
六、解答题(共48分)
24.(6分)一块长方形纸板,长30厘米,宽25厘米,像下图那样,从四角各剪去一个边长为5厘米的正方形,再做成无盖的长方体盒子。这个盒子的容积是多少立方厘米?(纸板到厚度忽略不计)
25.(6分)一个正方体纸箱的棱长是20厘米,如果围着它贴一圈商标纸(上、下面不贴),至少需要多少平方厘米的商标纸?
26.(6分)用下面五块玻璃(如图)可以拼接成一个无盖的长方体玻璃容器(接头处忽略不计)。现将500毫升水倒入这个容器中,水面高多少厘米?(单位:厘米)
27.(6分)把一个边长30厘米的正方形硬纸板的四个角各剪去一个边长4厘米的正方形,做一个无盖的长方体纸盒。这个纸盒容积是多少毫升?(纸板厚度不计)
28.(6分)一个正方体容器,从里面量棱长为2分米,倒入5L水,再把一块石头没入水中。这时量得容器内水深1.5分米。石头的体积是多少立方分米?
29.(6分)家具厂订购500根方木,每根方木横截面的面积是2.4平方分米,长是3米。这批木料一共有多少方(立方米)?如果收购价是800元/方,这批木料要花多少钱?
30.(6分)有两根同样长的铁丝,一根围成了一个长9厘米,宽6厘米,高6厘米的长方体,另一根则围成了一个正方体。
(1)围成的正方体的棱长是多少厘米?
(2)在这个正方体的四周和底面贴上彩纸,需要多少平方厘米的彩纸?
31.(6分)一个长方体的玻璃缸,长8分米,宽5分米,高4分米,向其中倒入120升水。如果投入一个棱长为4分米的正方体铁块,缸内的水会溢出么?如溢出会溢出多少升?
参考答案
1.D
【分析】通过观察图形可知,沿长方体的长摆了5个小正方体,沿宽摆了3行,沿高摆了3层,根据长方体的体积=长×宽×高,求出一共摆了多少个小正方体,然后再乘每个小正方体的体积即可。
【详解】1×(5×3×3)
=1×(15×3)
=1×45
=45(dm3)
大长方体的体积是45dm3。
故答案为:D
【点睛】此题考查的目的是理解掌握长方体体积公式的推导过程及应用。
2.B
【分析】根据1升=1000毫升,先将500毫升化为0.5升,再根据除法的意义,用2.5÷0.5即可求出每人每天需要的矿泉水瓶数,再乘10即可求出10万人每天大约需要的瓶数。
【详解】500毫升=0.5升
2.5÷0.5×10
=5×10
=50(万瓶)
10万人每天大约需要50万瓶矿泉水。
故答案为:B
【点睛】本题考查了容积单位的换算以及小数除法的应用。
3.B
【分析】根据长方体的棱长总和=(长+宽+高)×4,据此求出长、宽与高的和;再根据长方形的周长公式:C=(a+b)×2,据此求出左面和前面图形长与宽的和,进而求出该长方体的长、宽和高。
【详解】720÷4=180(厘米)
180÷2=90(厘米)
260÷2=130(厘米)
180-90=90(厘米)
180-130=50(厘米)
130-90=40(厘米)
则这个长方体的长、宽、高分别是90厘米,50厘米,40厘米。
故答案为:B
【点睛】本题考查长方体的总棱长,求出该长方体的长、宽与高的和是解题的关键。
4.A
【分析】根据长方体表面积公式:长方体的表面积=(长×宽+长×高+宽×高)×2,用(a×b+a×b+b×b)×2,即可求出长方体的表面积,再化简。
【详解】(a×b+a×b+b×b)×2
=(ab+ab+b2)×2
=(2ab+b2)×2
=(4ab+2b2)平方分米
长方体的表面积是(4ab+2b2)平方分米。
故答案为:A
【点睛】本题考查了长方体表面积公式的应用以及用字母表示数。
5.B
【分析】这个立体图形从正面看,有8个小正方体,结合从左面和上面看到的图形,要摆成一个长方体,这个立体图形的摆法如下:,如图共有24个小正方体组合而成,一个小正方体的体积是1立方厘米,乘24即可求出这个长方体的体积。
【详解】根据分析得,这个长方体是由24个小正方体组合而成。
1×24=24(立方厘米)
即这个长方体的体积是24立方厘米。
故答案为:B
【点睛】利用从不同的方向观察得到的图形,根据三视图确定几何体的摆法,从而求出长方体的体积。
6.32
【分析】将一个正方体分成两个完全相同的长方体,需要切一刀,增加两个面的面积,每一个面的面积为4×4=16平方厘米。
【详解】2×(4×4)
=2×16
=32(平方厘米)
表面积增加32平方厘米。
【点睛】明确切一刀会增加两个面是解题的关键。
7.220
【分析】根据长方体的棱长和公式:长方体棱长和=(长+宽+高)×4,用(15+10+30)×4即可求出铝合金的总长度。
【详解】(15+10+30)×4
=55×4
=220(厘米)
至少需要铝合金220厘米。
【点睛】本题考查了长方体棱长和公式的灵活应用。
8. 3000 72
【分析】根据1小时=60分,用60分乘每分钟流掉水的毫升数,即可求出1小时流掉多少毫升水,一天是24小时,乘1小时流掉的毫升数,即可求出一天流掉多少毫升,根据1升=1000毫升,进行单位换算即可。
【详解】1小时=60分
60×50=3000(毫升)
3000×24=72000(毫升)
72000毫升=72升
所以,这个水龙头1小时会流掉3000毫升水,一天会流掉72升水。
【点睛】本题考查两位数乘两位数的计算及应用。理解题意,找出数量关系,列式计算即可。
9. 8 12
【分析】因为一个正方体切成27个完全相同的小正方体,根据正方体的体积V=a3可知,每条棱上有3个小正方体。正方体的特征:正方体有6个面、12条棱、8个顶点。
三面涂黄色的小正方体位于各顶点处,共有8个顶点,所以三面涂黄色的小正方体有8个。
两面涂黄色的小正方体位于每条棱上,根据两面涂黄色的小正方体个数=(每条棱上的小正方体个数-2)×12,即是两面涂黄色的小正方体的个数。
【详解】3×3×3=27
所以正方体的每条棱上有3个小正方体。
三个面涂黄色的在顶点处,所以一共有8个三个面涂黄色的小正方体。
两个面涂色的有:
(3-2)×12
=1×12
=12(个)
三个面涂黄色的有8个,两个面涂黄色的有12个。
【点睛】本题考查正方体涂色问题,掌握正方体的特征,明确三面涂色的在顶点处,两面涂色的在每条棱上。
10. 64800 0.32 37030 76
【分析】根据1升=1000毫升,1立方分米=1000立方厘米,1立方米=1000立方分米,1毫升=1立方厘米,高级单位化低级单位要乘进率,低级单位化高级单位要除以进率,据此解答。
【详解】64.8升=64800毫升
320立方厘米=0.32立方分米
37.03立方米=37030立方分米
76立方厘米=76毫升
【点睛】本题考查了体积(容积)单位的换算,明确高级单位化低级单位要乘进率,低级单位化高级单位要除以进率。
11. 180 700 1.5
【分析】根据长方体的总棱长公式:L=(a+b+h)×4,据此代入数值即可求出铁丝的长度;求铁皮的面积就是求长方体五个面的面积,根据S=(ah+bh)×2+ab,据此进行计算即可;再根据长方体的容积公式:V=abh,据此可求出最多能装多少升的水。
【详解】
(30+10+5)×4
=45×4
=180(cm)
(30×5+10×5)×2+30×10
=(150+50)×2+300
=200×2+300
=400+300
=700(cm2)
=300×5
=1500(cm3)
则做这个框架至少要的铁丝;若在框架四周和底部围上铁皮,至少需要的铁皮,围上铁皮后在里面最多能装水。
【点睛】本题考查长方体的总棱长、表面积和容积,熟记公式是解题的关键。
12. 4 96 64
【分析】根据正方体的特征,12条棱的长度都相等,根据正方体的棱长总和=棱长,用棱长总和除以12即可求出棱长,再根据正方体的表面积=棱长×棱长×6、正方体体积=棱长×棱长×棱长,列式计算即可。
【详解】棱长:分米
表面积:
平方分米
体积:立方分米
一个正方体的棱长总和是48分米,它的棱长是4分米,表面积是96平方分米,体积是64立方分米。
【点睛】此题考查的目的是理解掌握正方体的特征,以及正方体的表面积公式、体积公式的灵活运用。
13.21.5
【分析】观察可知,丝带长包括2条长、2条宽、4条高和结头,用长×2+宽×2+高×4+结头=丝带长度,据此列式计算。
【详解】
(厘米)
215厘米分米
要捆扎这种礼品盒,至少需要准备21.5分米的丝带。
【点睛】关键是掌握并灵活运用长方体棱长总和公式,注意统一单位。
14.(1) ①④ ②③
(2)4
【分析】(1)从正面看①是,②是,③是,④是,从上面看,①是,②是,③是,④是,据此填上相应序号。
(2)由6个完全相同的正方形围成的立体图形叫做正方体,如图,至少需要8个小正方体才能拼成一个大正方体,减去④中已有小正方体个数即可。
【详解】(1)从正面看,形状是的有①④;从上面看,形状是的有②③。
(2)8-4=4(个),如果要将④摆成一个较大的正方体,至少还需要4个相同的小正方体。
【点睛】关键是具有一定的空间想象能力,熟悉正方体的特征。
15.1.2立方米##1.2m3
【分析】长方体钢材沿横截面切成两段后,表面积增加了2个截面,增加的表面积÷2,求出一个截面面积,根据体积=截面面积×长,列式计算即可。
【详解】0.8÷2×3=1.2(立方米)
这段钢材原来的体积是1.2立方米。
【点睛】关键是掌握并灵活运用长方体体积公式。
16.√
【分析】从大正方体众拿掉小正方体,减少三个面的同时增加三个面,表面积不变。
【详解】由分析可知:
用8个大小相同的小正方体拼成一个大正方体,如果拿走其中一个小正方体,它的表面积不变。说法正确。
故答案为:√
【点睛】本题考查表面积,明确表面积的定义是解题的关键。
17.×
【分析】此题可设原来长、宽、高分别为a、b、c,那么现在就分别为2a、2b、2c,分别表示出原来与现在的棱长总和,即可得出答案。
【详解】解:设原来长为a,宽为b,高为c,则现在的长为2a,宽为2b,高为2c;
原来棱长总和:(a+a+c)×4=4(a+b+c)
现在棱长之和:(2a+2a+2c)×4=8(a+b+c)
棱长总和扩大:8(a+b+c)÷4(a+b+c)=2
一个长方体长、宽、高同时扩大到原来的2倍,那么它的棱长总和扩大到原来的2倍,原题说法错误。
故答案为:×
【点睛】此题主要考查长方体的棱长总和计算公式。
18.×
【分析】体积表示物体所占空间大小,表面积表示物体表面的总面积,两个概念不同,无法比较。
【详解】一个正方体的棱长总和是72厘米,它的体积和表面积无法比较,因为概念不同。
故答案为:×
【点睛】本题考查了体积和表面积的概念和区别。
19.√
【分析】根据正方体的表面积公式:S=6a2,所以表面积相等的两个正方体,则这两个正方体的棱长也相等,根据正方体的体积公式:V=a3,据此判断即可。
【详解】由分析可知:
表面积相等的两个正方体,它们的棱长也相等,所以它们的体积也相等。原题干说法正确。
故答案为:√
【点睛】本题考查正方体的表面积和体积,熟记公式是解题的关键。
20.√
【分析】根据正方体的特征可知,正方体的6个面都是相同的正方形;已知正方体的底面周长是8cm,即正方形的周长是8cm,根据正方形的边长=周长÷4,求出这个正方体的棱长;再根据正方体的体积=棱长×棱长×棱长,代入数据计算,据此判断。
【详解】8÷4=2(cm)
2×2×2
=4×2
=8(cm3)
底面周长是8cm的正方体,体积是8cm3。
原题说法正确。
故答案为:√
【点睛】本题考查正方体的特征、正方形的周长公式以及正方体体积公式的灵活应用,求出正方体的棱长是解题的关键。
21.(1)1000cm3;(2)120m3
【分析】正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,将数据代入公式,求出图形的体积即可。
【详解】(1)10×10×10=1000(cm3)
(2)4×2.5×12=120(m3)
22.表面积150;体积113
【分析】图形右上角缺口处露出了3个面,分别向外平移,正好补成一个棱长是5的大正方体,根据正方体的表面积=棱长×棱长×6,代入数据计算即可求出这个图形的表面积;
补好图形右上角的缺口,那么图形的体积=棱长为5的正方体的体积-长2、宽2、高3的长方体的体积;根据长方体的体积=长×宽×高,代入数据计算求出这个图形的体积。
【详解】如图:
表面积:
5×5×6
=25×6
=150
体积:
5×5×5-2×2×3
=125-12
=113
23.见详解
【分析】正方体一共有6个面,题中已经有5个面,只需要再补充1个面即可。补充完整后,通过想象将展开图折叠还原,观察能否还原成正方体,避免补充错误。
【详解】如图(答案不唯一):
【点睛】本题考查了正方体的展开图,有一定空间想象和图形认知能力是解题的关键。
24.1500立方厘米
【分析】从四角各剪去一个边长为5厘米的正方形,再做成无盖的长方体盒子,可得出这个长方体盒子的高为5厘米,底面长和宽分别是原来的长度减去10厘米得到,根据长方体体积=长×宽×高,据此可得出答案。
【详解】由题意可得:做成的无盖长方体盒子的长为(30−5−5)=20厘米,宽为(25−5−5)=15厘米,高为5厘米,则盒子的容积为:
(立方厘米)
答:这个盒子的容积是1500立方厘米。
【点睛】本题主要考查的是长方体的展开图及体积(容积)计算,解题的关键是熟练掌握长方体展开,进而计算得出答案。
25.1600平方厘米
【分析】正方体的六个面都是正方形,用棱长×棱长求出其中一个正方形的面积,再将其乘4,即可求出4个面的面积,即需要的商标纸的面积。
【详解】20×20×4=1600(平方厘米)
答:至少需要1600平方厘米的商标纸。
【点睛】本题考查了正方体的表面积,解题关键是明确求几个面的面积,避免犯错。
26.5厘米
【分析】观察图形可知,该长方体玻璃容器的长为20厘米,宽为5厘米,高为10厘米,用水的体积除以容器的底面积即可求出水面的高度。
【详解】500毫升=500立方厘米
500÷(20×5)
=500÷100
=5(厘米)
答:水面高5厘米。
【点睛】本题考查长方体的体积,熟记公式是解题的关键。
27.1936毫升
【分析】如下图所示,长方体纸盒的长是(30-4×2)厘米,宽是(30-4×2)厘米,高是剪去的正方形的边长4厘米。把盒子的长、宽、高代入长方体的体积计算公式(长方体的体积=长×宽×高),即可求出这个纸盒的容积。
【详解】
=484×4
(立方厘米)
1936立方厘米毫升
答:这个纸盒容积是1936毫升。
【点睛】用长方形纸板或正方形纸板制成盒子(四个角上分别去掉一个相同的小正方形),盒子的长和宽要在纸板的长和宽中去掉两个小正方形的边长,盒子的高是纸板四周去掉的小正方形的边长。
28.1立方分米
【分析】根据长方体的体积公式:长方体体积=长×宽×高,求出石头浸没水中后水和石头的体积和。最后,将其减去水的体积,求出石头的体积即可。
【详解】5升=5立方分米
2×2×1.5-5
=6-5
=1(立方分米)
答:石头的体积是1立方分米。
【点睛】此题考查了不规则物体体积的计算,找准数量关系,灵活运用长方体的体积公式。
29.36方;28800元
【分析】根据1平方米=100平方分米,统一单位,长方体体积=横截面的面积×长,据此求出一根方木的体积,乘方木数量,求出方木总体积,总体积×每立方米价格=要花的钱数,据此列式解答。
【详解】2.4平方分米=0.024平方米
0.024×3×500
=0.072×500
=36(方)
36×800=28800(元)
答:这批木料一共有36方(立方米),如果收购价是800元/方,这批木料要花28800元钱。
【点睛】关键是掌握并灵活运用长方体体积公式。
30.(1)7厘米
(2)245平方厘米
【分析】(1)由题意可知,因为两根铁丝的长度相同,所以长方体和正方体的总棱长也相等,根据长方体的总棱长公式:L=(a+b+h)×4,正方体的总棱长公式:L=12a,据此可求出正方体的棱长;
(2)由题意可知,彩纸的面积就是正方体五个面的面积,根据正方形的面积公式:S=a2,据此求出正方形的面积再乘5即可。
【详解】(1)(9+6+6)×4÷12
=21×4÷12
=84÷12
=7(厘米)
答:围成的正方体的棱长是7厘米。
(2)
(平方厘米)
答:在这个正方体的四周和底面贴上彩纸,需要245平方厘米的彩纸。
【点睛】本题考查长方体和正方体的总棱长及正方体的表面积,熟记公式是解题的关键。
31.会溢出,溢出24升
【分析】先根据正方体的体积=棱长×棱长×棱长,用4×4×4求出正方体铁块的体积,再根据长方体的体积=长×宽×高,用8×5×4求出长方体玻璃缸的体积,然后用正方体铁块的体积加上水的体积的和与长方体玻璃缸的体积比较,如果和大于长方体玻璃缸的体积,则会溢出,求出它们的差即可,如果和小于或等于长方体玻璃缸的体积,则不会溢出。
【详解】4×4×4
=16×4
=64(立方分米)
120升=120立方分米
64+120=184(立方分米)
8×5×4
=40×4
=160(立方分米)
184>160
184-160=24(立方分米)
24立方分米=24升
答:会溢出,溢出24升。
【点睛】本题考查了长方体体积公式和正方体体积公式的灵活应用。
相关试卷
这是一份人教版一年级下册3. 分类与整理当堂达标检测题,共18页。试卷主要包含了单一标准的分类,不同标准下的分类等内容,欢迎下载使用。
这是一份3.运算定律(拔高版)-2022-2023学年四年级下册数学期中专项复习(人教版),共16页。
这是一份3.长方体和正方体(培优版)-2022-2023学年五年级下册数学期中专项复习(人教版),共15页。










