2024年(新高考)高考数学一轮复习突破练习3.7《函数的图象》(含详解)

这是一份2024年(新高考)高考数学一轮复习突破练习3.7《函数的图象》(含详解)，共7页。试卷主要包含了7《函数的图象》，72－0等内容，欢迎下载使用。
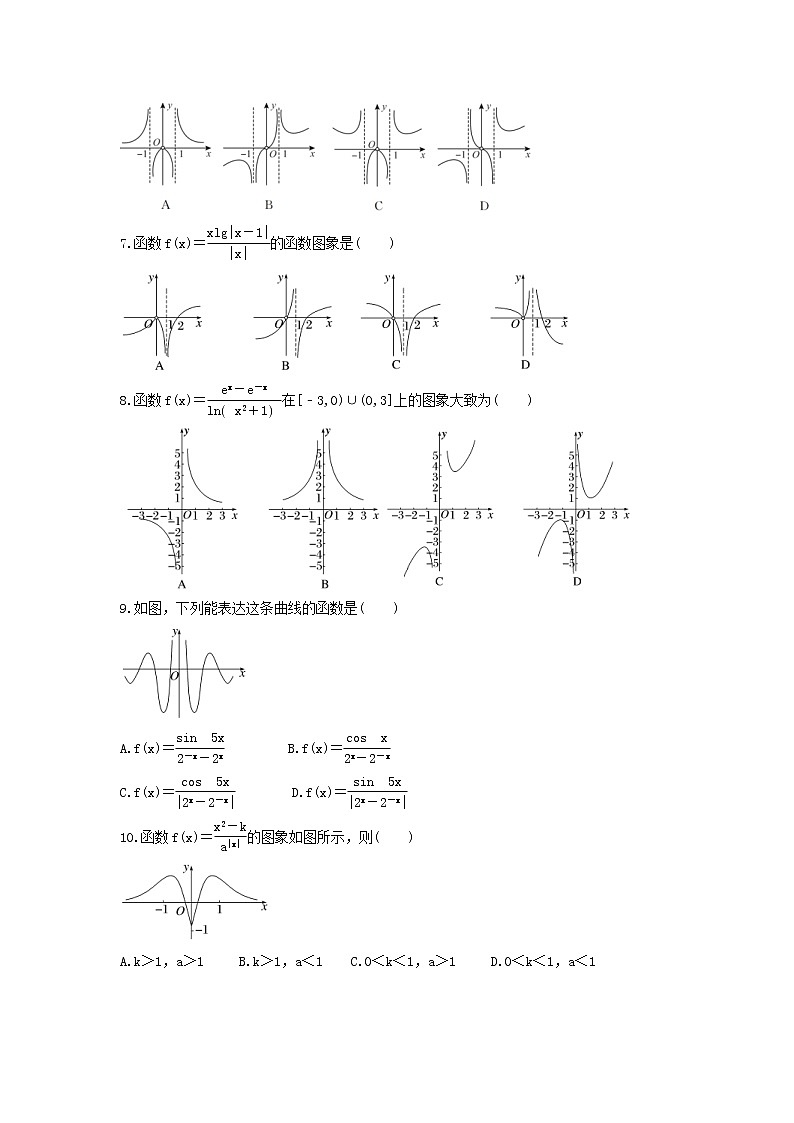
2024年(新高考)高考数学一轮复习突破练习3.7《函数的图象》一              、选择题1.下列函数中，其图象与函数y=lnx的图象关于直线x=1对称的是(　 　)A.y=ln(1－x)       B.y=ln(2－x)     C.y=ln(1＋x)       D.y=ln(2＋x)2.已知函数f(x)=x|x|－2x，则下列结论正确的是(　 　)A.f(x)是偶函数，递增区间是(0，＋∞)B.f(x)是偶函数，递减区间是(－∞，1)C.f(x)是奇函数，递减区间是(－1,1)D.f(x)是奇函数，递增区间是(－∞，0)3.函数y=－ex的图象(　 　)A.与y=ex的图象关于y轴对称B.与y=ex的图象关于坐标原点对称C.与y=e－x的图象关于y轴对称D.与y=e－x的图象关于坐标原点对称4.已知函数f(x)的图象如图所示，则f(x)的解析式可能是(　 　)A.f(x)=－x3   B.f(x)=＋x3    C.f(x)=－x3   D.f(x)=＋x35.现有四个函数：①y=xsinx；②y=xcosx；③y=x|cosx|；④y=x·2x.它们的图象(部分)如下，但顺序已被打乱，则按照从左到右将图象对应的函数序号排列正确的一组是(　 　)A.④①②③      B.①④③②     C.③④②①      D.①④②③6.函数f(x)=的图象大致是(　 　)7.函数f(x)＝的函数图象是(　　)   8.函数f(x)＝在[﹣3,0)∪(0,3]上的图象大致为(　　)9.如图，下列能表达这条曲线的函数是(　　)A.f(x)＝         B.f(x)＝C.f(x)＝        D.f(x)＝10.函数f(x)＝的图象如图所示，则(　　)A.k＞1，a＞1     B.k＞1，a＜1    C.0＜k＜1，a＞1     D.0＜k＜1，a＜111.已知函数f(x)＝，则函数y＝f(1﹣x)的大致图象是(　　)   12.已知函数f(x)=若a，b，c互不相等，且f(a)=f(b)=f(c)，则a＋b＋c的取值范围是(　 　)A.(1,2 017)      B.(1,2 018)       C.[2,2 018]      D.(2,2 018)二              、填空题13.设函数y=，关于该函数图像的命题如下：①一定存在两点，这两点的连线平行于x轴；②任意两点的连线都不平行于y轴；③关于直线y=x对称；④关于原点中心对称.其中正确的是________.14.偶函数y=f(x)的图像关于直线x=2对称，f(3)=3，则f(－1)=________.15.给定min{a，b}=已知函数f(x)=min{x，x2－4x＋4}＋4，若动直线y=m与函数y=f(x)的图象有3个交点，则实数m的取值范围为          .16.已知定义在R上的函数f(x)=关于x的方程f(x)=c(c为常数)恰有三个不同的实数根x1，x2，x3，则x1＋x2＋x3=       .
0.答案详解一              、选择题1.答案为：B.解析：解法1：设所求函数图象上任一点的坐标为(x，y)，则其关于直线x=1的对称点的坐标为(2－x，y)，由对称性知点(2－x，y)在函数f(x)=lnx的图象上，所以y=ln(2－x).故选B.解法2：由题意知，对称轴上的点(1,0)既在函数y=lnx的图象上也在所求函数的图象上，代入选项中的函数表达式逐一检验，排除A，C，D，故选B.2.答案为：C.解析：将函数f(x)=x|x|－2x去掉绝对值得f(x)=画出函数f(x)的图象，如图.观察图象可知，函数f(x)的图象关于原点对称，故函数f(x)为奇函数，且在(－1,1)上单调递减.3.答案为：D.解析：由点(x，y)关于原点的对称点是(－x，－y)，可知D正确.4.答案为：A；解析：由图可知，函数图象的渐近线为x=，排除C，D，又函数f(x)在，上单调递减.而函数y=在，上单调递减，y=－x3在R上单调递减，则f(x)=－x3在，上单调递减，故选A.5.答案为：D；解析：函数y=xsinx是偶函数，由图象知，函数①对应第一个图象；函数y=xcosx是奇函数，且当x=π时，y=－π＜0，故函数②对应第三个图象；函数y=x|cosx|为奇函数，且当x＞0时，y≥0，故函数③与第四个图象对应；函数y=x·2x为非奇非偶函数，与第二个图象对应.综上可知，选D.6.答案为：D；解析：由f(－x)=－f(x)可得f(x)是奇函数，图象关于原点对称，排除A，C，而x∈(0,1)时，ln|x|＜0，f(x)＜0，排除B，故选D.7.答案为：A.解析：去绝对值可得f(x)＝＝当x＞1时，y＝lg(x﹣1)单调递增，当0＜x＜1时，y＝lg单调递减，且y＜0，当x＜0时，y＝﹣lg单调递增，且y＜0，综上，只有A符合.8.答案为：C.解析：函数f(x)＝，x∈[﹣3,0)∪(0,3]，则f(﹣x)＝＝﹣f(x)，所以f(x)在定义域上为奇函数，排除B选项；当x→＋∞时，f(x)＝→＋∞，排除A选项；当x＝1时，f(1)＝＝≈≈3.4，排除D选项；综上可知，C为正确选项.9.答案为：C解析：观察图象可知，函数的图象关于y轴对称，应是偶函数，选项B，f(﹣x)＝＝＝﹣f(x)，是奇函数，图象关于原点对称，不符合题意，选项D，f(﹣x)＝＝﹣＝﹣f(x)，是奇函数，图象关于原点对称，不符合题意，选项A，当x∈时，f(x)＜0，不符合题意.10.答案为：C解析：因为f(0)＝﹣k，据图象知﹣1＜﹣k＜0，所以0＜k＜1，排除A，B，又由x→＋∞时，f(x)→0，从而a＞1.11.答案为：D.解析：先画出函数f(x)＝的大致图象，令函数f(x)的图象关于y轴对称，得函数f(﹣x)的图象，再把所得的函数f(﹣x)的图象，向右平移1个单位长度，得到函数y＝f(1﹣x)的图象.12.答案为：D；解析：设f(a)=f(b)=f(c)=m，作出函数f(x)的图象与直线y=m，如图所示，不妨设a＜b＜c，当0≤x≤1时，函数f(x)的图象与直线y=m的交点分别为A，B，由正弦曲线的对称性，可得A(a，m)与B(b，m)关于直线x=对称，因此a＋b=1，令log2 017x=1，解得x=2 017，结合图象可得1＜c＜2 017，因此可得2＜a＋b＋c＜2 018，即a＋b＋c∈(2,2 018).故选D.二              、填空题13.答案为：②③.解析：[y===2＋，图像如图所示，可知②③正确.]14.答案为：3.解析：[由题意知f(－1)=f(1)=f(3)=3.]15.答案为：(4,5).解析：作出函数f(x)的图象，函数f(x)=min{x，x2－4x＋4}＋4的图象如图所示，由于直线y=m与函数y=f(x)的图象有3个交点，数形结合可得m的取值范围为(4,5).16.答案为：0.解析：方程f(x)=c有三个不同的实数根等价于y=f(x)与y=c的图象有三个交点，画出函数f(x)的图象(图略)，易知c=1，且方程f(x)=c的一根为0，令lg|x|=1，解得x=－10或10，故方程f(x)=c的另两根为－10和10，所以x1＋x2＋x3=0.