2023年辽宁省沈阳市大东区中考数学零模试卷

这是一份2023年辽宁省沈阳市大东区中考数学零模试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年辽宁省沈阳市大东区中考数学零模试卷
一、选择题（下列各题的备选答案中，只有一个答案是正确的.每小题2分，共20分）
1．（2分）下列计算结果为5的是（　　）
A．﹣（+5） B．+（﹣5） C．﹣（﹣5） D．﹣|﹣5|
2．（2分）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
3．（2分）如图①，用一个平面截长方体，得到如图②的几何体，它在我国古代数学名著《九章算术》中被称为“堑堵”．图②“堑堵”的俯视图是（　　）

A． B．
C． D．
4．（2分）2022年3月11日，新华社发文总结2021年中国取得的科技成就，其中包括“奋斗者”号载人潜水器最深下潜至10909米．其中数据10909用科学记数法表示为（　　）
A．10.909×102 B．1.0909×103
C．0.10909×104 D．1.0909×104
5．（2分）下列计算结果正确的是（　　）
A．5a﹣3a＝2 B．6a÷2a＝3a
C．a6÷a3＝a2 D．（2a2b3）3＝8a6b9
6．（2分）在一个不透明的布袋内，有红球5个，黄球4个，白球1个，蓝球3个，它们除颜色外，大小、质地都相同．若随机从袋中摸取一个球，则摸中哪种球的概率最大（　　）
A．红球 B．黄球 C．白球 D．蓝球
7．（2分）一个多边形的内角和为900°，则这个多边形是（　　）
A．七边形 B．八边形 C．九边形 D．十边形
8．（2分）已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b的值为（　　）
A．6 B．5 C．4 D．3
9．（2分）如图，OA，OB是⊙O的两条半径，点C在⊙O上，若∠AOB＝80°，则∠C的度数为（　　）

A．30° B．40° C．50° D．60°
10．（2分）满足不等式组的整数解是（　　）
A．4 B．3 C．2 D．1
二、填空题（每小题3分，共18分）
11．（3分）因式分解：x2﹣x4＝　 　．
12．（3分）在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同，方差分别为S甲2＝1.50，S乙2＝0.75，则考核成绩更为稳定的运动员是 　 　（填“甲”、“乙”中的一个）．
13．（3分）若一元二次方程x2+2x+k＝0有两个相等的实数根，则k的值为 　 　．
14．（3分）如图，直线AB交x轴于点C，交反比例函数y＝（a＞0）的图象于A，B两点，过点B作BD⊥y轴，垂足为点D，连接CD，若S△BCD＝5，则a的值为 　 　．

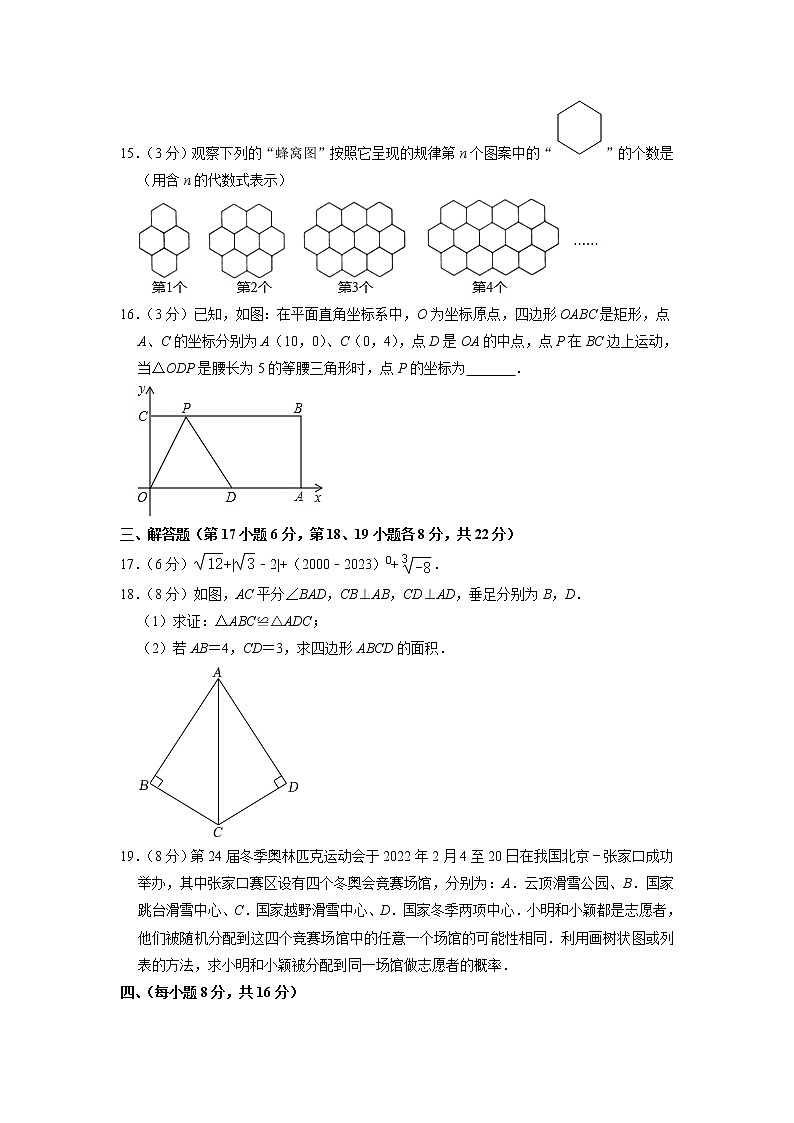
15．（3分）观察下列的“蜂窝图”按照它呈现的规律第n个图案中的“”的个数是　 　（用含n的代数式表示）

16．（3分）已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为　 　．

三、解答题（第17小题6分，第18、19小题各8分，共22分）
17．（6分）+|﹣2|+（2000﹣2023）0+．
18．（8分）如图，AC平分∠BAD，CB⊥AB，CD⊥AD，垂足分别为B，D．
（1）求证：△ABC≌△ADC；
（2）若AB＝4，CD＝3，求四边形ABCD的面积．

19．（8分）第24届冬季奥林匹克运动会于2022年2月4至20日在我国北京﹣张家口成功举办，其中张家口赛区设有四个冬奥会竞赛场馆，分别为：A．云顶滑雪公园、B．国家跳台滑雪中心、C．国家越野滑雪中心、D．国家冬季两项中心．小明和小颖都是志愿者，他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同．利用画树状图或列表的方法，求小明和小颖被分配到同一场馆做志愿者的概率．
四、（每小题8分，共16分）
20．（8分）在中国共产主义青年团成立100周年时，某校组织学生观看庆祝大会实况并进行团史学习．现随机抽取部分学生进行团史知识竞赛，并将竞赛成绩进行整理（成绩得分用a表示），其中60≤α＜70记为“较差”，70≤α＜80记为“一般”，80≤α＜90记为“良好”，90≤α≤100记为“优秀”，绘制了如图不完整的扇形统计图和频数分布直方图．

根据统计图提供的信息，回答如下问题：
（1）被随机抽取的学生总人数是 　 　；
（2）直接将直方图补充完整；
（3）“一般”对应的百分比x＝　 　，“优秀”对应的百分比y＝　 　；
（4）已知90≤α≤100这组的具体成绩为93，94，99，91，100，94，96，98，则这8个数据的中位数是 　 　，众数是 　 　；
（5）若该校共有1000人，估计该校学生对团史掌握程度达到“优秀”的人数．
21．（8分）为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质，某校定期开展劳动实践活动．甲、乙两班在一次体验摘草莓的活动中，甲班摘120千克草莓与乙班摘150千克草莓所用的时间相同．已知甲班平均每小时比乙班少摘10千克草莓，问乙班平均每小时摘多少千克草莓？
五、（本题10分）
22．（10分）如图，△ABC中，AB＝AC，D为AC上一点，以CD为直径的半⊙O与AB相切于点E，交BC于点F，FG⊥AB，垂足为G．
（1）求证：FG是⊙O的切线；
（2）若BG＝2，BF＝6，直接写出CF的长．

六、（本题10分）
23．（10分）如图，△ABC在平面直角坐标系中，点A在x的负半轴上，点B在x的正半轴上，点C在y的正半轴上，∠ACB＝90°，∠A＝30°，AB＝6，动点P从点A出发，以2个单位长度/s的速度沿边AB向终点B匀速运动，以PA为一边作∠APG＝120°，另一边PG与折线AC﹣CB相交于点G，以PG为边作菱形PGFE，点E在线段PB上．设点P的运动时间为x（s）．
（1）当点G在边AC上，直接写出PG的长为 　 　（用含x的代数式表示）；
（2）当点F落在边BC上时，
①求x的值；
②直接写出此时点E，点F的坐标；
③点M在y轴上，点Q在直线BC上，当以E，F，M，Q四个点为顶点的四边形是平行四边形时，直接写出点Q的坐标．

七、（本题12分）
24．（12分）已知CD是△ABC中∠C的角平分线，点E，F分别在边AC，BC上，AD＝m，BD＝n．△ADE与△BDF的面积之和为S．
（1）当∠ACB＝90°，DE⊥AC，DF⊥BC时，如图1，若∠B＝45°，m＝3，则n＝　 　，S＝　 　；
（2）如图2，当∠ACB＝∠EDF＝90°时，
①求证：DE＝DF；
②直接写出S与m，n的数量关系；
（3）如图3，当∠ACB＝60°，∠EDF＝120°，m＝6，n＝4时，请直接写出S的大小．

八、（本题12分）
25．（12分）已知抛物线y＝﹣x2+4x+c与x轴交于A，B两点，点A在点B的左侧，与y轴交于点C（0，5）．
（1）直接写出A点坐标（ 　 　，　 　），B点坐标（ 　 　，　 　）；
（2）求抛物线顶点M的坐标；
（3）如图1，点D是抛物线上位于对称轴右侧的一个动点，且点D在第一象限内，过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，垂足为点F，当四边形DEFG的周长最大时，求点D的坐标；
（4）如图2，将△MBC沿BC翻折得到△NBC，NB与y轴交于点Q，在对称轴上找一点P，使得△PQB是直角三角形，直接写出所有符合条件的点P的坐标．


2023年辽宁省沈阳市大东区中考数学零模试卷
（参考答案与详解）
一、选择题（下列各题的备选答案中，只有一个答案是正确的.每小题2分，共20分）
1．（2分）下列计算结果为5的是（　　）
A．﹣（+5） B．+（﹣5） C．﹣（﹣5） D．﹣|﹣5|
【解答】解：A选项，原式＝﹣5，故该选项不符合题意；
B选项，原式＝﹣5，故该选项不符合题意；
C选项，原式＝5，故该选项符合题意；
D选项，原式＝﹣5，故该选项不符合题意；
故选：C．
2．（2分）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【解答】解：A．该图形既不是中心对称图形，也不是轴对称图形，故此选项不合题意；
B．该图形是轴对称图形，不是中心对称图形，故此选项不合题意；
C．该图形既不是中心对称图形，也不是轴对称图形，故此选项不合题意；
D．该图形既是轴对称图形又是中心对称图形，故此选项符合题意．
故选：D．
3．（2分）如图①，用一个平面截长方体，得到如图②的几何体，它在我国古代数学名著《九章算术》中被称为“堑堵”．图②“堑堵”的俯视图是（　　）

A． B．
C． D．
【解答】解：图②“堑堵”从上面看，是一个矩形，
故选：C．
4．（2分）2022年3月11日，新华社发文总结2021年中国取得的科技成就，其中包括“奋斗者”号载人潜水器最深下潜至10909米．其中数据10909用科学记数法表示为（　　）
A．10.909×102 B．1.0909×103
C．0.10909×104 D．1.0909×104
【解答】解：10909＝1.0909×104，
故选：D．
5．（2分）下列计算结果正确的是（　　）
A．5a﹣3a＝2 B．6a÷2a＝3a
C．a6÷a3＝a2 D．（2a2b3）3＝8a6b9
【解答】解：A选项，原式＝2a，故该选项不符合题意；
B选项，原式＝3，故该选项不符合题意；
C选项，原式＝a3，故该选项不符合题意；
D选项，原式＝8a6b9，故该选项符合题意；
故选：D．
6．（2分）在一个不透明的布袋内，有红球5个，黄球4个，白球1个，蓝球3个，它们除颜色外，大小、质地都相同．若随机从袋中摸取一个球，则摸中哪种球的概率最大（　　）
A．红球 B．黄球 C．白球 D．蓝球
【解答】解：在一个不透明的布袋内，有红球5个，黄球4个，白球1个，蓝球3个，它们除颜色外，大小、质地都相同．若随机从袋中摸取一个球，
因为红球的个数最多，所以摸到红球的概率最大，
摸到红球的概率是：，
故选：A．
7．（2分）一个多边形的内角和为900°，则这个多边形是（　　）
A．七边形 B．八边形 C．九边形 D．十边形
【解答】解：设多边形的边数为n，
（n﹣2）•180°＝900°，
解得：n＝7．
故选：A．
8．（2分）已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b的值为（　　）
A．6 B．5 C．4 D．3
【解答】解：∵点A（﹣2，b）与点B（a，3）关于原点对称，
∴a＝2，b＝﹣3，
∴a﹣b＝2+3＝5，
故选：B．
9．（2分）如图，OA，OB是⊙O的两条半径，点C在⊙O上，若∠AOB＝80°，则∠C的度数为（　　）

A．30° B．40° C．50° D．60°
【解答】解：∵OA，OB是⊙O的两条半径，点C在⊙O上，∠AOB＝80°，
∴∠C＝＝40°．
故选：B．
10．（2分）满足不等式组的整数解是（　　）
A．4 B．3 C．2 D．1
【解答】解：由2x﹣5≤0得：x≤，
由x﹣1＞0得：x＞1，
则不等式组的解集为1＜x≤，
∴不等式组的整数解为2，
故选：C．
二、填空题（每小题3分，共18分）
11．（3分）因式分解：x2﹣x4＝　x2（1+x）（1﹣x）　．
【解答】解：原式＝x2（1﹣x2）
＝x2（1+x）（1﹣x）．
故答案为：x2（1+x）（1﹣x）．
12．（3分）在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同，方差分别为S甲2＝1.50，S乙2＝0.75，则考核成绩更为稳定的运动员是 　乙　（填“甲”、“乙”中的一个）．
【解答】解：∵两人的考核成绩的平均数相同，方差分别为S甲2＝1.50，S乙2＝0.75，
∴S甲2＞S乙2，
∴考核成绩更为稳定的运动员是乙；
故答案为：乙．
13．（3分）若一元二次方程x2+2x+k＝0有两个相等的实数根，则k的值为 　1　．
【解答】解：根据题意得Δ＝22﹣4×1×k＝0，即4﹣4k＝0
解得k＝1．
故答案为：1．
14．（3分）如图，直线AB交x轴于点C，交反比例函数y＝（a＞0）的图象于A，B两点，过点B作BD⊥y轴，垂足为点D，连接CD，若S△BCD＝5，则a的值为 　10　．

【解答】解：连接OB，
∵BD⊥y轴，
∴S△BOD＝|a|，
∵BD∥x轴，
∴S△BCD＝S△BOD＝|a|，
∵S△BCD＝5，
∴＝5，
∵a＞0，
解得：a＝10，
故答案为：10．

15．（3分）观察下列的“蜂窝图”按照它呈现的规律第n个图案中的“”的个数是　3n+1　（用含n的代数式表示）

【解答】解：由题意可知：每1个都比前一个多出了3个“”，
∴第n个图案中共有“”为：4+3（n﹣1）＝3n+1
故答案为：3n+1
16．（3分）已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为　（3，4）或（2，4）或（8，4）　．

【解答】解：（1）OD是等腰三角形的底边时，P就是OD的垂直平分线与CB的交点，此时OP＝PD≠5；
（2）OD是等腰三角形的一条腰时：
①若点O是顶角顶点时，P点就是以点O为圆心，以5为半径的弧与CB的交点，
在直角△OPC中，CP＝＝＝3，则P的坐标是（3，4）．
②若D是顶角顶点时，P点就是以点D为圆心，以5为半径的弧与CB的交点，
过D作DM⊥BC于点M，
在直角△PDM中，PM＝＝3，
当P在M的左边时，CP＝5﹣3＝2，则P的坐标是（2，4）；
当P在M的右侧时，CP＝5+3＝8，则P的坐标是（8，4）．
故P的坐标为：（3，4）或（2，4）或（8，4）．
故答案为：（3，4）或（2，4）或（8，4）．

三、解答题（第17小题6分，第18、19小题各8分，共22分）
17．（6分）+|﹣2|+（2000﹣2023）0+．
【解答】解：+|﹣2|+（2000﹣2023）0+
＝2+2﹣+1+（﹣2）
＝+1．
18．（8分）如图，AC平分∠BAD，CB⊥AB，CD⊥AD，垂足分别为B，D．
（1）求证：△ABC≌△ADC；
（2）若AB＝4，CD＝3，求四边形ABCD的面积．

【解答】（1）证明：∵AC平分∠BAD，
∴∠BAC＝∠DAC，
∵CB⊥AB，CD⊥AD，
∴∠B＝90°＝∠D，
在△ABC和△ADC中，
，
∴△ABC≌△ADC（AAS）；
（2）解：由（1）知：△ABC≌△ADC，
∴BC＝CD＝3，S△ABC＝S△ADC，
∴S△ABC＝AB•BC＝×4×3＝6，
∴S△ADC＝6，
∴S四边形ABCD＝S△ABC+S△ADC＝12，
答：四边形ABCD的面积是12．
19．（8分）第24届冬季奥林匹克运动会于2022年2月4至20日在我国北京﹣张家口成功举办，其中张家口赛区设有四个冬奥会竞赛场馆，分别为：A．云顶滑雪公园、B．国家跳台滑雪中心、C．国家越野滑雪中心、D．国家冬季两项中心．小明和小颖都是志愿者，他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同．利用画树状图或列表的方法，求小明和小颖被分配到同一场馆做志愿者的概率．
【解答】解：画树状图如下：

共有16种等可能的结果，其中小明和小颖被分配到同一场馆做志愿者的结果有4种，
∴小明和小颖被分配到同一场馆做志愿者的概率为＝．
四、（每小题8分，共16分）
20．（8分）在中国共产主义青年团成立100周年时，某校组织学生观看庆祝大会实况并进行团史学习．现随机抽取部分学生进行团史知识竞赛，并将竞赛成绩进行整理（成绩得分用a表示），其中60≤α＜70记为“较差”，70≤α＜80记为“一般”，80≤α＜90记为“良好”，90≤α≤100记为“优秀”，绘制了如图不完整的扇形统计图和频数分布直方图．

根据统计图提供的信息，回答如下问题：
（1）被随机抽取的学生总人数是 　50　；
（2）直接将直方图补充完整；
（3）“一般”对应的百分比x＝　30%　，“优秀”对应的百分比y＝　16%　；
（4）已知90≤α≤100这组的具体成绩为93，94，99，91，100，94，96，98，则这8个数据的中位数是 　95　，众数是 　94　；
（5）若该校共有1000人，估计该校学生对团史掌握程度达到“优秀”的人数．
【解答】解：（1）被随机抽取的学生总人数是：4÷8%＝50，
故答案为：50；
（2）2组的人数为50﹣4﹣23﹣8＝15，
将直方图补充完整如下：

（3）“一般”对应的百分比x＝；
“优秀”对应的百分比y＝＝16%；
故答案为：30%；16%
（4）“90≤α≤100”这组的数据重新排列如下：91，93，94，94，96，98，99，100，
∴90≤α≤100”这组数据的众数是94，中位数是＝95．
故答案为：95，94；
（5）1000×16%＝160（人），
答：估计该校学生对团史掌握程度达到“优秀”的人数大约为160人．
21．（8分）为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质，某校定期开展劳动实践活动．甲、乙两班在一次体验摘草莓的活动中，甲班摘120千克草莓与乙班摘150千克草莓所用的时间相同．已知甲班平均每小时比乙班少摘10千克草莓，问乙班平均每小时摘多少千克草莓？
【解答】解：设乙班平均每小时摘x千克草莓，则甲班平均每小时摘（x﹣10）千克草莓，
根据题意得：＝，
解得：x＝50，
经检验，x＝50是所列方程的解，且符合题意．
答：乙班平均每小时摘50千克草莓．
五、（本题10分）
22．（10分）如图，△ABC中，AB＝AC，D为AC上一点，以CD为直径的半⊙O与AB相切于点E，交BC于点F，FG⊥AB，垂足为G．
（1）求证：FG是⊙O的切线；
（2）若BG＝2，BF＝6，直接写出CF的长．

【解答】（1）证明：连接OF，
∵AB＝AC，
∴∠B＝∠C，
∵OF＝OC，
∴∠C＝∠OFC，
∴∠OFC＝∠B，
∴OF∥AB，
∵AB⊥FG，
∴半径OF⊥FG，
∴FG是⊙O的切线；
（2）解：连接OE，FD，
∵AB与圆相切于E，
∴∠OEG＝90°，
∵∠EGF＝∠OFG＝90°，
∴四边形EGFO是矩形，
∴FG＝OE，
∵FG＝＝＝4，
∴CD＝2OE＝8，
∵CD是半圆的直径，
∴∠DFC＝90°，
∵∠B＝∠C，∠BGF＝∠DFC＝90°，
∴∠CDF＝∠BFG，
∴sin∠CDF＝sin∠BFG，
∴＝，
∴＝，
∴CF＝．

六、（本题10分）
23．（10分）如图，△ABC在平面直角坐标系中，点A在x的负半轴上，点B在x的正半轴上，点C在y的正半轴上，∠ACB＝90°，∠A＝30°，AB＝6，动点P从点A出发，以2个单位长度/s的速度沿边AB向终点B匀速运动，以PA为一边作∠APG＝120°，另一边PG与折线AC﹣CB相交于点G，以PG为边作菱形PGFE，点E在线段PB上．设点P的运动时间为x（s）．
（1）当点G在边AC上，直接写出PG的长为 　2x（0＜x≤）　（用含x的代数式表示）；
（2）当点F落在边BC上时，
①求x的值；
②直接写出此时点E，点F的坐标；
③点M在y轴上，点Q在直线BC上，当以E，F，M，Q四个点为顶点的四边形是平行四边形时，直接写出点Q的坐标．

【解答】解：（1）∵∠APG＝120°，∠A＝30°，
∴∠AGP＝180°﹣120°﹣30°＝30°，
∴PG＝PA＝2x（0＜x≤）．
故答案为：2x（0＜x≤）；
（2）①

∵∠APG＝120°，
∴∠GPF＝180°﹣120°＝60°，
∵四边形PGFE是菱形，
∴PG＝EF＝PE＝GF＝2x，EF∥PG，
∴∠FEB＝∠GPE＝60°，
∵∠ACB＝90°，∠CAB＝30°，
∴∠ABC＝60°，
∴△BEF是等边三角形，
∴EF＝BE＝2x，
∵AP+PE+EB＝6，
∴6x＝6，
∴x＝1；
②在Rt△ACB中，∠ACB＝90°，AB＝6，∠CAB＝30°，
∴BC＝AB＝3，∠ABC＝60°，
∵∠COB＝90°，∠OCB＝30°，
∴OB＝BC＝，
∵EB＝2，
∴OE＝BE﹣OB＝2﹣＝，
∴E（﹣，0），
过点F作FH⊥BE于点H．
∵△EFB是等边三角形，
∴EH＝BH＝BF＝1，FH＝BH＝，
∴OH＝OB﹣BH＝，
∴F（，）；
③当点M在x轴的下方时，点Q在线段BF上是由点F向右平移个单位得到，可得Q（1，）．

当点M′在x轴的上方时，Q′与Q关于点C对称，此时Q′（﹣1，）．
综上所述，满足条件点Q的坐标为（1，）或（﹣1，）．
七、（本题12分）
24．（12分）已知CD是△ABC中∠C的角平分线，点E，F分别在边AC，BC上，AD＝m，BD＝n．△ADE与△BDF的面积之和为S．
（1）当∠ACB＝90°，DE⊥AC，DF⊥BC时，如图1，若∠B＝45°，m＝3，则n＝　3　，S＝　9　；
（2）如图2，当∠ACB＝∠EDF＝90°时，
①求证：DE＝DF；
②直接写出S与m，n的数量关系；
（3）如图3，当∠ACB＝60°，∠EDF＝120°，m＝6，n＝4时，请直接写出S的大小．

【解答】（1）解：如图1中，∵∠ACB＝90°，∠B＝45°，
∴CA＝CB，
∵CD平分∠ACB，
∴AD＝DB＝3，
∵DE⊥AC，DF⊥BC，∠A＝∠B＝45°，
∴△ADE，△BDF都是等腰直角三角形，
∴BF＝DF＝3，AE＝DE＝3，
∴S＝×3×3+×3×3＝9，
故答案为：3，9；

（2）①证明：如图2中，过点D作DM⊥AC于点M，DN⊥BC于点N．

∵DM⊥AC，DN⊥BC，CD平分∠ACB，
∴DM＝DN，
∵∠DMC＝∠DNC＝∠MCN＝90°，
∴四边形DNCM是矩形，
∴DM＝DN，
∴四边形DMCN是正方形，
∴∠MDN＝∠EDF＝90°，
∴∠MDE＝∠NDF，
∵∠DME＝∠DNF，
∴△DME≌△DNF（ASA），
∴DE＝DF；

②解：∵△DME≌△DNF，
∴S△DME＝S△DNF，
∴S＝S△ADE+S△BDF＝S△ADM+S△BDN，
把△BDN绕点D逆时针旋转90°得到右边△ADH，∠ADH＝90°，AD＝m，DH＝n，
∴S＝mn；

（3）如图3中，过点D作DM⊥AC于点M，DN⊥BC于点N．

∵DM⊥AC，DN⊥BC，CD平分∠ACB，
∴DM＝DN，
∵∠DMC＝∠DNC＝90°，
∴∠MDN＝180°﹣∠ACB＝120°，
∴∠EDF＝∠MDN＝120°，
∴∠EDM＝∠FDN，
∵∠DME＝∠DNF＝90°，
∴△DME≌△DNF（AAS），
∴S△DME＝S△DNF，
∴S＝S△ADE+S△BDF＝S△ADM+S△BDN，
把△ADM绕点D顺时针旋转120°得到△DNT，∠BDT＝60°，DT＝6，DB＝4，
过点B作BH⊥DT于点H，
∴BH＝BD×sin60°＝4×＝2，
∴S＝S△BDT＝×6×2＝6．
八、（本题12分）
25．（12分）已知抛物线y＝﹣x2+4x+c与x轴交于A，B两点，点A在点B的左侧，与y轴交于点C（0，5）．
（1）直接写出A点坐标（ 　﹣1　，　0　），B点坐标（ 　5　，　0　）；
（2）求抛物线顶点M的坐标；
（3）如图1，点D是抛物线上位于对称轴右侧的一个动点，且点D在第一象限内，过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，垂足为点F，当四边形DEFG的周长最大时，求点D的坐标；
（4）如图2，将△MBC沿BC翻折得到△NBC，NB与y轴交于点Q，在对称轴上找一点P，使得△PQB是直角三角形，直接写出所有符合条件的点P的坐标．

【解答】解：（1）∵抛物线与y轴交于点C（0，5）．
∴c＝5，
∴这个抛物线的解析式为：y＝﹣x2+4x+5，
令y＝0，则﹣x2+4x+5＝0，解得x1＝5，x2＝﹣1，
∴点A（﹣1，0）、B（5，0），
故答案为：﹣1，0；5，0；

（2）∵抛物线的解析式为：y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴M的坐标为：（2，9）；

（3）由（2）知，抛物线的对称轴为x＝2，
设D（x，﹣x2+4x+5），
∵DE∥x轴，
∴E（4﹣x，﹣x2+4x+5），

∵过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，
∴四边形DEFG是矩形，
∴四边形DEFG的周长＝2（﹣x2+4x+5）+2（x﹣4+x）＝﹣2x2+12x+2＝﹣2（x﹣3）2+20，
∴当x＝3时，四边形DEFG的周长最大，
∴当四边形DEFG的周长最大时，点D的坐标为（3，8）；

（4）过点C作CH⊥对称轴于H，过点N作NK⊥y轴于K，

由翻折得CN＝CM，∠BCN＝∠BCM，
∵B（5，0），C（0，5）．
∴OB＝OC，
∴∠OCB＝∠OBC＝45°，
∵CH⊥对称轴于H，
∴CH∥x轴，
∴∠BCH＝45°，
∴∠BCH＝∠OCB，
∴∠NCK＝∠MCH，
∴△MCH≌△NCK（AAS），
∴NK＝MH，CK＝CH，
∵抛物线的解析式为：y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴对称轴为x＝2，M（2，9），
∴MH＝9﹣5＝4，CH＝2，
∴NK＝MH＝4，CK＝CH＝2，
∴N（﹣4，3），
设直线BN的解析式为y＝mx+n，
∴，解得：，
∴直线BN的解析式为y＝﹣x+，
∴Q（0，），
设P（2，p），
∴PQ2＝22+（p﹣）2＝p2﹣p+，
BP2＝（5﹣2）2+p2＝9+p2，
BQ2＝52+（）2＝25+，
分三种情况：
①当∠BQP＝90°时，BP2＝PQ2+BQ2，
∴9+p2＝p2﹣p++25+，解得p＝，
∴点P的坐标为（2，）；
②当∠QBP＝90°时，P′Q2＝BP′2+BQ2，
∴p2﹣p+＝9+p2+25+，解得p＝﹣9，
∴点P′的坐标为（2，﹣9）．
③当∠BPQ＝90°时，
25+＝p2﹣p++9+p2，
解得：p＝，
即点P的坐标为：（2，）或（2，）；
综上，所有符合条件的点P的坐标为（2，），（2，﹣9）或（2，）或（2，）．