2023年黑龙江省虎林市实验中学中考一模数学试题

二〇二三年初中生学业水平考试

数学试题

考生注意：

1.考试时间120分钟

2.全卷共三道大题，总分120分

一、选择题（每题3分，满分30分）

1.下列运算正确的是（    ）

A.    B.

C.   D.

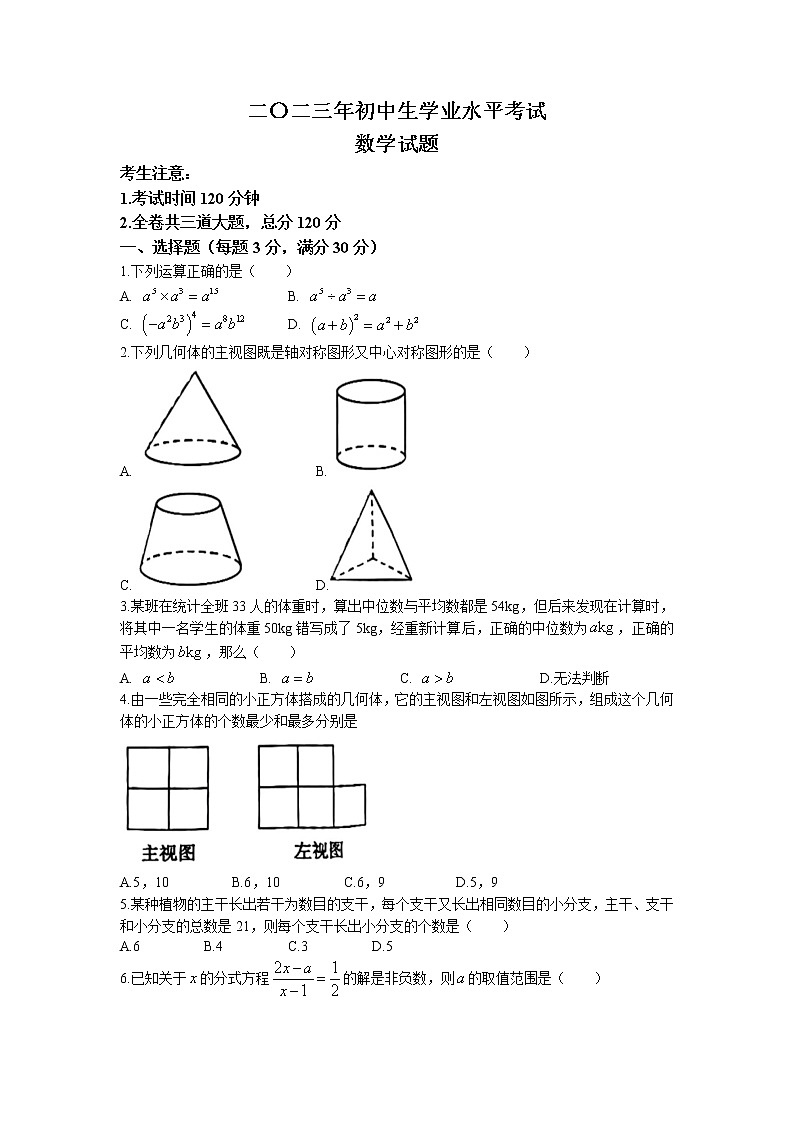
2.下列几何体的主视图既是轴对称图形又中心对称图形的是（    ）

A.   B.

C.   D.

3.某班在统计全班33人的体重时，算出中位数与平均数都是54kg，但后来发现在计算时，将其中一名学生的体重50kg错写成了5kg，经重新计算后，正确的中位数为，正确的平均数为，那么（    ）

A.    B.    C.    D.无法判断

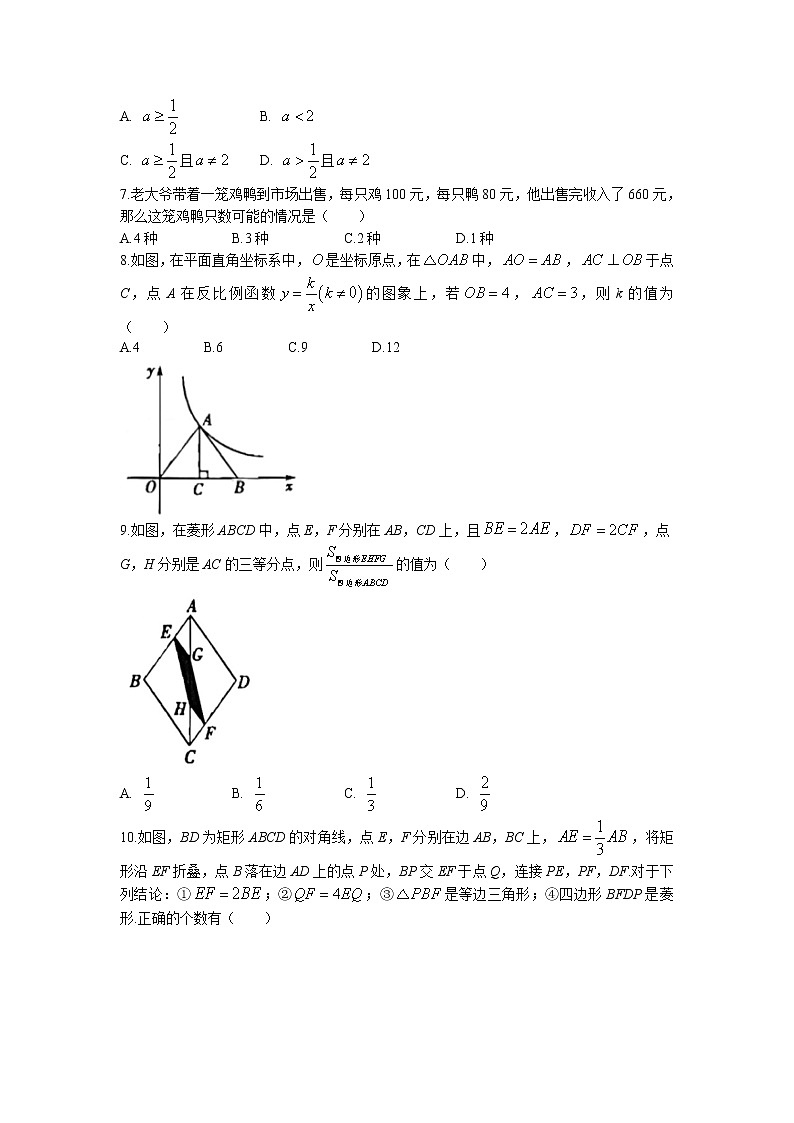
4.由一些完全相同的小正方体搭成的几何体，它的主视图和左视图如图所示，组成这个几何体的小正方体的个数最少和最多分别是

A.5，10   B.6，10   C.6，9   D.5，9

5.某种植物的主干长出若干为数目的支干，每个支干又长出相同数目的小分支，主干、支干和小分支的总数是21，则每个支干长出小分支的个数是（    ）

A.6   B.4   C.3   D.5

6.已知关于的分式方程的解是非负数，则的取值范围是（    ）

A.    B.

C. 且  D. 且

7.老大爷带着一笼鸡鸭到市场出售，每只鸡100元，每只鸭80元，他出售完收入了660元，那么这笼鸡鸭只数可能的情况是（    ）

A.4种   B.3种   C.2种   D.1种

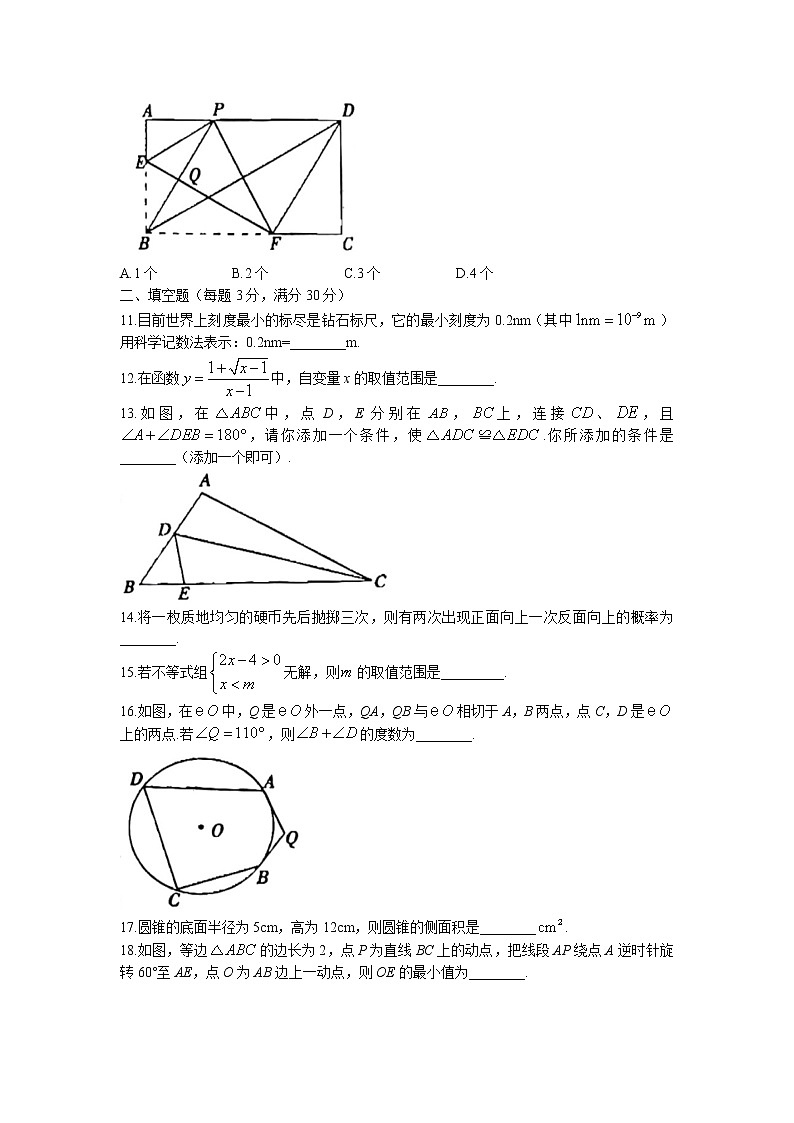
8.如图，在平面直角坐标系中，是坐标原点，在中，，于点C，点A在反比例函数的图象上，若，，则k的值为（    ）

A.4   B.6   C.9   D.12

9.如图，在菱形ABCD中，点E，F分别在AB，CD上，且，，点G，H分别是AC的三等分点，则的值为（    ）

A.    B.    C.    D.

10.如图，BD为矩形ABCD的对角线，点E，F分别在边AB，BC上，，将矩形沿EF折叠，点B落在边AD上的点Р处，BP交EF于点Q，连接PE，PF，DF.对于下列结论：①；②；③是等边三角形；④四边形BFDP是菱形.正确的个数有（    ）

A.1个   B.2个   C.3个   D.4个

二、填空题（每题3分，满分30分）

11.目前世界上刻度最小的标尽是钻石标尺，它的最小刻度为0.2nm（其中）用科学记数法表示：0.2nm=________m.

12.在函数中，自变量x的取值范围是________.

13.如图，在中，点D，E分别在，上，连接、，且，请你添加一个条件，使.你所添加的条件是________（添加一个即可）.

14.将一枚质地均匀的硬币先后抛掷三次，则有两次出现正面向上一次反面向上的概率为________.

15.若不等式组无解，则的取值范围是_________.

16.如图，在中，Q是外一点，QA，QB与相切于A，B两点，点C，D是上的两点.若，则的度数为________.

17.圆锥的底面半径为5cm，高为12cm，则圆锥的侧面积是________.

18.如图，等边的边长为2，点Р为直线BC上的动点，把线段AP绕点A逆时针旋转60°至AE，点О为AB边上一动点，则OE的最小值为________.

19.如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕EF与AC相交于点О，连接BO.若，，则OB的长为_________.

20.如图，，正方形，正方形，正方形，正方形的顶点在射线上，顶点在射线ON上，连接交于点D，连接交于点，连接交于点，……连接交于点，连接交于点，……按照这个规律进行下去，设与的面积之和为，与的面积之和为，与的面积之和为，……，若，则_________.（用含有正整数的式子表示）

三、解答题（满分60分）

21.（本题5分）

先化简，再求值：，其中.

22.（本题6分）

如图，三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题.

（1）将先向右平移3个单位长度，再向下平移2个单位长度，画出经过两次平移后的，写出点，的坐标；

（2）将绕点逆时针旋转90°，画出旋转后的；

（3）求出（2）中线段在旋转过程中扫过的面积.

23.（本题6分）

如图，在平面直角坐标系中，抛物线与轴交于点，，与y轴交于点C，连接BC.

（1）求抛物线的函数表达式，并直接写出抛物线顶点Р的坐标；

（2）D是抛物线上位于第四象限内的一点，连接AD，E是AD的中点，连接BE，CE，直接写出面积的最小值.

24.（本题7分）

某校九年级有1200名学生，为了解在疫情严控的条件下九年级开学后学生的上学方式，随机调查了该年组部分学生上学方式（A.私家车；B.校车；C公交车；D自行车；E步行.每人只能从中选择一种），绘制成如图所示的两幅不完整的统计图和统计表，结合图中信息回答下列问题：

（1）这次调查的学生共有________名，________，________；

（2）补全条形统计图；

（3）请估计该校九年级学生步行上学的有多少名.

25.（本题8分）

某地区在同一直线上依次有甲、乙，丙三座城市，一列快车从甲市出发匀速行驶开往丙市，一列动车从丙市出发匀速行驶往返于乙、丙两座城市，两列火车同时出发，如图是两列火车距乙市的路程（单位：千米）与行驶时间（单位：小时）之间的函数图象，请你结合图象信息解决下列问题：

（1）甲、乙两市相距_________千米，动车的速度是________千米/小时，图象中的值为________；

（2）求动车从乙地返回过程中y与x之间的函数解析式，并直接写出自变量x的取值范围；

（3）请直接写出快车出发多长时间行驶中的两列火车相距30千米.

26.（本题8分）

已知四边形ABCD是菱形，点E，F分别在边AD，CD上，，.

（1）如图1，当时，易证：（不需证明）；

（2）当时，如图2；当，如图3，线段AE，CF，EF之间有怎样的数量关系?请直接写出你的猜想，并对图3加以证明.

27.（本题10分）

我市组织20辆汽车装运A，B，C三种水果共有100吨到外地销售.按计划20辆汽车都要装运，每辆汽车只能整吨装运同一种水果，且必须装满.

根据表格中提供的信息，解答以下问题：

（1）设有x辆车装运A种水果，有y辆车装运B种水果，求y与x之间的函数关系式；

（2）如果装运每种水果的车都不少于4辆，那么可以安排哪几种运输方案?

（3）在（2）的条件下，若要此次销售获利最大，应安排哪种方案?求出最大利润.

28.（本题10分）

如图，矩形OABC的边OA在x轴的正半轴上，OC在y轴的正半轴上，OA，OC的长是一元二次方程的实数根，且.过点B且垂直于直线OB的直线分别交x轴和y轴于点D，E，动点P以每秒5个单位长度的速度，从点O出发，沿射线OB的方向匀速运动，过点Р作轴于点M，轴交直线DE于点Q，过点Q作轴于点N.设四边形PQNM与重合部分的面积为S，点Р运动的时间为（，且）.

（1）求点D的坐标；

（2）求在点Р运动的过程中S与t之间的函数解析式；

（3）当时，射线PB上是否存在点R，使是等腰三角形?若存在，请直接写出点R的坐标；若不存在，请说明理由.

数学试题

一、选择题

1.C  2.B  3.A  4.A  5.B  6.C  7.C  8.B  9.A  10.B

二、填空题

11.   12.   13. （或等）

14.   15.   16.215°  17.   18.   19.   20.

三、解答题

21.原式

.

当时，原式.

22.解：（1）如图所示. ，.

（2）如图所示.

（3），

∴扫过的面积为 .

23.解：（1）∵抛物线，过点，.

∴解得

∴抛物线的函数表达式为

∴对称轴为直线

∴顶点的坐标为.

（2）过作轴交BC于F，如图

由（1）知抛物线的函数表达式为

∴设点的坐标为，

令，则，即

∵，E是AD的中点

∴点的坐标为，即

设直线BC的解析式为.

将，代入得

解得

∴直线的解析式为

∵轴，点E的横坐标为，

∴点的横坐标为，

∵点在直线上，∴点F的纵坐标为

∴，∴

∴

∴当时，取得最小值为.

24.解：（1）100，0.4，0.15.

（2）补图如图.

（3）1200×0.1=120（名）

25.解：（1）200，150，4.5.

（2）设动车从乙地返回的过程中y与x之间的函数解析式为.

把点和代入

得解得

答：动车从乙地返回的过程中y与x之间的函数解析式为.

（3）1.88小时或2.9小时或4.1小时.

26.解：（2）图2：.

图3：.

证明：如图3，将逆时针旋转30°至，连接.

∴，.

∵四边形ABCD是菱形，，

∴，.

∴.

∵，∴.

∴为等边三角形. ∴.

∵，∴.

∴，∴.

在和中，

∴.∴.

∴.

27.（1）根据题意，得.∴.

（2）解得.

∵为整数，∴可取整数为4，5，6，7，8.

共有五种方案如下：

方案一：4辆车装运A种水果，12辆车装运B种水果，4辆车装运C种水果；

方案二：5辆车装运A种水果，10辆车装运B种水果，5辆车装运C种水果；

方案三：6辆车装运A种水果，8辆车装运B种水果，6辆车装运C种水果；

方案四：7辆车装运A种水果，6辆车装运B种水果，7辆车装运C种水果；

方案五：8辆车装运A种水果，4辆车装运B种水果，8辆车装运C种水果.

（3）设获利为元.

.

∵，∴随x的增大而减小.

∴时，最大.

.

∴选择（2）中的方案一：4辆车装运A种水果，12辆车装运B种水果，4辆车装运C种水果，获利最多为140800元.

28.解：（1）由，得，

∵，∴，.

∵四边形是矩形，∴，.

∴.

∵，∴.

∴.∴.

∴，∴，∴.

∴，∴点的坐标为.

（2）①时，如图1.

∵，∴.

∴，∴.

∴，.

∵，∴.

∴.∴.

∵，∴.

∴.

∴；

②当时，

如图2，设PM与BD交于点T.同①理，

，，，

，.

∵，∴.

∴.∴.

∴.

∴.

综上，与之间的函数解析式为

（3）存在，，.