2022—2023学年人教版数学八年级下册平行四边形讲义

2022—2023学年人教版数学八年级下册平行四边形讲义　

平行四边形的概念：有两组对边分别平行的四边形叫平形四边形

平行四边形的性质: 1.平行四边形的对边平行且相等．

2.平行四边形的对角相等，邻角互补．

3.平行四边形的对角线互相平分。

平行四边形的计算： 面积=底×高

例题1： 1. 如图，AD∥BC，AE∥CD，BD平分∠ABC，

求证：AB=CE.

例题2：1.已知：如图，在平行四边形ABCD中，延长CB至E，延长AD至F，使得BE＝DF，连接EF与对角线AC交于点O．求证：OE＝OF．

1.已知：如图，□ABCD的对角线AC、BD相交于点O，EF过点O与AB、CD分别相交于点E、F.

求证：OE=OF，AE=CF，BE=DF.

2. 在平行四边形ACBO中，AO＝5，点B的坐标为（﹣2，4）.

（1）写出点A、C的坐标；

（2）求出平行四边形ACBO的面积.

平行四边形的判定

判定定理一：两组对边分别相等的四边形是平行四边形

判定定理二：两组对角分别相等的四边形是平行四边形

判定定理三：对角线互相平分的四边形是平行四边形

判定定理四：一组对边平行且相等的四边形是平行四边形

中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.

例题1：如图，平行四边形ABCD的对角线AC、BD交于点O, E、 F在AC上，G、H在BD上，且AE=CF, BG=DH

求证：四边形EGFH是平行四边形

例题2： 在中，对角线AC与BD交于O点，已知点E、F分别是AO、OC的中点，求证：四边形BFDE是平行四边形。

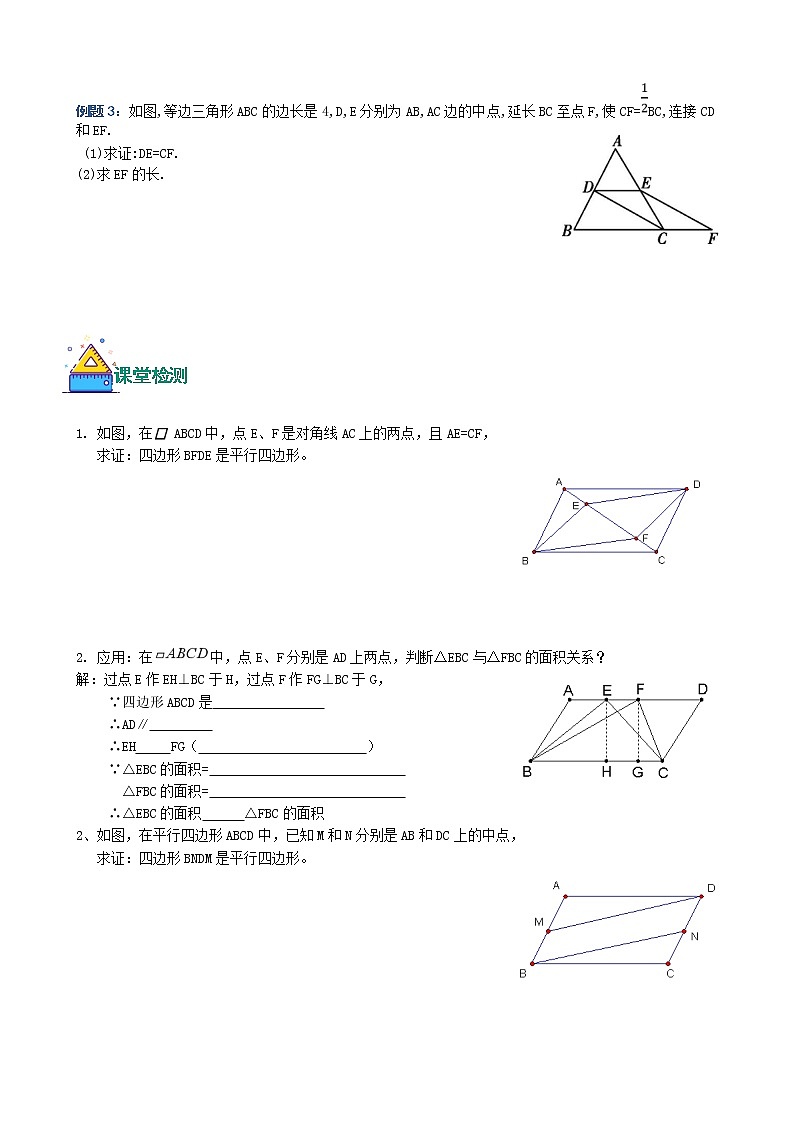
例题3：如图,等边三角形ABC的边长是4,D,E分别为AB,AC边的中点,延长BC至点F,使CF=BC,连接CD和EF.

 (1)求证:DE=CF.

(2)求EF的长.

1. 如图，在   ABCD中，点E、F是对角线AC上的两点，且AE=CF，

求证：四边形BFDE是平行四边形。

2. 应用：在中，点E、F分别是AD上两点，判断△EBC与△FBC的面积关系？

解：过点E作EH⊥BC于H，过点F作FG⊥BC于G，

∵四边形ABCD是               

∴AD∥        

∴EH     FG（                        ）

∵△EBC的面积=                           

  △FBC的面积=                           

∴△EBC的面积      △FBC的面积

2、如图，在平行四边形ABCD中，已知M和N分别是AB和DC上的中点，

求证：四边形BNDM是平行四边形。

3、如图 ，   ABCD中，AF＝CH， DE＝BG，

求证： EG和HF互相平分．

综合练习

1．如图，四边形ABCD中，∠B＝∠D，EF交CD于点G，交AD于点E，交BC的延长线于点F，∠DEF＝∠CFG．求证：四边形ABCD是平行四边形．

 2.如图，在四边形ABCD中，AC是对角线，AC＝AD，点E在边BC上，AB＝AE，∠BAE＝∠CAD，联结DE．

（1）求证：BC＝DE；

（2）当AC＝BC时，求证：四边形ABCD是平行四边形．

3．如图，E，F是▱ABCD对角线AC上的两点，AE＝FC．

（1）求证：四边形BFDE是平行四边形；

（2）若BE⊥AC，BE＝3，∠EBF＝60°，求EF的长．

5．如图，在▱ABCD中，AB＝12cm，BC＝6cm，∠A＝60°，点P沿AB边从点A开始以2cm/秒的速度向点B移动，同时点Q沿DA边从点D开始以1cm/秒的速度向点A移动，用t表示移动的时间（0≤t≤6）．

（1）当t为何值时，△PAQ是等边三角形？

（2）当t为何值时，△PAQ为直角三角形？