高中数学新教材选择性必修第三册课件+讲义 第7章 7.3.2 第1课时 离散型随机变量的方差

这是一份高中数学新教材选择性必修第三册课件+讲义 第7章 7.3.2 第1课时 离散型随机变量的方差，文件包含高中数学新教材选择性必修第三册第7章732第1课时离散型随机变量的方差pptx、高中数学新教材选择性必修第三册第7章732第1课时离散型随机变量的方差教师版docx、高中数学新教材选择性必修第三册第7章732第1课时离散型随机变量的方差学生版docx等3份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

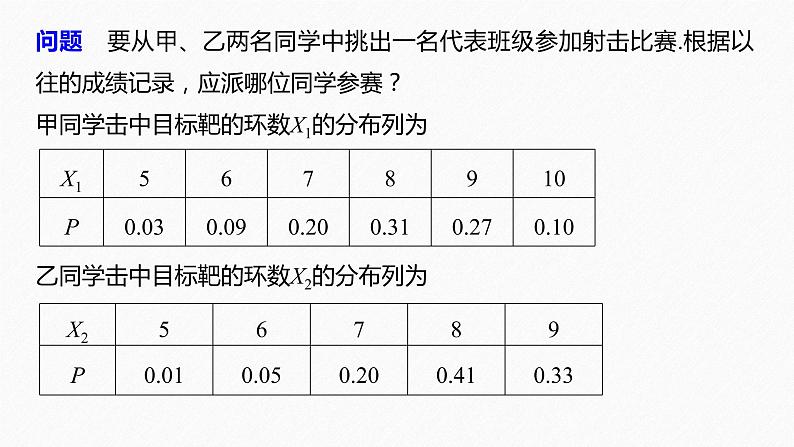
高中数学新教材同步课件选择性必修第三册 高考政策|高中“新”课程，新在哪里?1、科目变化：外语语种增加，体育与健康必修。第一，必修课程，由国家根据学生全面发展需要设置，所有学生必须全部修习、全部考试。第二，选择性必修课程，由国家根据学生个性发展和升学考试需要设置。第三，选修课程，由学校根据实际情况统筹规划开设，学生自主选择修习。2、课程类别变化，必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下，对原必修课程学分进行重构，由必修课程学分、选择性必修课程学分组成，适当增加选修课程学分。3、学时和学分变化，高中生全年假期缩减到11周。4、授课方式变化，选课制度将全面推开。5、考试方式变化，高考统考科目由教育部命题，学业水平合格性、等级性考试由各省命题。第1课时　离散型随机变量的方差第七章　7.3.2　离散型随机变量的方差1.理解离散型随机变量的方差及标准差的概念.2.能计算简单离散型随机变量的方差，并能解决一些实际问题.学习目标均值是离散型随机变量的一个特征数，它反映了离散型随机变量取值的平均水平，表示了随机变量在随机实验中取值的平均值，在初中我们也对一组数据的波动情况作过研究，即研究过一组数据的方差.本节我们将对反映随机变量取值的稳定与波动、集中与离散的程度的数字特征——方差进行研究.导语随堂演练课时对点练内容索引一、离散型随机变量的方差二、方差的计算三、方差的简单应用一、离散型随机变量的方差问题　要从甲、乙两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录，应派哪位同学参赛？ 甲同学击中目标靶的环数X1的分布列为乙同学击中目标靶的环数X2的分布列为提示　E(X1)＝8，E(X2)＝8，因为两个均值相等，所以只根据均值无法判断这两名同学的射击水平.可以利用样本方差，它可以刻画样本数据的稳定性.方差：设离散型随机变量X的分布列为考虑X所有可能取值xi与E(X)的偏差的平方(x1－E(X))2，(x2－E(X))2 ，…，(xn－E(X))2 ，因为X取每个值的概率不尽相同，所以我们用偏差平方关于取值概率的加权平均，来度量随机变量X取值与其均值E(X)的偏离程度，我们称D(X)＝ ＝______________为随机变量X的 ，有时也记为Var(X)，并称为随机变量X的 ，记为σ(X).注意点：一般地，随机变量的方差是非负常数.(x1－E(X))2 p1 ＋(x2－E(X))2 p2＋…＋(xn－E(X))2pn方差标准差例1　(多选)下列说法正确的是A.离散型随机变量的方差越大，随机变量越稳定B.若a是常数， 则D(a)＝0C.离散型随机变量的方差反映了随机变量偏离于均值的平均程度D.随机变量的方差和标准差都反映了随机变量取值偏离均值的平均程度， 方差或标准差越小，则偏离变量的平均程度越小√√√解析　随机变量的方差越小，随机变量越稳定.所以A错误.反思感悟　方差反应了随机变量取值的离散程度，方差或标准差越小，随机变量的取值越集中；方差或标准差越大，随机变量的取值越分散.跟踪训练1　(多选)下列说法中错误的是A.离散型随机变量X的均值E(X)反映了X取值的概率的平均值B.离散型随机变量X的方差D(X)反映了X取值的平均水平C.离散型随机变量X的均值E(X)反映了X取值的平均水平D.离散型随机变量X的方差D(X)反映了X取值的概率的平均值√√√解析　E(X)反映了X取值的平均水平，D(X)反映了X取值的离散程度.二、方差的计算例2　有10张卡片，其中8张标有数字2,2张标有数字5，从中随机地抽取3张卡片，设3张卡片数字之和为ξ，求E(ξ)和D(ξ).解　这3张卡片上的数字之和为ξ，ξ的可能取值为6,9,12.ξ＝6表示取出的3张卡片上均标有2，ξ＝9表示取出的3张卡片上两张标有2，一张标有5，ξ＝12表示取出的3张卡片上一张标有2，两张标有5，∴ξ的分布列为反思感悟　求离散型随机变量方差的步骤(1)理解随机变量X的意义，写出X的所有取值；(2)求出X取每个值的概率；(3)写出X的分布列；(4)计算E(X)；(5)计算D(X).跟踪训练2　(1)设离散型随机变量X的分布列为则D(X)等于√解析　由题意知，A.p1＝p4＝0.1，p2＝p3＝0.4B.p1＝p4＝0.4，p2＝p3＝0.1C.p1＝p4＝0.2，p2＝p3＝0.3D.p1＝p4＝0.3，p2＝p3＝0.2√解析　X的可能取值为1,2,3,4，四种情形的均值E(X)＝1×p1＋2×p2＋3×p3＋4×p4都为2.5，方差D(X)＝[1－E(X)]2×p1＋[2－E(X)]2×p2＋[3－E(X)]2×p3＋[4－E(X)]2×p4，A选项的方差D(X)＝0.65；B选项的方差D(X)＝1.85；C选项的方差D(X)＝1.05；D选项的方差D(X)＝1.45.所以选项B的情形对应样本的标准差最大.三、方差的简单应用例3　有甲、乙两种建筑材料，从中各取等量样品检查它们的抗拉强度如表所示：其中，ξA，ξB分别表示甲、乙两种材料的抗拉强度，在使用时要求抗拉强度不低于120，试比较甲、乙两种建筑材料的稳定程度(哪一个的稳定性较好).解　E(ξA)＝110×0.1＋120×0.2＋125×0.4＋130×0.1＋135×0.2＝125，E(ξB)＝100×0.1＋115×0.2＋125×0.4＋130×0.1＋145×0.2＝125.D(ξA)＝0.1×(110－125)2＋0.2×(120－125)2＋0.4×(125－125)2＋0.1×(130－125)2＋0.2×(135－125)2＝50，D(ξB)＝0.1×(100－125)2＋0.2×(115－125)2＋0.4×(125－125)2＋0.1×(130－125)2＋0.2×(145－125)2＝165.由此可见E(ξA)＝E(ξB)，D(ξA)E(η)，说明在一次射击中，甲的平均得分比乙高，但D(ξ)>D(η)，说明甲得分的稳定性不如乙，因此甲、乙两人技术水平都不够全面，各有优劣.1.知识清单：离散型随机变量的方差、标准差.2.方法归纳：公式法.3.常见误区：方差公式套用错误.课堂小结随堂演练1.已知随机变量X的分布列为P(X＝k)＝ ，k＝3,6,9，则D(X)等于A.6 B.9 C.3 D.41234√1234√解析　显然X服从两点分布，∴D(X)＝m(1－m).12343.设随机变量X的分布列为√123412344.已知离散型随机变量X的分布列如表所示，若E(X)＝0，D(X)＝1，则a＝______，b＝_____.课时对点练1.随机变量X的方差，反映其取值的A.平均水平 B.分布规律C.波动大小 D.最大值和最小值基础巩固12345678910111213141516√则D(ξ)等于2.已知随机变量ξ的分布列如下表：12345678910111213141516√现有一场比赛，应派哪位运动员参加较好A.甲 B.乙 C.甲、乙均可 D.无法确定3.由以往的统计资料表明，甲、乙两名运动员在比赛中的得分情况为：12345678910111213141516√解析　∵E(X1)＝E(X2)＝1.1，D(X1)＝1.12×0.2＋0.12×0.5＋0.92×0.3＝0.49，D(X2)＝1.12×0.3＋0.12×0.3＋0.92×0.4＝0.69，∴D(X1)D(X2)B.D(X1)＝D(X2)C.D(X1)D(X2).6.(多选)已知A1，A2为两所高校举行的自主招生考试，某同学参加每所高校的考试获得通过的概率均为 ，该同学一旦通过某所高校的考试，就不再参加其他高校的考试，设该同学通过考试的高校个数为随机变量X，则A.X的可能取值为0,1 B.X服从两点分布C.E(X)＝1 D.D(X)＝12345678910111213141516√√√12345678910111213141516解析　由已知X的可能取值为0,1.且服从两点分布.则a＝______，D(X)＝________.123456789101112131415167.已知随机变量X的分布列如表所示：解析　根据随机变量分布列的性质，知0.4＋0.1＋a＝1，所以a＝0.5，E(X)＝0.4＋0.3＋2.5＝3.2，D(X)＝2.22×0.4＋0.22×0.1＋1.82×0.5＝3.56.0.53.56123456789101112131415168.已知离散型随机变量X的可能取值为x1＝－1，x2＝0，x3＝1，且E(X)＝0.1，D(X)＝0.89，则对应x1，x2，x3的概率p1，p2，p3分别为______，______，______.0.40.10.5解析　由题意知，123456789101112131415169.某农场计划种植某种新作物，为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地，每大块地分为n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙.假设n＝4，在第一大块地中，种植品种甲的小块地的数目记为X，求X的分布列、均值及方差.12345678910111213141516解　X可能的取值为0,1,2,3,4，123456789101112131415161234567891011121314151610.为选拔奥运会射击选手，对甲、乙两名射手进行选拔测试.已知甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ，η，甲、乙两名射手在每次射击中击中的环数均大于6环，且甲射中10,9,8,7环的概率分别为0.5,3a，a,0.1，乙射中10,9,8环的概率分别为0.3,0.3,0.2.(1)求ξ，η的分布列；12345678910111213141516解　依据题意知，0.5＋3a＋a＋0.1＝1，解得a＝0.1.∵乙射中10,9,8环的概率分别为0.3,0.3,0.2，∴乙射中7环的概率为1－(0.3＋0.3＋0.2)＝0.2.∴ξ，η的分布列分别为12345678910111213141516(2)求ξ，η的均值与方差，并以此比较甲、乙的射击技术并从中选拔一人.解　结合(1)中ξ，η的分布列，可得E(ξ)＝10×0.5＋9×0.3＋8×0.1＋7×0.1＝9.2，E(η)＝10×0.3＋9×0.3＋8×0.2＋7×0.2＝8.7，D(ξ)＝(10－9.2)2×0.5＋(9－9.2)2×0.3＋(8－9.2)2×0.1＋(7－9.2)2×0.1＝0.96，D(η)＝(10－8.7)2×0.3＋(9－8.7)2×0.3＋(8－8.7)2×0.2＋(7－8.7)2×0.2＝1.21.∵E(ξ)＞E(η)，说明甲平均射中的环数比乙高.又∵D(ξ)＜D(η)，说明甲射中的环数比乙集中，比较稳定.∴甲的射击技术好.A.0个 B.1个 C.2个 D.3个综合运用1234567891011121314151611.已知随机变量ξ的分布列为√123456789101112131415161234567891011121314151612.(多选)已知随机变量X的分布列是√√√12345678910111213141516若E(ξ)＝2，则D(ξ)的最小值等于A.0 B.2 C.4 D.无法计算12345678910111213141516√13.已知随机变量ξ的分布列为12345678910111213141516即m＋2n＝6.当n＝2时，D(ξ)取得最小值，此时m＝2，不符合题意，故D(ξ)无法取得最小值.12345678910111213141516312345678910111213141516拓广探究1234567891011121314151615.编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的人数是ξ，则E(ξ)＝_____，D(ξ)＝_____.1112345678910111213141516解析　ξ的所有可能取值为0,1,3，ξ＝0表示三位同学全坐错了，有2种情况，即编号为1,2,3的座位上分别坐了编号为2,3,1或3,1,2的学生，ξ＝1表示三位同学只有1位同学坐对了，ξ＝3表示三位同学全坐对了，即对号入座，123456789101112131415161234567891011121314151616.某迷宫有三个通道，进入迷宫的每个人都要经过一扇智能门.首次到达此门，系统会随机(即等可能)为你打开一个通道，若是1号通道，则需要1小时走出迷宫；若是2号、3号通道，则分别需要2小时、3小时返回智能门.再次到达智能门时，系统会随机打开一个你未到过的通道，直至走出迷宫为止.令ξ表示走出迷宫所需的时间.(1)求ξ的分布列；12345678910111213141516解　ξ的所有可能取值为1,3,4,6，当ξ＝3时，先走2通道，再走1通道，当ξ＝4时，先走3通道，再走1通道，12345678910111213141516当ξ＝6时，先走2通道，再走3通道，最后再走1通道，或者先走3通道，再走2通道，最后再走1通道，所以ξ的分布列为12345678910111213141516(2)求ξ的均值和方差.