2022-2023学年小学五年级下册数学期中考试综合素养测评卷（A3版）（人教版）

这是一份2022-2023学年小学五年级下册数学期中考试综合素养测评卷（A3版）（人教版），共9页。试卷主要包含了考试结束后将试卷交回等内容，欢迎下载使用。
保密★启用前
2022-2023学年五年级下册数学期中考试综合素养测评卷
考试分数：100分；考试时间：90分钟
注意事项：
1．答题前，填写好自己的姓名、班级、考号等信息，请将答案写在规定的位置上。
2．选择题、判断题必须使用2B铅笔填涂答案，非选择、判断题必须使用黑色墨迹签字笔或钢笔答题，请将答案填写在规定的位置上。
3．考试结束后将试卷交回。

一、选择题（每题2分，共16分）
1．王叔叔晚上散步并从一个路灯下经过，下列描述他影子的长度变化合理的是（    ）。
A．越来越短 B．越来越长 C．不变 D．先变短再变长
2．如图是若干个小正方体堆成的几何体从正面和上面看到的图形，那么从左面看到的是（    ）。

A． B． C． D．
3．下面说法完全正确的是（    ）。
A．因为5×6＝30，所以5和6是因数，30是倍数
B．两个面积相等的三角形可以拼成一个平行四边形
C．自然数2既是偶数又是质数
D．一个数的末尾是0、3、6、9的数都是3的倍数
4．如果a是奇数，b是偶数，且a＜b，下列各式结果是奇数的是（    ）。
A．a＋a B．a×b C．b＋b D．b－a
5．图中，每个小正方体的体积是1dm3，大长方体的体积是（    ）。

A．20dm3 B．30dm3 C．36dm3 D．45dm3
6．如图，将下面的纸片折起来可以做成一个正方体，这个正方体的6号面的对面是（    ）号面。

A．4 B．3 C．1 D．5
7．一筐苹果，3个一拿，4个一拿，5个一拿都正好拿完没有余数。这筐苹果最少应有（    ）个。
A．30 B．60 C．90 D．120
8．将一个长24厘米，宽18厘米的长方形纸剪成若干个面积相等的正方形，要求没有剩余且正方形的面积最大，每个正方形的面积是（    ）平方厘米。
A．6 B．24 C．36 D．96
二、填空题（每题2分，共16分）
9．玲玲借助长方体体积计算方法，巧妙的测出了一块石头的体积，如图，石头的体积是( )立方厘米。

10．用5个同样的小正方体，摆出从正面看是的图形，有( )种摆法。
11．如果a是一个不为0的自然数，那么2a一定是( )数，2a＋1一定是( )数。（选填“奇”或“偶”）
12．一个数既是6的倍数，又是24的因数，这个数可能是( )或( )。
13．一个正方体的棱长是4厘米，把它分成两个同样的长方体，表面积增加( )平方厘米。
14．将一副扑克牌（去除大、小王）反扣在桌面上，从中任意抽取一张，抽到“6”的可能性是( )，抽到“红心”牌的可能性是( )。（填写最简分数）
15．将一根20米长的铁丝剪4次等分成相同的小段，每段铁丝长( )米，每段铁丝占全长的( )。
16．一个立体图形，从左面和前面看都是，搭这样的立体图形至少需要( )个正方体，最多需要( )个正方体。
三、判断题（每题2分，共8分）
17．一个数，如果只有1和它本身两个因数，那么这样的数叫做质数。( )
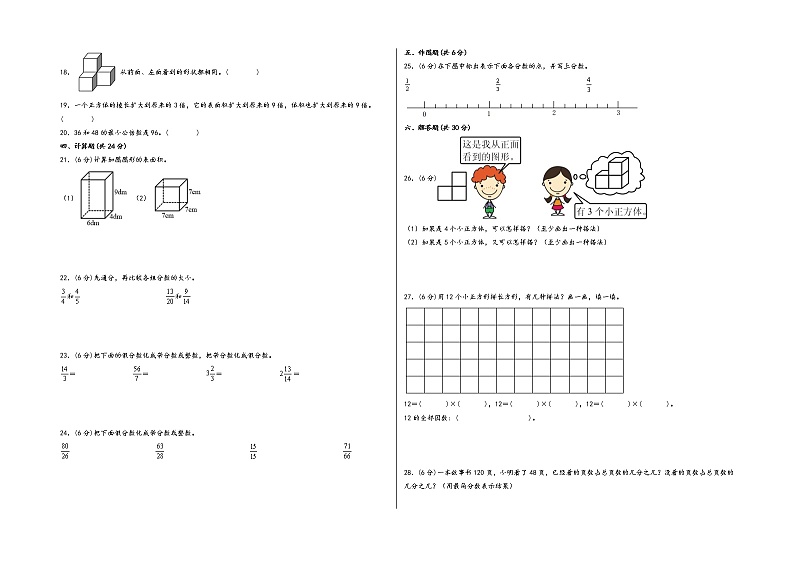
18．从前面、左面看到的形状都相同。( )
19．一个正方体的棱长扩大到原来的3倍，它的表面积扩大到原来的9倍，体积也扩大到原来的9倍。( )
20．36和48的最小公倍数是96。( )
四、计算题(共24分)
21．(6分)计算如图图形的表面积。
（1）（2）



22．(6分)先通分，再比较各组分数的大小。
和            和



23．(6分)把下面的假分数化成带分数或整数，把带分数化成假分数。
＝        ＝        ＝        ＝



24．(6分)把下面假分数化成带分数或整数。
                                    



五、作图题(共6分)
25．(6分)在下图中标出表示下面各分数的点，并写上分数。
                        

六、解答题(共30分)
26．(6分)
（1）如果是4个小正方体，可以怎样搭？（至少画出一种搭法）
（2）如果是5个小正方体，又可以怎样搭？（至少画出一种搭法）



27．(6分)用12个小正方形拼长方形，有几种拼法？画一画，填一填。

12＝( )×( )，12＝( )×( )，12＝( )×( )。
12的全部因数：( )。



28．(6分)一本故事书120页，小明看了48页，已经看的页数占总页数的几分之几？没看的页数占总页数的几分之几？（用最简分数表示结果）



29．(6分)一个长方体水箱，里面长14厘米、宽10厘米、深16厘米，给里面加入10厘米深的水（如下图 a），贝贝将一块石头放入水中后，水面比原来上升2.5厘米（如下图 b）。求石头的体积是多少？




30．(6分)用一根铁丝刚好焊成一个棱长8厘米的正方体框架，如果用这根铁丝焊成一个长9厘米、宽8厘米的长方体框架，它的高应该是多少厘米？






















































参考答案
1．D
【分析】人距光源越近，影子就越短，反之，影子就越长，据此解答。
【详解】王叔叔晚上散步并从一个路灯下经过，下列描述他影子的长度变化合理的是先变短再变长。
故答案为：D
【点睛】物体距光源越近，影子越短，距光源越远，影子越长，如早晚距太阳远，物体的影子就长，中午距太阳近，影子就短。
2．A
【分析】根据从不同方向观察几何体的方法，这个几何体从正面看有4个小正方体，结合从上面看到的图形，这个几何体应该摆成：，再从左面观察，即可得解。
【详解】根据分析得，这个几何体的摆法如图：，那么从左面观察，得到的图形应该是。
故答案为：A
【点睛】本题考查从不同的方向观察物体，解答本题的关键是掌握根据物体三视图确定物体形状的方法。
3．C
【分析】（1）在整数除法中，如果商是整数而没有余数，我们就说被除数是除数和商的倍数，除数和商是被除数的因数；
（2）由三角形的面积推导公式可知，两个完全相同的三角形可以拼成一个平行四边形，三角形的面积相等时形状不一定完全相同；
（3）整数中，是2的倍数的数叫做偶数（0也是偶数），不是2的倍数的数叫做奇数；一个数，如果只有1和它本身两个因数，那么这样的数叫做质数；一个数，如果除了1和它本身还有别的因数，那么这样的数叫做合数；
（4）3的倍数特征：各个位上数字相加的和是3的倍数，据此解答。
【详解】A．5×6＝30，则30÷5＝6，所以5和6是30的因数，30是5和6的倍数。
B．
如图所示，三角形甲和三角形乙等底等高，则它们的面积相等，但是它们的形状不相同，所以三角形甲和三角形乙不能拼成一个平行四边形。
C．2是2的倍数，则2是偶数，2的因数只有1和2，则2也是质数，所以自然数2既是偶数又是质数。
D．分析可知，3的倍数和各个位上的数字之和有关，与这个数的尾数无关，如：13的末尾是3，但13是一个质数，13不是3的倍数。
故答案为：C
【点睛】掌握因数、倍数、质数、合数的意义，以及三角形的面积推导公式和3的倍数特征是解答题目的关键。
4．D
【分析】根据：奇数＋奇数＝偶数，奇数×偶数＝偶数，偶数＋偶数＝偶数，奇数－偶数＝奇数，偶数－奇数＝奇数；据此解答。
【详解】A．a是奇数，a＋a的结果是偶数；
B．a是奇数，b是偶数，a×b的结果是偶数；
C．b是偶数，b＋b的结果是偶数；
D．a是奇数，b是偶数，且a＜b，b－a的结果是奇数；
故答案为：D
【点睛】此题考查了奇数、偶数的判断，可以运用公式判断，也可以用列数计算再判断，关键熟记概念。
5．D
【分析】通过观察图形可知，沿长方体的长摆了5个小正方体，沿宽摆了3行，沿高摆了3层，根据长方体的体积＝长×宽×高，求出一共摆了多少个小正方体，然后再乘每个小正方体的体积即可。
【详解】1×（5×3×3）
＝1×（15×3）
＝1×45
＝45（dm3）
大长方体的体积是45dm3。
故答案为：D
【点睛】此题考查的目的是理解掌握长方体体积公式的推导过程及应用。
6．A
【分析】根据正方体展开图的11种特征，属于“1－3－2”型，折叠成一个正方体后，1号面和5号面相对，2号面和3号面相对，4号面和6号面相对，据此解答。
【详解】由分析可得：这个正方体的6号面的对面是4号面。
故答案为：A
【点睛】此题考查了正方体的展开图。
7．B
【分析】根据题意：一筐苹果，3个一拿，4个一拿，5个一拿都正好拿完而没有余数，说明这框苹果是3、4、5的倍数，所以只要求出3、4、5的最小公倍数，即可得解。
【详解】因为3、4、5两两互质，所以3、4、5的最小公倍数是：
3×4×5
＝12×5
＝60（个）
一筐苹果，3个一拿，4个一拿，5个一拿都正好拿完没有余数，这筐苹果最少应有60个；
故答案为：B
【点睛】考查了灵活运用求几个数的最小公倍数的方法来解决实际问题。
8．C
【分析】根据题意，剪成的最大正方形的边长是24厘米和18厘米的最大公因数。据此，先将24和18分解质因数，计算出公有质因数的乘积，即24和18的最大公因数，即正方形的边长。正方形面积＝边长×边长，将数据代入求出每个正方形的面积即可。
【详解】24＝2×2×2×3
18＝2×3×3
2×3＝6
所以，24和18的最大公因数是6，每个正方形的边长是6厘米。
6×6＝36（平方厘米）
所以，每个正方形的面积是36平方厘米。
故答案为：C
【点睛】本题考查了最大公因数和正方形的面积，掌握最大公因数的求法、正方形的面积公式是解题关键。
9．1000
【分析】根据题意，把石头放到容器中，水上升了（12－10）厘米，石头的体积等于水面上升的体积，根据长方体的体积公式：V＝abh，把数据代入公式解答。
【详解】25×20×（12－10）
＝500×2
＝1000（立方厘米）
即石头的体积是1000立方厘米。
【点睛】此题考查的目的是理解掌握不规则物体的体积的计算方法利用排水法，根据长方体的体积公式解答。
10．21
【分析】先用3个同样的小正方体，摆出从正面看是的图形，另外2个分三种情况进行摆放：第一种情况2个一起同一列放在三个小正方形的前面或者后面，有6种摆法；第二种情况2个同一行放在放在三个小正方形的前面或者后面，有6种摆法；第三种情况2个一前一后分开摆放，有9种摆法，一共6＋6＋9＝21（种），据此填空即可。
【详解】由分析可知：用5个同样的小正方体，摆出从正面看是的图形，有21种摆法。
摆放方式如下图：

【点睛】掌握根据三视图还原图形的方法是解题的关键。
11．     偶     奇
【分析】整数中，是2的倍数的数叫偶数，不是2的倍数的数叫奇数。如果a是一个不为0的自然数，那么2a一定是2的倍数，也就是偶数；2a＋1不是2的倍数，一定是奇数。
【详解】举例判断：
当a＝1时，2a＝2×1＝2，是偶数
2a＋1＝2＋1＝3，是奇数
【点睛】此题考查用字母表示数以及奇数偶数的判断。
12．     6     12
【分析】24以内的6的倍数有；6，12，18，24；24的因数且大于等于6的有：6，8，12，24，看两组数据中重复的数据即为答案。
【详解】24（包括）以内6的倍数有：6、12、18、24，因为18不是24的因数，所以一个数既是6的倍数，又是24的因数，这个数可能是6、12、24。
【点睛】本题主要考查的是因数和倍数的求解，解题的关键是熟练掌握因数、倍数的意义及应用，进而得出答案。
13．32
【分析】将一个正方体分成两个完全相同的长方体，需要切一刀，增加两个面的面积，每一个面的面积为4×4＝16平方厘米。
【详解】2×（4×4）
＝2×16
＝32（平方厘米）
表面积增加32平方厘米。
【点睛】明确切一刀会增加两个面是解题的关键。
14．         
【分析】由题意可知，用6的张数除以总张数，就是抽到6的可能性是几分之几；用“红心”牌张数除以总张数，就是抽到“红心”牌可能性是几分之几。6共有4张，一副扑克牌（去除大、小王）共有52张；“红心”牌的张数共有13张。据此解答即可。
【详解】4÷52＝
13÷52＝
则抽到“6”的可能性是，抽到“红心”牌的可能性是。
【点睛】本题考查分数与除法，明确分数与除法的关系是解题的关键。
15．     4    
【分析】将一根铁丝剪4次等分成相同的小段，根据平均分的段数＝剪的次数＋1，每段铁丝的长度＝铁丝的总长度÷平均分的段数，用20÷（4＋1）即可求出每段的长度；把全长看作单位“1”，平均分成（4＋1）段，则每段占全长的。据此解答。
【详解】20÷（4＋1）
＝20÷5
＝4（米）
1÷（4＋1）
＝1÷5
＝
将一根20米长的铁丝剪4次等分成相同的小段，每段铁丝长4米，每段铁丝占全长的。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”，求分率：平均分的是单位“1”；求具体的数量：平均分的是具体的数量，要注意：分率不能带单位名称，而具体的数量要带单位名称。
16．     3     5
【分析】根据从左面和前面看到的形状可知：该几何体下层至少2个小正方体，分两行，前面一行1个，右齐，后面一行1个，左齐；最多4个，分两行，每行2个。上层1个，在第二行左齐，据此解答。
【详解】2＋1＝3（个）
4＋1＝5（个）
搭这样的立体图形至少需要3个正方体，最多需要5个正方体。
【点睛】本题是考查从不同方向观察物体和几何图形，关键是培养学生的观察能力。
17．√
【详解】根据质数的定义可知，一个数，如果只有1和它本身两个因数，那么这样的数叫做质数。比如5的因数只有1和5，所以5是质数。原题说法正确。
故答案为：√
18．√
【分析】观察图形可知，该立体图形从前面和左面看到的形状都是有两层，第一层有2个小正方形，第二层有1个小正方形，左齐。据此进行判断即可。
【详解】由分析可知：
从前面、左面看到的形状都相同。原题干说法正确。
故答案为：√
【点睛】本题考查观察物体，明确从不同方向观察到的形状是解题的关键。
19．×
【分析】正方体表面积＝棱长×棱长×6，正方体体积＝棱长×棱长×棱长，正方体棱长扩大到原来的几倍，表面积扩大到原来的倍数×倍数，体积扩大到原来的倍数×倍数×倍数，据此分析。
【详解】3×3＝9
3×3×3＝27
一个正方体的棱长扩大到原来的3倍，它的表面积扩大到原来的9倍，体积扩大到原来的27倍，所以原题说法错误。
故答案为：×
【点睛】关键是掌握并灵活运用正方体表面积和体积公式，根据积的变化规律进行分析。
20．×
【分析】求几个数的最小公倍数的方法：这几个数的公有的因数和它们独有的质因数的连乘积就是它们的最小公倍数，由此可以解得。
【详解】36＝2×2×3×3
48＝2×2×2×2×3
所以36和48的最小公倍数是2×2×2×2×3×3＝144，所以原题计算错误。
故答案为：×
【点睛】此题考查了求几个数的最小公倍数的方法，由此可以解决。
21．（1）228dm2；（2）294cm2
【分析】长方体表面积＝（长×宽＋长×高＋宽×高）×2，正方体表面积＝棱长×棱长×6，将数据代入公式，求出图形的表面积即可。
【详解】（1）（6×4＋6×9＋4×9）×2
＝（24＋54＋36）×2
＝114×2
＝228（dm2）
（2）7×7×6＝294（cm2）
22．＜；＞
【分析】把异分母分数化成和原来分数相等的同分母分数，叫做通分；
异分母异分子分数比较大小，先通分，变成分母相同而大小不变的分数，再比较大小；
分数比较大小：分母相同，分子大的，分数就大。
【详解】（1）＝＝
＝＝
因为＜，所以＜；
（2）＝＝
＝＝
因为＞，所以＞。
23．；8；；
【分析】假分数化成整数或带分数的方法：用假分数的分子除以分母，如果分子是分母的倍数，所得的商就是整数；如果分子不是分母的倍数，所得的商就是带分数的整数部分，分母不变，余数做分数部分的分子；据此进行互化即可。
【详解】＝
＝8
＝
＝
24．；；1；
【分析】不是最简分数的，先运用分数的基本性质化简成最简分数。
把假分数化成带分数的方法：用分子除以分母，得到的商和余数；商是带分数的整数部分，余数是带分数的分子，分母不变。
当假分数的分子为分母的倍数时，能化成整数。
【详解】＝＝40÷3＝
＝＝9÷4＝
＝15÷15＝1
＝71÷66＝
【点睛】掌握假分数与带分数的互化是解题的关键。
25．见详解
【分析】根据题图可知，数轴上把一个单位长度平均分成6份，每份是，几份就是几个，利用分数的基本性质，把几个分数化成分母是6的分数，＝，有3个；＝，有4个；＝，有8个；据此画图即可。
【详解】如图：

【点睛】此题考查了用数轴来表示分数，关键是看每小格表示的分数是多少。
26．（1）（2）见详解
【分析】（1）从正面观察，图形是，则第一行有2个小正方形，第二行有1个小正方形，共有3个小正方体，要用4个小正方体组成这个几何体，可把另一个小正方体放在第一行的前面或者后面即可满足题意；
（2）从正面观察，图形是，则第一行有2个小正方形，第二行有1个小正方形，共有3个小正方体，要用5个小正方体组成这个几何体，可把另外两个小正方体放在第一行的前面或者后面即可满足题意；
【详解】（1）如图，可以这样搭：、、、；
（2）如图，可以这样搭：、。
【点睛】本题考查从不同的方向观察物体，解答本题的关键是掌握根据物体三视图确定物体形状的方法。
27．     1     12     4     3     2     6     1、2、3、4、6、12
【分析】按照长×宽＝12，可得12＝12×1，即长摆12个，宽摆1个；12＝6×2，即长摆6个，宽摆2个；12＝4×3，即长摆4个，宽摆3个，所以12个正方形可以摆3种不同形式的长方形。
【详解】12＝1×12
12＝2×6
12＝3×4

12的全部因数：1、2、3、4、6、12。
【点睛】此题主要考查长方形的面积公式，主要利用长方形的面积等于12个正方形的面积。
28．已经看的页数占总页数的，没看的页数占总页数的
【分析】根据题意，利用看了的页数除以总页数，没看的页数除以总页数即可解答。
【详解】已看：48÷120＝
未看：（120－48）÷120
＝72÷120
＝
答：已经看的页数占总页数的，没看的页数占总页数的。
【点睛】本题考查一个数占另一个数的几分之几是多少，用除法计算。
29．350立方厘米
【分析】根据题意，将一块石头放入水中后，水面比原来上升2.5厘米，那么石头的体积等于水面上升部分的体积；水面上升部分是一个长14厘米、宽10厘米、高2.5厘米的长方体，根据长方体的体积＝长×宽×高，代入数据计算，即可求出这块石头的体积。
【详解】14×10×2.5
＝140×2.5
＝350（立方厘米）
答：石头的体积是350立方厘米。
【点睛】本题考查不规则物体体积的求法，明确放入石头的体积等于水面上升部分的体积，然后利用长方体的体积公式解答。
30．7厘米
【分析】正方体棱长和＝棱长×12，长方体棱长和＝（长＋宽＋高）×4。据此，先求出这个正方体框架的棱长和，即后面焊成的长方体框架的棱长和。将长方体的棱长和除以4，再减去长和宽，即可求出它的高。
【详解】8×12÷4－9－8
＝96÷4－9－8
＝24－9－8
＝7（厘米）
答：它的高是7厘米。
【点睛】本题考查了长方体和正方体的棱长和，熟练运用棱长和公式是解题的关键。