

2023年河南省湘豫名校联考高考物理一模试卷(含答案解析)
展开2023年河南省湘豫名校联考高考物理一模试卷
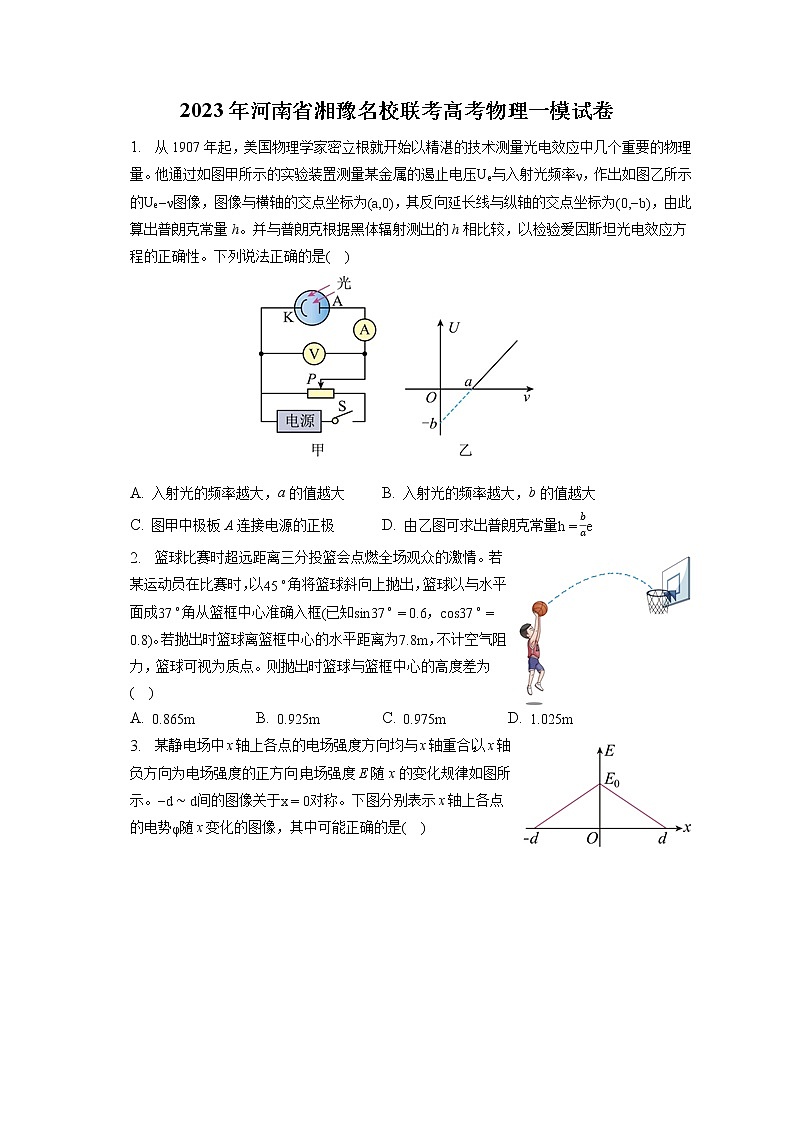
1. 从1907年起,美国物理学家密立根就开始以精湛的技术测量光电效应中几个重要的物理量。他通过如图甲所示的实验装置测量某金属的遏止电压Ue与入射光频率ν,作出如图乙所示的Ue−ν图像,图像与横轴的交点坐标为(a,0),其反向延长线与纵轴的交点坐标为(0,−b),由此算出普朗克常量h。并与普朗克根据黑体辐射测出的h相比较,以检验爱因斯坦光电效应方程的正确性。下列说法正确的是( )
A. 入射光的频率越大,a的值越大 B. 入射光的频率越大,b的值越大
C. 图甲中极板A连接电源的正极 D. 由乙图可求出普朗克常量h=bae
2. 篮球比赛时超远距离三分投篮会点燃全场观众的激情。若某运动员在比赛时,以45∘角将篮球斜向上抛出,篮球以与水平面成37∘角从篮框中心准确入框(已知sin37∘=0.6,cos37∘=0.8)。若抛出时篮球离篮框中心的水平距离为7.8m,不计空气阻力,篮球可视为质点。则抛出时篮球与篮框中心的高度差为( )
A. 0.865m B. 0.925m C. 0.975m D. 1.025m
3. 某静电场中x轴上各点的电场强度方向均与x轴重合,以x轴负方向为电场强度的正方向,电场强度E随x的变化规律如图所示。−d∼d间的图像关于x=0对称。下图分别表示x轴上各点的电势φ随x变化的图像,其中可能正确的是( )
A. B.
C. D.
4. 科学家探测到一颗离地球距离最近的人类易居行星,测得该行星的密度为ρ,半径为R,已知引力常量为G,若在该行星上发射一颗卫星绕其做圆周运动。下列关于该卫星运行的物理量,描述错误的是( )
A. 卫星的最大运行速度大小为 4ρGπR23
B. 卫星的最大加速度大小为4ρGπR3
C. 卫星的最大运行角速度为 4πρG3
D. 卫星与行星中心连线单位时间内扫过的最小面积为R2 43πρG
5. 如图所示,四条长度相等的长直导线a、b、c、d分别处在正方形的四个顶点上,垂直于正方形平面固定放置,O为正方形的中心。现给四条导线通入大小相等的恒定电流,a、b两导线中电流的方向垂直纸面向里,c、d两导线中电流的方向垂直纸面向外。则下列说法正确的是( )
A. 导线a和导线b受到的安培力相同
B. 导线a和导线c受到的安培力方向相反
C. O点磁场的磁感应强度方向垂直bc向下
D. 若保持b、c两导线中电流大小不变,方向反向,则O点磁场的磁感应强度方向转过90∘
6. 在如图所示的理想变压器电路中,变压器原,副线圈的匝数比为2:1,定值电阻R1=5Ω、R2=1Ω,R3为电阻箱。在a、b端输入正弦交变电压u=10 2sin100πt(V),通过调节电阻箱R3的阻值,来改变变压器的输出功率。下列说法正确的是( )
A. 当变压器输出功率最大时,变压器副线圈两端的电压为5V
B. 当变压器输出功率最大时、电阻箱接入电路的电阻为0.25Ω
C. 当变压器输出功率最大时,变压器输出的最大功率为5W
D. 当变压器原线圈中的电流分别为0.5A、1.5A时,变压器的输出功率相等
7. 如图所示,直角三角形单匝金属线框ABC放在光滑绝缘水平面上,∠B=90∘,∠C=30∘,BC边长为L,金属线框ABC的电阻为R。有界匀强磁场垂直于水平面向上,磁感应强度大小为B,磁场平行边界MN、PQ的间距为12L。现给金属线框ABC一个瞬时冲量,使金属线框ABC获得一向右的速度v,同时给金属线框ABC施加外力F(大小、方向未知)使金属线框ABC保持速度v匀速通过磁场,金属线框ABC通过磁场的过程中BC边始终垂直于MN。从C点进入磁场开始,下列说法正确的是( )
A. 第一个L2v时间内,作用在金属线框ABC上的外力F的大小与时间成正比
B. 第一个L2v时间内,A、B两端的电压与时间成正比
C. 第二个L2v时间内,金属线框ABC中的电流随时间均匀增大
D. 第三个L2v时间内,通过金属线框ABC截面的电荷量为 3BL28R
8. 如图所示,质量均为m的物块A、B用轻弹簧连接并竖直放置,轻绳绕过分别固定在同一水平面上O、E两点的定滑轮一端与物块A相连,另一端与质量为12m的小球C相连,小球C套在水平固定、粗细均匀的光滑直杆上。开始时,小球C锁定在直杆的P点,连接小球的轻绳与水平方向的夹角为θ=53∘,物块B对地面的压力恰好为零。某时刻解除对小球C的锁定,同时对小球C施加一个水平向右、大小为F的恒力,小球C运动到直杆Q点时的速度达到最大,OQ与水平方向的夹角也为θ,D点为P、Q两点的中点,P、Q两点间的距离为L,E点在物块A的正上方,小球C运动过程中轻绳始终处于拉直状态,弹簧始终在弹性限度内。忽略两定滑轮的大小,已知重力加速度大小为g,sin53∘=45,cos53∘=35。下列说法正确的是( )
A. 小球C从P点运动到D点的过程中,合外力对物块A做的功为零
B. 小球C从P点运动到D点的过程中,弹簧的弹力和轻绳的拉力对物块A冲量的和为零
C. 小球C运动到Q点时物块A的速度大小为 8FL5m
D. 小球C运动到Q点时物块A的加速度大小为|5F3m−2g|
9. 某同学利用如图甲所示的实验装置探究物体的加速度与质量的关系。
(1)按正确的实验操作(包括平衡摩擦力)后,打出一条如图乙所示的纸带,图中A、B、C为三个相邻的计数点,若相邻计数点间的时间间隔为T,A、B两点间的距离为x1、A、C两点间的距离为x2,则小车的加速度为a=______ (用题目中给出物理量的字母表示)。
(2)改变小车中砝码的质量,重复操作,得到多条纸带。记下小车中的砝码质量m,利用纸带测量计算小车的加速度a。以m为纵坐标,以1a为横坐标,在坐标纸上作出的m−1a关系图像是一条倾斜的直线,如图丙所示。如果在误差允许的范围内,测得图中直线的斜率等于______ ,在纵轴上的截距绝对值b等于______ ,表明合外力一定时,加速度与质量成反比。(以上两空用文字表述)
10. 要测量两节新干电池的电动势和内阻,某实验小组根据实验室提供的器材连接成了如图所示的实验电路,其中定值电阻R0=2Ω,两个电压表的内阻都很大。
(1)实验器材中两个电压表的量程不同,其中一个量程为3V,另一个电压表的量程稍小,则量程为3V的电压表是______ (填“V1”或“V2”),闭合开关S前,应将滑动变阻器的滑片移到最______ (填“左”或“右”)端。
(2)闭合开关S后,移动滑动变阻器的滑片,测出多组电压表V1和电压表V2的示数U1、U2,在坐标系中描点作U2−U1图象,测得图象的斜率为0.56,图象与纵轴的截距为1.26V,则电池组的电动势E为______ V,电池组的内阻r为______ Ω。(结果均保留三位有效数字)
(3)由于电压表______ (填“V1”、“V2”或“V1和V2”)的分流,使测得的电池组的电动势比真实值______ (填“大”或“小”)。
11. 如图甲所示,质量为M=3kg的长木板ABC静止在足够长的光滑水平面上,长木板ABC的上表面由半径为R(未知)的光滑四分之一圆弧面AB和长为L=1m的粗糙水平面BC平滑连接而成,B为圆弧面AB的最低点且切线水平,水平面BC的C端固定一挡板。现将质量为m=1kg的物块从A点由静止释放,物块与挡板碰撞后相对木板向左运动到B点时与长木板相对静止。已知物块在木板BC间运动的过程中,受到的摩擦力F随物块距B点的距离x变化规律如图乙所示,物块与挡板碰撞过程的时间极短且没有机械能损失,重力加速度大小g取10m/s2,不计物块的大小。求:
(1)圆弧面AB的半径;
(2)物块从A点由静止释放到与长木板相对静止于B点,长木板运动的位移大小;
(3)物块与挡板碰撞后的瞬间,物块与长木板的速度大小。
12. 如图所示,在平面直角坐标系xOy的第一、二象限内存在电场方向沿y轴负方向的匀强电场区域Ⅰ,在y=−L下方存在电场方向沿y轴方向的匀强电场区域Ⅱ,在x轴下方和y=−L之间(含边界)存在垂直坐标系xOy平面向外的匀强磁场。在坐标为(−2L,L)的P点沿x轴向射出一个质量为m、电荷量为q(q>0)的带电粒子,粒子经电场区域偏转后从坐标原点O射出电场区域I。已知电场区域Ⅱ的电场强度是区域Ⅰ电场强度的2倍,粒子射出时的初速度大小为v0,不计粒子的重力大小。
(1)求匀强电场区域Ⅰ的电场强度大小;
(2)若粒子恰好不能进入匀强电场区域Ⅱ,求匀强磁场的磁感应强度的大小;
(3)若粒子经磁场偏转后恰好从y轴上坐标为(0,−L)的Q点进入匀强电场区域Ⅱ,求粒子第n次经过x轴的位置离P点的水平距离,及从P点射出到第n次经过x轴时,粒子运动的时间。
13. 下列说法正确的是( )
A. 晶体一定具有固定的熔点,但不一定具有规则的几何外形
B. 降低温度能够使气体的饱和气压降低,从而使气体液化
C. 一定质量的理想气体等压膨胀过程中一定从外界吸收热量
D. 当两分子间的作用力表现为斥力时,分子间的距离越大,分子势能越大
E. 一定量的理想气体,如果体积不变,分子每秒平均碰撞器壁次数随着温度的降低而增大
14. 如图所示,粗细均匀的U形玻璃管左管封闭、右管开口,右管内有一轻质活塞,活塞和A、B两段水银柱封闭着1、2两段理想气体。初始时,长为10cm的水银柱A下端与活塞下端平齐,水银柱B在左管中的液面比右管中的液面低10cm,气柱1长为10cm。现用外力缓慢向下压活塞,直至水银柱B在左管和右管中液面相平并稳定,已知大气压强为75cmHg,求:
(1)稳定后,A段水银对左管上封口处玻璃的压强大小;
(2)此过程中活塞下降的高度。(结果均保留两位小数)
15. 如图所示,一列简谐波沿x轴传播,t=0.2s时刻,x=−1m与x=1.5m间的波形如图所示,质点P平衡位置的坐标为x=−1m。已知质点P的振动方程为y=−10sin5πt(cm),则下列说法正确的是( )
A. 波沿x轴负方向传播
B. 波的传播速度大小为5m/s
C. 从图示时刻开始,经过1s,质点P运动的路程为50cm
D. t=0.4s时刻,质点P的位移为10cm
E. t=0.4s至t=0.6s时间内,质点P的速度先减小后增大
16. 如图所示,边长为L的正方形ABCD为一玻璃砖的截面,一束单色光从与AB边成30∘角的方向斜射到玻璃砖截面AB边上的E点。光束进入玻璃砖后经BC边反射后的反射光刚好射到CD边的中点F。已知EB=14L,光在真空中的传播速度为c。
(1)求玻璃砖对光的折射率。
(2)试判断光射到BC边时能否发生全反射,并求光从E点传播到F点所用的时间。
答案和解析
1.【答案】D
【解析】解:A.根据爱因斯坦光电效应方程Ek=hν−W0
又eUe=Ek
得Ue=heν−W0e
横轴截距a=W0h=ν0,即截止频率,为定值,与入射光的频率无关,故A错误;
B.纵轴截距−b=−W0e,为定值,与入射光的频率无关,故B错误;
C.由题可知,光电管上所加的电压为反向电压,所以图甲中极板A连接电源的负极,故C错误;
D.图像斜率k=he=ba,得h=bae,故D正确。
故选:D。
根据光电效应方程得出遏止电压与入射光频率的关系,通过图线的斜率求出普朗克常量;电压为零时,入射光的频率等于截止频率。
解决本题的关键掌握光电效应方程以及最大初动能与遏止电压的关系.
2.【答案】C
【解析】解:篮球的运动为斜抛运动,水平方向为匀速直线运动,竖直方向为竖直上抛运动,根据题意有:tan45∘=vyvx
水平方向x=vxt
竖直方向−vy′=vy−gt
篮球入框时,有:tan37∘=vy′vx
代入数据联立解得:t= 273200s
vx=vy=407 273200m/s
则抛出时篮球与篮框中心的高度差为y=vyt−12gt2
代入数据解得:y=0.975m
故C正确,ABD错误。
故选:C。
篮球的运动为斜抛运动,水平方向为匀速直线运动,竖直方向为竖直上抛运动,根据运动学公式列式求解即可。
本题考查斜抛运动,解题关键是将篮球的运动分解到水平方向和竖直方向,结合运动学公式列式求解即可。
3.【答案】C
【解析】解:由于以x轴负方向为电场强度的正方向,在−d∼d区间,场强均为正值,即场强均沿x轴负方向,沿电场方向电势逐渐降低,故沿+x方向,电势逐渐升高,由于φ−x图线的斜率表示场强大小,在O点附近场强最大,φ−x图线斜率最大,故C正确,ABD错误。
故选:C。
φ−x图线的斜率表示场强大小,沿电场方向电势逐渐降低。
本题考查学生对电场基本知识的掌握,解题关键是掌握φ−x图线的斜率表示场强大小,沿电场方向电势逐渐降低。
4.【答案】D
【解析】解:A.卫星绕行星表面运动时速度最大,则GMmR2=mv2R
其中M=43πR3ρ
解得卫星的最大运行速度大小为v= 4ρGπR23,故A正确;
B.卫星的最大加速度大小为a=v2R=4ρGπR3,故B正确;
C.卫星的最大运行角速度为ω=vR= 4πρG3,故C正确;
D.卫星与行星中心连线单位时间内扫过的最大面积为S=12RL=12RvΔt=R2 13πρG(其中△t=1s),故D错误。
本题选择错误的,
故选:D。
卫星绕行星做的是匀速圆周运动,根据行星表面万有引力提供向心力求解第一宇宙速度,即为此卫星的速度.结合轨道半径求出卫星加速度和角速度。
解决本题的关键掌握卫星绕行星运行时,由万有引力提供向心力,运用万有引力定律和圆周运动的规律结合解答.
5.【答案】BC
【解析】解:AB、根据电流间相互作用的规律,可知同向电流相互吸引,反向电流相互排斥,故a、b、c受到的安培力分别如图所示
根据矢量合成法则,可知导线a和导线b受到的安培力方向不同,导线a和导线c受到的安培力方向相反,故A错误,B正确;
C、根据安培定则和矢量合成法则可知,O点磁场的磁感应强度方向垂直bc向下,故C正确;
D、若保持b、c两导线中电流大小不变,方向反向,则O点磁场的磁感应强度变为零,故D错误。
故选:BC。
根据左手定则和安培定则可知,在安培力作用下,同向电流相互吸引,反向电流相互排斥,画出a、b、c受到的安培力的示意图,结合矢量合成法则,分析导线a和导线b受到的安培力以及导线a和导线c受到的安培力的关系;根据安培定则和矢量合成法则可知,分析O点磁感应强度的方向;若保持b、c两导线中电流大小不变,方向反向,同理根据矢量求合判断O点磁感应强度的变化。
本题考查了电流周围的磁场以及电流间的相互作用,熟练掌握矢量的合成。
6.【答案】BCD
【解析】解:A.根据题意在a、b端输入电压的有效U=Um 2=10 2 2V=10V
把电阻R1看作a、b端输入电源的内阻,负载看作变压器原线圈的等效电阻R原=k2R负载
当电阻R1与变压器原线圈等效电阻相等,有最大输出功率,即R1两端电压与输出电压相等UR1=U1=5V
根据理想变压器电压与匝数比关系U1U2=n1n2
代入数据解得U2=2.5V,故A错误;
B.由欧姆定律I1=UR1R1=55A=1A
由原副线圈电流间关系I1I2=n2n1
得I2=2A则R2两端电压为UR2=I2R2=2×1V=2V
则R3=U2−UR2I2=2.5−22Ω=0.25Ω,故B正确;
另解:原线圈的等效内阻R原=k2R负载=4(R3+R4)
当R原=R1时,电源有最大输出功率,代入数据解得R3=0.25Ω
C.输出功率P=U2I2=2.5×2W=5W,故C正确;
D.当变压器原线圈中的电流为I1′=0.5A时,原线圈两端电压U1′=U−I1′R1=10V−0.5×5V=7.5V
变压器原线圈的输入功率P1′=U1′I1′=7.5×0.5W=3.75W
故变压器输出功率P2′=P1′=3.75W
同理,当变压器原线圈中的电流1.5A时,输出功率为P2′′=3.75W,故D正确。
故选:BCD。
A.根据有效值与最大值的关系求a、b端输入电压的有效;把电阻R1看作a、b端输入电源的内阻,负载看作变压器原线圈的等效电阻,当电阻R1与变压器原线圈等效电阻相等,有最大输出功率,得到变压器原线圈输入功率,在根据电压与匝数比的关系求解副线圈两端电压;
B.根据欧姆定律求原线圈中的电流,根据变压器电流与匝数比的关系求副线圈中的电流,根据欧姆定律及串联电阻的电压关系求电阻R3的阻值;
C.根据功率公式求输出功率;
D.根据变压器电流与匝数比的关系求副线圈中的电流;根据欧姆定律及串联电路的电压关系求原线圈两端电压,根据功率公式求原线圈消耗的功率,根据功率关系求变压器的输出功率;
本题是原线圈中含有负载的变压器,把变压器原线圈回路的电阻看作a、b端输入电源的内阻,把变压器副线圈负载电阻等效看作变压器原线圈的电阻,可以使问题简化。
7.【答案】BD
【解析】解:A、第一个L2v时间内,作用在金属线框上的外力与安培力等大反向,在0∼L2v时间内t时刻,作用在金属线框上的安培力大小为:
F安=BIl=BERl=BBlvRl
其中线框的有效切割长度l=vt⋅tan30∘
联立解得:F=F安=B2v3t23R∝t2
作用在金属线框ABC上的外力F的大小与时间的平方成正比,故A错误;
B、第一个L2v时间内,感应电流为:I=ER=BlvR= 3Bv2t3R∝t
感应电流与时间成正比,根据欧姆定律可知,则A、B两端的电压与时间也成正比,故B正确;
C、第二个L2v时间内,金属线框中切割磁感线的有效长度为L2tan30∘= 3L6,为恒定值,则感应电动势、感应电流均恒定,故C错误;
D、第三个L2v时间内是线框的AB边由MN运动到PQ,通过金属线框截面的电荷量为:
q=I−Δt=E−RΔt=ΔΦΔtRΔt=BΔSR
由几何知识得:ΔS=12×( 33L+ 36L)×12L= 38L2
联立求得通过金属线框ABC截面的电荷量为:q= 3BL28R,故D正确。
故选:BD。
作用在金属线框上的外力F与安培力等大反向,确定线框切割磁感线的有效长度,推导安培力,感应电流与时间的关系式;利用平均电流,平均电动势的概念求解通过金属线框截面的电荷量。
本题考查电磁感应现象中力学、电路、通过的电荷量相关知识,基础题目。注意有效切割长度的计算,培养综合分析基本能力。
8.【答案】AD
【解析】解:A.小球C在P点时物块A的速度为零,小球C运动到D点时物块A的速度也为零,该过程中小球C的动能变化量为零,由动能定理知:合外力对物块A做的功为零,故A正确;
B.小球C从P点运动到D点的过程中,物块A的动量变化为零,根据动量定理可知,弹簧的弹力和轻绳的拉力以及物块A的重力对物块A的冲量的和为零,故B错误;
C.小球C运动到Q点时,A回到原来的位置,则弹簧弹性势能不变,设C在Q点的速度为v,则A在Q点的速度为vcosθ,由功能关系有
FL=12⋅12mv2+12m(vcosθ)2(此时物块B对地面的压力恰好为零,速度为零)
代入数据解得v= 100FL43m
则物块A的速度大小为6 FL43m,故C错误;
D.小球C运动到直杆Q点时的速度达到最大,则此时C受合力为零,设绳对小球C的拉力为T,则小球C在Q点,由平衡关系有
Tcosθ=F①
C在Q点时,对物块A,由牛顿第二定律有
|T−mg−F弹|=ma②
F弹=mg③
联立①②③代入数据得A的加速度a=|5F3m−2g|,故D正确。
故选:AD。
由动能定理知,合外力对物体所做的功等于物体动能的变化量。物体所受合外力的冲量等于物体动量的变化量。轻绳对系统整体不做功,由功能关系可求C选项。由牛顿第二定律和对称性可求D选项。
本题的关键在于轻绳对系统不做功、小球C运动到Q点时物块B刚好没有动。
9.【答案】x2−2x1T2 槽码的重力 小车的质量
【解析】解:(1)利用逐差法可知:Δx=aT2
根据图乙数据可知,a=(x2−x1)−x1T2=x2−2x1T2;
(2)设小车的质量为M,槽码的重力为G,如果合外力一定时,加速度与质量成反比,则有:G=(m+M)a
整理得:m=G⋅1a−M,结合图像可知,此时b=M,k=G。
即直线的斜率k等于槽码的重力,在纵轴上的截距绝对值为b,等于小车的质量。
故答案为:(1)x2−2x1T2;(2)槽码的重力、小车的质量。
(1)匀变速直线运动相邻相等的时间内位移之差为定值,即Δx=aT2进行分析,即可求得加速度的数值;
(2)根据实验装置的特点,用整体法根据牛顿第二定律写出钩码质量m与加速度的倒数1a的关系式,结合图象分析截距与斜率的意义。
本题考查了探究物体的加速度与质量的关系实验原理,明确逐差公式求加速的意义,掌握图象法探究物理规律的优势。
10.【答案】V2 右 2.862.55V2 小
【解析】解:(1)电压表V2测V1和电阻并联后的总电压,所以量程为3V的电压表是V2,闭合开关S前,应将滑动变阻器的滑片移到最右端,使回路电流最小,保护电路。
(2)根据闭合电路欧姆定律U2=E−U2−U1R0r
整理得U2=ER0R0+r+rR0+rU1
根据k=rR0+r=0.56,b=ER0R0+r=1.26
解得E=2.86V,r=2.55Ω
(3)公式中代入为R0的电流,实际上由于电压表V2的分流,R0的电流小于干路电流,使测得的电池组的电动势比真实值小。
故答案为:(1)V2;右;(2)2.86;2.55;(3)V2;小。
(1)估算电路的电流,确定电流表的量程,从安全方便的角度选择滑动变阻器;
(2)从安全的角度看,使滑动变阻器连入的电阻最大,写出U−I表达式,根据图象的斜率和纵截距求电源的电动势和内阻;
(3)明确误差来源,明确电压表V2的分流导致出现误差。
本题考查了实物电路图的分析、实验数据处理,对电压表读数时要先确定其量程与分度值,然后根据指针位置读出其示数;知道实验原理与实验数据处理方法可以求出电源电动势与内阻。
11.【答案】解:(1)设物块与长木板相对静止时系统的速度为v。物块与木板组成的系统全过程在水平方向上动量守恒,设向右为正方向,则有:
0=(m+M)v
解得:v=0
由功能关系可知全过程物块减少的重力势能等于系统克服摩擦力做的功,根据图乙可知摩擦力与相对位移成线性关系,可用F的平均值计算系统克服摩擦力做的功,则有:
mgR=F−⋅2L
其中:F−=2N+6N2=4N
解得:R=0.8m
(2)系统水平方向动量守恒,设任意时刻物块与木板的水平速度大小分别为v1、v2,全过程物块与木板的水平位移大小分别为x1、x2,设向右为正方向,则有:
mv1−Mv2=0
可见任意时刻均有:v1v2=Mm=3
可得:x1x2=Mm=3
又有:x1+x2=R=0.8m
解得长木板运动的位移大小为:x2=0.2m
(3)设物块与挡板碰撞后的瞬间,物块与长木板的速度大小分别为v1′、v2′。以向右为正方向,由水平方向动量守恒得:
mv1′−Mv2′=0
由功能关系得:
mgR=F−L+12mv′12+12Mv′22
解得:v1′= 6m/s,v2′= 63m/s
答:(1)圆弧面AB的半径为0.8m;
(2)物块从A点由静止释放到与长木板相对静止于B点,长木板运动的位移大小为0.2m;
(3)物块与挡板碰撞后的瞬间,物块与长木板的速度大小分别为 6m/s, 63m/s。
【解析】(1)物块与木板组成的系统全过程在水平方向上动量守恒,根据图乙可用F的平均值或图像与轴围成的面积来计算系统克服摩擦力做的功,由功能关系求解;
(2)物块与木板组成的系统全过程在水平方向上动量守恒,任意时刻物块与木板的水平速度大小与质量成反比,全过程物块与木板的水平位移大小也与质量成反比,再结合两者位移大小关系求解;
(3)同理,根据水平方向动量守恒和功能关系求解。
本题主要是考查了动量守恒定律和能量守恒定律。对于动量守恒定律,其守恒条件是:系统不受外力作用或某一方向不受外力作用;解答时要首先确定一个正方向,利用碰撞前系统的动量和碰撞后系统的动量相等列方程,再根据能量关系列方程求解。
12.【答案】解:(1)根据电场力公式和牛顿第二定律可知:F1=qE=ma1
根据运动学公式可得:L=12a1t12
粒子在竖直方向做匀加速直线运动,水平方向没有外力作用,可知在水平方向做匀速直线运动可得粒子在区域I花费的时间为:t1=2Lv0
结合上式可得:12×qEm×(2Lv0)2=L
解得:E=mv022qL
(2)粒子在区域I做类平抛运动可知,粒子在原点时速度的方向延长线交水平位移的中点,
可得粒子离开电场区域时的速度与x轴的夹角:α=45∘速度大小v= 2v0
粒子在磁场运动时,洛伦兹力提供向心力,根据牛顿第二定律可得:Bqv=mv2r
解得:r=mvBq而由几何关系有:cos45∘=12Lr
结合上式可得:B=2mv0qL
(3)由题意可知,区域II电场强度变为原来的二倍,故所花费的时间和水平位移为粒子在区域I的一半,分析可知,粒子从x轴上下方经过x轴时距离P点得距离不同,故要分情况讨论:
当n为奇数时,当n=1时,距离P点水平距离为2L,n=3时距离P点水平距离为4L,当n=5时,距离P点水平距离为6L,整理可知n取奇数且当(n≥1)时距离P点水平距离为(n+1)L
当n为偶数时,当n=2时距离P点水平距离为0,当n=4时距离P点水平距离为2L,当n=6时距离P点水平距离为4L,整理可知n取偶数且(n≥2)时距离P点水平距离为(n−2)L分析题意可知: 2v0mBq= 22L
而由上述结论:B=2mv0qL
洛伦兹力提供向心力得:Bqv=m4π2T2r,以及T=Lπv0分析可知:粒子在磁场运动一个周期为Lπ2v0在区域I时间为4Lv0,区域II时间为2Lv0
当n=1时,时间为2Lv0
n=2时,时间为4L+Lπ2v0
当n=3时,时间为4L+Lπ2v0+4Lv0
当n=4时,时间为4L+Lπ2v0+4Lv0+4L+Lπ2v0
整理可得n为偶数时且n≥4,时间为(n2)4L+Lπ2v0+(n2−1)2Lv0,
n为奇数时且n≥3,时间为(n−12)(2Lv0+4L+Lπ2v0)
答:(1)匀强电场区域Ⅰ的电场强度大小为mv022qL;
(2)匀强磁场的磁感应强度的大小为2mv0qL;
(3)n取奇数且当(n≥1)时距离P点水平距离为(n+1)L,n取偶数且(n≥2)时距离P点水平距离为(n−2)L;n为偶数时且n≥4,时间为(n2)4L+Lπ2v0+(n2−1)2Lv0,n为奇数时且n≥3,时间为(n−12)(2Lv0+4L+Lπ2v0)。
【解析】(1)根据牛顿第二定律得出粒子的加速度,结合类平抛规律、运动学公式得出场强的大小;
(2)粒子受到的洛伦兹力提供向心力,结合牛顿第二定律和几何关系得出磁感应强度的大小;
(3)对n的数值进行分类讨论,结合运动学公式得出不同情况下的运动时间。
本题主要考查了带电粒子在磁场中的运动,熟悉粒子的受力分析,结合牛顿第二定律和运动学公式即可完成解答。
13.【答案】ABC
【解析】解:A.晶体分为单晶体和多晶体,都具有固定的熔点,但单晶体有规则的几何外形,而多晶体没有规则的几何外形,故A正确;
B.饱和蒸气压的大小与温度有关,降低温度能够使气体的饱和气压降低,从而使气体液化,故B正确;
C.根据理想气体的状态方程pVT=C可知,一定质量的理想气体等压膨胀过程中温度一定升高,理想气体的内能一定增大,同时气体膨胀对外做功,由热力学第一定律可知,气体一定从外界吸热,故C正确;
D.当两分子间的作用力表现为斥力时,分子间的距离增大,分子力做正功,势能减小,故D错误;
E.一定量的理想气体,如果体积不变,根据pVT=C可知,温度降低,压强减小,根据压强的微观意义可知分子每秒平均碰撞器壁次数将减小,故E错误;
故选:ABC。
根据晶体的特点判断;降低温度能够使气体的饱和气压降低,从而使气体液化;根据热力学第一定律判断;结合分子力的特点与分子力做功判断;根据压强的微观意义判断。
该题考查到的知识点较多,知道晶体的特点,明确饱和气压与温度的关系,明确热力学第一定律中的物理量的正负的意义,知道分子势能变化原因。
14.【答案】解:(1)初始时,根据平衡条件p20=p0+10cmHg=75cmHg+10cmHg=85cmHg
缓慢向下压活塞过程,气柱2发生等温变化,根据玻意耳定律p20L20S=p2L2S
根据几何关系L20=L10+10cm=20cm
L2=L20−5cm=15cm
解得p2=113.33cmHg
故A段水银对左管上封口处玻璃的压强大小p=p2−pA=113.33cmHg−10cmHg=103.33cmHg
(2)稳定后p1=p2=113.33cmHg
对缓慢向下压活塞过程,气柱1发生等温变化,根据玻意耳定律p0L10S=p1L1S
解得L1=6.62cm
故活塞下降的高度h=L10−L1+5cm=10cm−6.62cm+5cm=8.38cm
答:(1)稳定后,A段水银对左管上封口处玻璃的压强大小为103.33cmHg;
(2)此过程中活塞下降的高度为8.38cm。
【解析】(1)初始时,根据平衡条件求出初始时刻的压强,缓慢向下压活塞过程,对气柱2根据玻意耳定律求出末态压强;进而求出A段水银对左管上封口处玻璃的压强;
(2)对缓慢向下压活塞过程,气柱1发生等温变化,根据玻意耳定律求出空气柱的长度,再根据几何关系求出活塞下降的高度。
本题考查液柱类问题,解决本题的关键是准确求出密闭气体的压强。本题难度不大。
15.【答案】ABE
【解析】解:A.依题意,波周期T=2πω=2π5π=0.4s,根据振动方程,t=0.2s时,5πt=π,故0.2s后质点P在平衡位置向上振动,根据“上下坡法”,波沿x轴负方向传播,故A正确;
B.由波形图,该波波长λ=2m,则波速v=λT=20.4m/s=5m/s
故B正确;
C.从图示开始,经过1s,质点P振动2.5个周期,质点P运动路程s=2.5×4A=10×10cm=100cm
故C错误;
D.t=0.4s时刻,质点P仍位于平衡位置,所以位移为零,故D错误;
E.t=0.4s至t=0.6s时间内,质点P从平衡位置沿y轴负方向运动再回到平衡位置,质点P速度先减小后增大,故E正确。
故选:ABE。
A.根据“上下坡法”,波沿x轴负方向传播;
B.根据波形图,确定波长和周期,求波速;
C.一个周期内,质点振动路程为4个振幅;
D.从平衡位置沿y轴负方向运动再回到平衡位置,速度先减小后增大。
本题解题关键是正确使用“上下坡法”,确定波的传播方向,根据波速公式求波速,并掌握一个周期内,质点振动路程为4个振幅。
16.【答案】解:(1)设光线折射到BC边的G点,根据题意画出光路图如下
设AB边的折射角为∠1,根据折射定律有n=sin60∘sin∠1
根据几何关系有14LBG=L2L−BG
联立解得BG=13L,EG=512L,FG=56L
∠1=37∘,n=5 36
因为sinC=1n=2 35
(2)根据折射率与光速的关系有n=cv⇒v=2 35c
光从E点传播到F点所用的时间为t=EG+GFv⇒t=25 324Lc
答:(1)玻璃砖对光的折射率5 36;
(2)光射到BC边时能发生全反射;光从E点传播到F点所用的时间25 324Lc。
【解析】(1)根据题意画出光路图,根据折射定律和几何关系,分析是否发生全发射;
(2)根据折射率与光速的关系,求光的传播时间。
本题解题关键是正确画出光路图,并结合折射定律和全发射条件去分析,是一道中等难度题。
2023年湘豫名校联考高考物理二模试卷-普通用卷: 这是一份2023年湘豫名校联考高考物理二模试卷-普通用卷,共21页。
2023届河南省湘豫名校联考高三上学期12月期末摸底考试物理试卷含解析: 这是一份2023届河南省湘豫名校联考高三上学期12月期末摸底考试物理试卷含解析,共15页。试卷主要包含了 本试卷共8页等内容,欢迎下载使用。
2023届河南省湘豫名校联考高三上学期12月期末摸底考试物理试卷(解析版): 这是一份2023届河南省湘豫名校联考高三上学期12月期末摸底考试物理试卷(解析版),共15页。试卷主要包含了 本试卷共8页等内容,欢迎下载使用。











