









人教B版高二数学选择性必修第三册6.2.2《导数与函数的极值、最值(2)》课件+教案
展开6.2.2 导数与函数的极值、最值 (2)
本节课选自《2019人教B版高中数学选择性必修三》第六章《导数及其应用》,本节课主要学习导数与函数的极值、最值
学生已经具有导数概念、导数几何意义、导数计算、函数的单调性等相关的数学概念知识,对函数的单调性有一定的认识,对相应导数的内容也具有一定的储备。
函数的极值与最值是函数的一个重要性质。在学习运用导数判断函数单调性的基础上,研究和学习函数的极值与最值是导数的一个重要应用,注意培养学生数形结合思想、特殊到一般的研究方法,发展学生直观想象、数学抽象、逻辑推理和数学运算核心素养。
课程目标 | 学科素养 |
A. 理解极值与最值的区别与联系. B.会求函数在闭区间上的最值. C.能利用导数解决与函数最值相关的综合问题.
| 1.数学抽象:求函数最值的方法 2.逻辑推理:函数极值与最值的关系 3.数学运算:运用导数求函数的最值 4.直观想象:最值与极值的关系 |
重点:求函数最值的方法及其综合应用
难点:函数最大(小)值的概念以及与函数极值的区别与联系
多媒体
教学过程 | 教学设计意图 核心素养目标 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
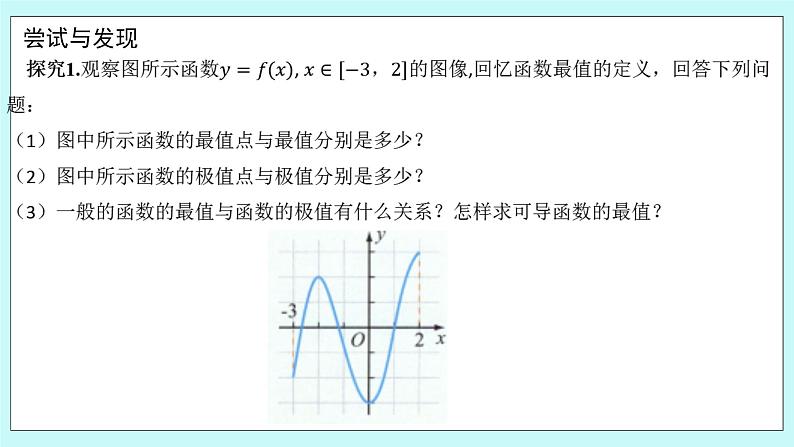
一、 情景导学 探究1.观察图所示函数, 的图像,回忆函数最值的定义,回答下列问题: (1)图中所示函数的最值点与最值分别是多少? (2)图中所示函数的极值点与极值分别是多少? (3)一般的函数的最值与函数的极值有什么关系?怎样求可导函数的最值?
我们知道,函数的最大(小)值是函数定义域内最大(小)的函数值.因此,图所示函数, 的最大值点为2,最大值为3;最小值点为0,最小值为-3.而且,函数的极大值点为-2,极大值为2;极小值点为0,极小值为-3.
1.函数的最值 (1)一般地,如果函数y=f(x)在定义域内的每一点都可导,且函数存在最值,则函数的最值点一定是某个极值点; (2)如果函数y=f(x)的定义域为[a,b] 且存在最值,函数y=f(x)在(a,b)内可导,那么函数的最值点要么是极值点 ,要么是区间端点a或b. 问题1:函数的极值与最值的区别是什么? 函数的最大值和最小值是一个整体性概念,最大(小)值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有多个,但最值只能有一个;极值只能在区间内取得,最值则可以在端点取得;有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点必定是极值.
问题2.求函数f (x)在闭区间[a,b]上的最值的步骤 (1)求函数y=f (x)在区间(a,b)上的极值 ; (2)将函数y=f (x)的各极值与端点处的函数值f (a),f (b)比较,其中最大的一个是最大值,最小的一个是最小值. 1.判断正误(正确的打“√”,错误的打“×”) (1)函数f (x)在区间[a,b]上的最大值和最小值,一定在区间端点处取得.( ) (2)开区间上的单调连续函数无最值. ( ) (3)在定义域内,若函数有最值与极值,则极大(小 值就是最大(小)值. ( ) (4)若函数y=f (x)在区间[a,b]上连续,则一定有最值;若可导,则最值点为极值点或区间端点. ( ) 解析: (1)函数在闭区间[a,b]上的最值可能在端点处取得,也可能在极值点处取得. (2)若单调函数有最值,则一定在区间端点处取得,但开区间上的单调连续函数在端点处无函数值,所以无最值,故正确. (3)因为y最大值≥y极值,y最小值≤y极值,故错误. (4)正确. [答案] (1)× (2)√ (3)× (4)√ 二、典例解析 例3.已知, 求的极值点以及极值,最值点以及最值. 解:当时,
解方程,可得或 解不等式,可得或,此时递增, 解不等式,可得此时递减. 因此, 在上递增,在上递减,在上递增. 由于,从而可知是函数的极大值点,极大值为 ; 是函数的极小值点,极小值为, 又因为 ,所以函数的最大值点为1,最大值为注意到 对任意实数都是成立的,因此可知函数的最小值点为0,而且最小值是 求函数最值的解题策略 (1)如果在区间[a,b]上函数y=f(x)的图像是一条连续不间断的曲线,那么它必有最大值和最小值. (2)如果函数y=f(x)在区间(a,b)内可导,求f(x)在区间[a,b]上的最值可简化过程,即直接将极值点的函数值与端点的函数值比较大小,即可判定最大(或最小)的函数值,就是最大(或最小)值. (3)求函数在闭区间上的最值时,需要对各个极值与端点的函数值进行比较,有时需要作差、作商,有时还要估算,甚至有时需要进行分类讨论. (4)求函数在开区间上的最值时,要借助导数分析研究函数的单调性与极值情况,从而画出函数的大致图像,结合图像求出最值. 跟踪训练1. 求下列函数的最值: (1)f(x)=x3-2x2+1,x∈[-1,2]; (2)f(x)=sin 2x-x,x∈; (3)f(x)=-x. 解:(1)f'(x)=3x2-4x,令f'(x)=0,有3x2-4x=0,解得x=0或x=. 当x变化时,f'(x),f(x)的变化情况如下表:
从上表可知,最大值是f(0)=f(2)=1,最小值是f(-1)=-2. (2)f'(x)=2cos 2x-1,x∈, 令f'(x)=0,得x=-或x=. 当x变化时,f'(x),f(x)的变化情况如下表:
由上表可知, 当x=-时,f(x)取得最大值f, 当x=时,f(x)取得最小值f=-. (3)f(x)的定义域为(0,+∞),f'(x)=-1,令f'(x)=0,得x2=1-ln x,显然x=1是方程的解. 令g(x)=x2+ln x-1,x∈(0,+∞), 则g'(x)=2x+>0, ∴函数g(x)在(0,+∞)上单调递增, ∴x=1是方程f'(x)=0的唯一解. ∵当0<x<1时,f'(x)=-1>0, 当x>1时,f'(x)<0,∴函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减, ∴当x=1时,函数f(x)有最大值,且最大值是f(1)=-1,函数f(x)无最小值. 例4. (1)若函数f(x)=ax3+bx-4在x=1处取得极值,且极值为0,求实数a,b的值; (2)已知函数f(x)=ax3-6ax2+b(a≠0),是否存在实数a,b使f(x)在区间 [-1,2]上取得最大值3,最小值-29?若存在,求出a,b的值;若不存在,请说明理由. 思路分析(1)可利用f'(1)=0,f(1)=0求解; (2)利用求最值的方法建立关于a,b的方程组确定a,b的值,注意对a的讨论. 解:(1)由于f(x)=ax3+bx-4,所以f'(x)=3ax2+b. 依题意,可得f'(1)=0且f(1)=0. 即解得 (2)存在.f'(x)=3ax2-12ax=3ax(x-4), 令f'(x)=0,解得x1=0,x2=4(舍去). ①当a>0,x变化时,f'(x),f(x)的变化情况如下表:
所以当x=0时,f(x)取得最大值.所以b=3. 又f(2)=-16a+3,f(-1)=-7a+3,f(-1)>f(2),所以当x=2时,f(x)取得最小值, 所以-16a+3=-29,即a=2. ②当a<0,x变化时,f'(x),f(x)的变化情况如下表:
所以当x=0时,f(x)取得最小值.所以b=-29. 又f(2)=-16a-29,f(-1)=-7a-29,f(2)>f(-1),所以当x=2时,f(x)取得最大值, 所以-16a-29=3,即a=-2. 综上所述,a=2,b=3或a=-2,b=-29.
跟踪训练2. 已知函数f(x)= x3- (m+3)x2+(m+6)x(x∈R,m为常数),在区间(1,+∞)内有两个极值点,求实数m的取值范围. 解:f'(x)=x2-(m+3)x+m+6. 因为函数f(x)在(1,+∞)内有两个极值点, 所以f'(x)=x2-(m+3)x+m+6在(1,+∞)内与x轴有两个不同的交点, 如图所示.
所以 解得m>3.故实数m的取值范围是(3,+∞).
|
通过具体问题的思考和分析,提出函数最值的概念。发展学生数学抽象和数学建模的核心素养。
由特殊到一般的思想,归纳出导数与函数最值的关系,并帮助学生理解极值与最值的联系与区别,发展学生数学抽象、逻辑推理和数学建模的核心素养。
通过典型例题,加深学生对运用导数求函数最值的方法的理解和运用,发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
三、达标检测 1.函数f(x)=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是( ) A.5,-15 B.5,-4 C.-4,-15 D.5,-16 解析:由f'(x)=6x2-6x-12=6(x+1)(x-2)=0,得x=-1或x=2. 因为f(0)=5,f(2)=-15,f(3)=-4, 所以f(2)<f(3)<f(0), 所以f(x)max=f(0)=5,f(x)min=f(2)=-15. 答案:A 2.函数y=的最大值为( ) A.e-1 B.e C.e2 D.10 A [令y′==0⇒x=e.当x>e时,y′<0; 当0<x<e时,y′>0,所以y极大值=e-1, 因为在定义域内只有一个极值,所以ymax=e-1.] 3.设函数f (x)=x3--2x+5,若对任意x∈[-1,2],都有f (x)>m,则实数m的取值范围是________. [f ′(x)=3x2-x-2=0,x=1或x=-.f (-1)=,f =,f (1)=,f (2)=7,∴m<.] 4.已知函数f(x)=2x3-6x2+m(m∈R)在区间[-2,2]上有最大值3,求它在[-2,2]上的最小值. 解:f'(x)=6x2-12x=6x(x-2), 在(-2,2)上,只有x=0是f(x)的极值点,且为极大值点, ∴f(x)极大值=f(0)=m. 又f(-2)=-16-24+m=m-40, f(2)=16-24+m=m-8. 容易判断m-40<m-8<m,∴m=3, ∴f(x)min=m-40=-37,即最小值是-37. 5.已知a是实数,函数f (x)=x2(x-a),求f (x)在区间[0,2]上的最大值. [解] f ′(x)=3x2-2ax. 令f ′(x)=0,解得x1=0,x2=. ①当≤0,即a≤0时, f (x)在[0,2]上单调递增,从而f (x)max=f (2)=8-4a. ②当≥2,即a≥3时,f (x)在[0,2]上单调递减,从而f (x)max=f (0)=0. ③当0<<2,即0<a<3时,f (x)在上单调递减,在上单调递增, 从而f (x)max= 综上所述,f (x)max= |
通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
四、小结 求f(x)在[a,b]上的最大值与最小值的步骤如下: (1)f(x)在(a,b)内导函数为零的点,并计算出其函数值; (2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
五、课时练 | 通过总结,让学生进一步巩固本节所学内容,提高概括能力。 |
由于教师不仅是知识的传授者,而且也是学生学习的引导者、组织者和合作者。所以我采用“问题情景---建立模型---求解---解释---应用”的教学模式,启发引导学生通过对问题的亲身动手探求、体验,获得不仅是知识,更重要的是掌握了在今后的发展中用这种手段去获取更多的知识的方法。这是“教师教给学生寻找水的方法或给学生一杯水,使学生能找到一桶水乃至更多活水”的求知方式。多媒体可以使教学内容生动、形象、鲜明地得到展示。









