高中数学1.2.4 二面角优质ppt课件

课程目标

学科素养

A.掌握二面角的概念.

B.理解二面角的平面角的含义.

C.会用向量法解决二面角的计算问题.

1.数学抽象：二面角的定义

2.逻辑推理：二面角的定义

3.直观想象：二面角的几何模型

4.数学运算：用向量法解决二面角的计算问题

教学过程

教学设计意图

核心素养目标

一、情境导学

问题1：日常生活中，很多场景中都有平面与平面呈一定角度的形象，例如如图（1）所示，在建造大坝时为了加固大坝大巴外侧的平面，一般于水平面呈一定角度，如图（2）所示，很多屋顶都是二面角的形象，
你能找到日常生活中更多类似的例子吗？怎样刻画平面与平面所成的角呢？

1.二面角及其度量

1.在正方体ABCD-A1B1C1D1中,平面B1C1DA与平面BCDA所成二面角的大小为　　　　. 

答案:45°

2.两个平面相交时,它们所成角的取值范围是什么?

提示:(0°,90°]

问题2：如图所示，设为二面角的半平面上一点，过点做半平面的垂线，设O为棱上一点

（1）判断是什么条件；

（2）由二面角的作法，你能得到什么启发？

提示：（1）充要条件
（2）若二面角的大小为

=

问题3：如果, 分别是平面, 的一个法向量,设所成角的大小为，通过作图讨论与<, >的关系.

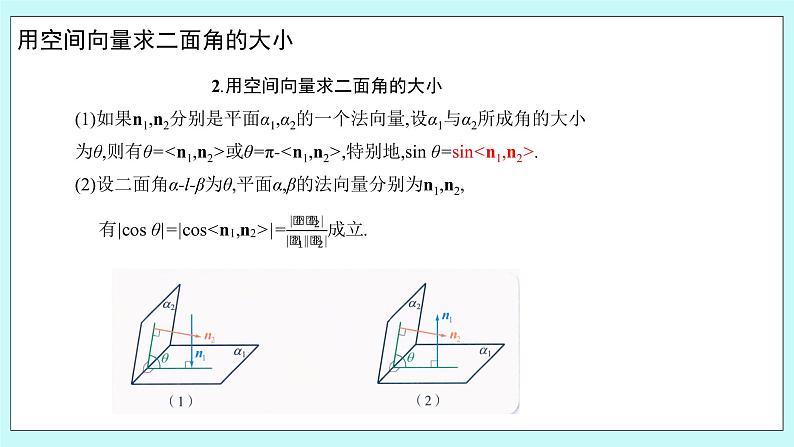
2.用空间向量求二面角的大小

(1)如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,则有θ=<n1,n2>或θ=π-<n1,n2>,特别地,sin θ=sin<n1,n2>.

(2)设二面角α-l-β为θ,平面α,β的法向量分别为n1,n2,

有|cos θ|=|cos<n1,n2>|=成立.

点睛： 利用公式cos<n1,n2>=(n1,n2分别为两平面的法向量)进行求解,注意<n1,n2>与二面角大小的关系,是相等还是互补,需结合图形进行判断.

如图(2)(4)中<n1,n2>就是二面角α-l-β的平面角的补角;如图(1)(3)中<n1,n2>就是二面角α-l-β的平面角.

3.判断

(1)二面角的大小就是该二面角两个半平面的法向量的夹角.(　　)

(2)若二面角两个半平面的法向量的夹角为120°,则该二面角的大小等于60°或120°.(　　)

答案:(1)×　(2)√

4.在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的角的余弦值为(　　)

A.　　　B.　　　C.　　　D.

解：以A为原点建立如图所示的空间直角坐标系Axyz,设棱长为1,

则A1(0,0,1),E,D(0,1,0),∴=(0,1,-1),,

设平面A1ED的一个法向量为n1=(x,y,z),

则令x=1,则y=2,z=2,  ∴n1=(1,2,2).

∵平面ABCD的一个法向量为n2=(0,0,1),

∴cos<n1,n2>=,

即平面A1ED与平面ABCD所成角的余弦值为.

答案:B

二、典例解析

例1 如图所示,PC⊥平面ABC,AB=BC=CA=PC,求二面角B-PA-C的平面角的正切值.

分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射影在AC上,由此可用三垂线定理作出二面角的平面角.

解:∵PC⊥平面ABC,∴平面PAC⊥平面ABC,交线为AC.作BD⊥AC于D点,据面面垂直性质定理,BD⊥平面PAC,作DE⊥PA于E点,连接BE,据三垂线定理,则BE⊥PA,从而∠BED是二面角B-PA-C的平面角.

设PC=a,依题意知△ABC是边长为a的正三角形,

∴D是AC的中点,且BD=a.

∵PC=CA=a,∠PCA=90°,∴∠PAC=45°,

∴在Rt△DEA中,ED=AD·sin 45°=a,

则在Rt△BED中,tan∠BED=.

故二面角B-PA-C的平面角的正切值为.

1.本题解法使用了三垂线定理来作出二面角的平面角后,再用解三角形的方法来求解.

2.二面角的定义求法主要有:

(1)由定义作出二面角的平面角;

(2)利用三垂线定理(逆定理)作出二面角的平面角;

(3)作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是二面角的平面角.

跟踪训练1 如图,已知二面角α-a-β等于120°,PA⊥α,A∈α,PB⊥β,B∈β,求∠APB的大小.

解:设平面PAOB∩α=OA,平面PAOB∩β=OB.

∵PA⊥α,a⊂α,∴PA⊥a.同理PB⊥a.∴a⊥平面PAOB.

又∵OA⊂平面PAOB,∴a⊥OA.同理a⊥OB.

∴∠AOB是二面角α-a-β的平面角.

在四边形PAOB中,∠AOB=120°,

∠PAO=∠PBO=90°,所以∠APB=60°.

例2：如图所示，已知直三棱柱中,

, =2,且D是的中点.求平面BDC与平面BD所成角的大小.

解:以题意，

以C为原点, ，，的方向分别为轴正方向，

建立如图所示直角坐标系，

则： C

所以=(0,1,0), =(1,0,1) , =(-1,0,1) , =(0,-1,2) ,

设平面的一个法向量为,

则

取=1，可得 ,此时,

设平面的一个法向量为m,

则

取=1，可得 ,此时m,

因为0，所以=

从而可知平面BDC与平面BD所成角的大小为，

也就是说，这两个平面是相互垂直的。

        利用向量方法求二面角的大小时,多采用求法向量的方法,即求出两个面的法向量,然后通过法向量的夹角来得到二面角的大小,但利用这种方法求解时,要注意结合图形观察分析,确定二面角是锐二面角还是钝二面角,不能将两个法向量的夹角与二面角的大小完全等同起来.

跟踪训练2  如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.

(1)证明:O1O⊥底面ABCD;

(2)若∠CBA=60°,求二面角C1-OB1-D的余弦值.

(1)证明:因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,

又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,

因为AC∩BD=O,所以O1O⊥底面ABCD.

(2)解:因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD,又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.

如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系. 设棱长为2,因为∠CBA=60°,

所以OB=  ,OC=1,  所以O(0,0,0),B1(,0,2),C1(0,1,2),

平面CB1D的一个法向量为n=(0,1,0),

设平面OC1B1的法向量为m=(x,y,z),则=(,0,2),=(0,1,2),

则由m⊥,m⊥,得x+2z=0,y+2z=0,

取z=-,则x=2,y=2,所以m=(2,2,-),

所以cos<m,n>=.

由图形可知二面角C1-OB1-D的大小为锐角,所以二面角C1-OB1-D的余弦值为.

探究变式 如果本例条件不变,求二面角B-A1C-D的余弦值.

解:由例2(2)知B(,0,0),A1(0,-1,2),C(0,1,0),D(-,0,0),

设平面BA1C的法向量为m=(x1,y1,z1),

=(0,2,-2),=(-,1,0),

则

令x1=1,则y1=,z1=,

∴m=(1,),

同理得,平面A1CD的法向量n=(1,-,-),

cos<m,n>==-,由图可知二面角B-A1C-D的大小为钝角,

则二面角B-A1C-D的余弦值为-.

通过来源于生活中的面与面所成角的问题，帮助学生发现问题，并建立二面角的概念，提升学生数学抽象，逻辑推理和数学建模的核心素养。

通过梳理求解二面角的基本方法和步骤，提升运算速度和准确度，让学生感受，用代数方法解问题决立体几何问题。发展学生逻辑推理，数学抽象和数学运算的核心素养。

通过典例解析想，对二面角典型问题的分析解决，明确思考方向，让学生感受，用代数方法解问题决立体几何问题。发展学生逻辑推理，数学抽象和数学运算的核心素养。

通过典型例题的分析和解决，让学生感受空间向量坐标运算在解决空间几何中的应用。发展学生数学抽象、逻辑推理的核心素养。

三、达标检测

1.已知平面α内有一个以AB为直径的圆,PA⊥α,点C在圆周上(异于点A,B),点D,E分别是点A在PC,PB上的射影,则(　　)

A.∠ADE是二面角A-PC-B的平面角

B.∠AED是二面角A-PB-C的平面角

C.∠DAE是二面角B-PA-C的平面角

D.∠ACB是二面角A-PC-B的平面角

答案:B

2.已知二面角α-l-β的两个半平面α与β的法向量分别为a,b,若<a,b>=,则二面角α-l-β的大小为(　　)

A. B.          C.    D.

解析:由于二面角的范围是[0,π],而二面角的两个半平面α与β的法向量都有两个方向,因此二面角α-l-β的大小为,故选C.

答案:C

3.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为(　　)

 A.45° B.135°     C.45°或135°         D.90°

解析:cos<m,n>=,即<m,n>=45°.所以两平面所成二面角为45°或180°-45°=135°.

答案:C

4.如图所示,点A,B,C分别在空间直角坐标系Oxyz的三条坐标轴上,=(0,0,2),平面ABC的一个法向量为n=(2,1,2),设二面角C-AB-O的大小为θ,则cos θ=　　　　. 

解析:cos θ=.

答案:

5.如图所示,在几何体S-ABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,求平面SAD与平面SAB所成角的余弦值.

解:如图,过点D作DC的垂线交SC于E,以D为原点,以DC,DE,DA所在直线分别为x,y,z轴建立空间直角坐标系.

∵∠SDC=120°,∴∠SDE=30°,又SD=2,∴点S到y轴的距离为1,

到x轴的距离为,则有D(0,0,0),S(-1,,0),A(0,0,2),C(2,0,0),B(2,0,1),设平面SAD的法向量为m=(x,y,z),

∵=(0,0,-2),=(-1,,-2),

∴

取x=,得平面SAD的一个法向量为m=(,1,0).

又=(2,0,-1),设平面SAB的法向量为n=(a,b,c),

则令a=,

则n=(,5,2),

∴cos<m,n>=,

故平面SAD与平面SAB所成角的余弦值是.

通过练习巩固本节所学知识，通过学生解决问题，发展学生的数学运算、逻辑推理、数学建模的核心素养。

四、小结

五、课时练

通过总结，让学生进一步巩固本节所学内容，提高概括能力。