人教B版 (2019)选择性必修 第一册2.7.2 抛物线的几何性质完美版ppt课件

课程目标

学科素养

A.掌握抛物线的简单几何性质.

B.了解抛物线几何性质的简单应用.

C.能利用方程及数形结合思想解决焦点弦、弦中点等问题.

1.数学抽象：抛物线的几何性质

2.逻辑推理：直线与抛物线的位置关系

3.数学运算：运用方程解决直线与抛物线有关弦的问题

4.直观想象：抛物线几何性质的简单应用

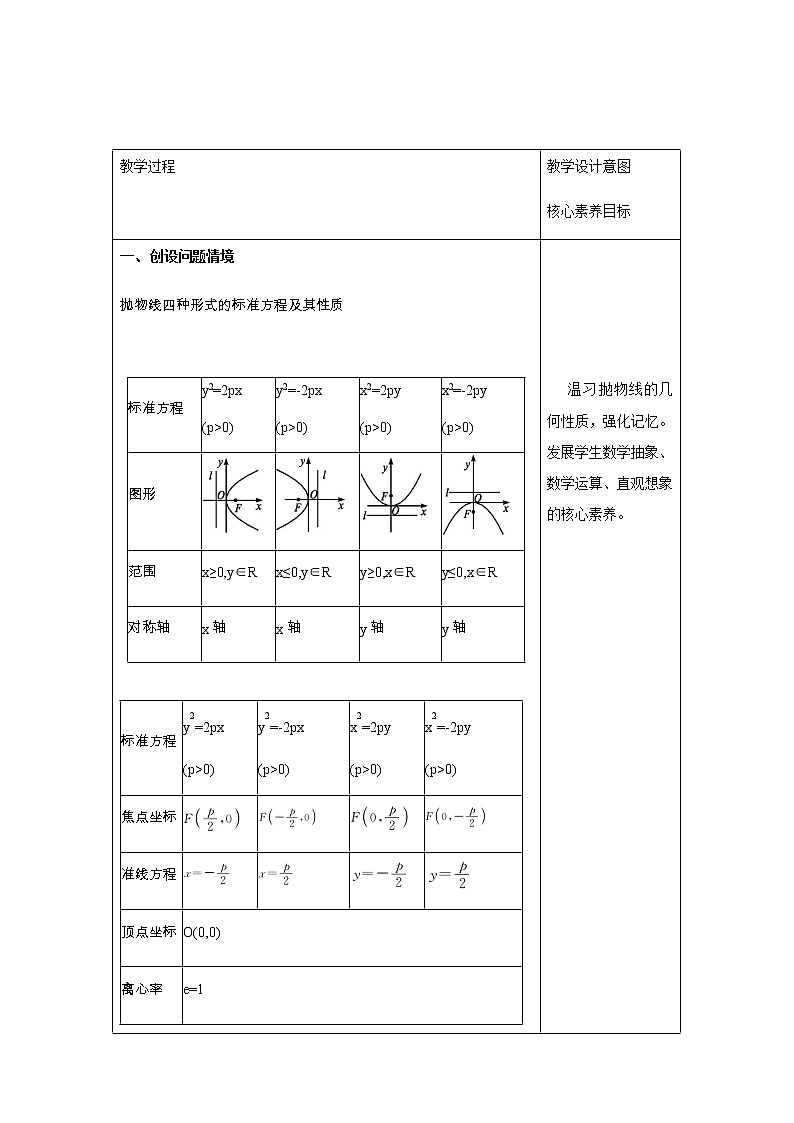
教学过程

教学设计意图

核心素养目标

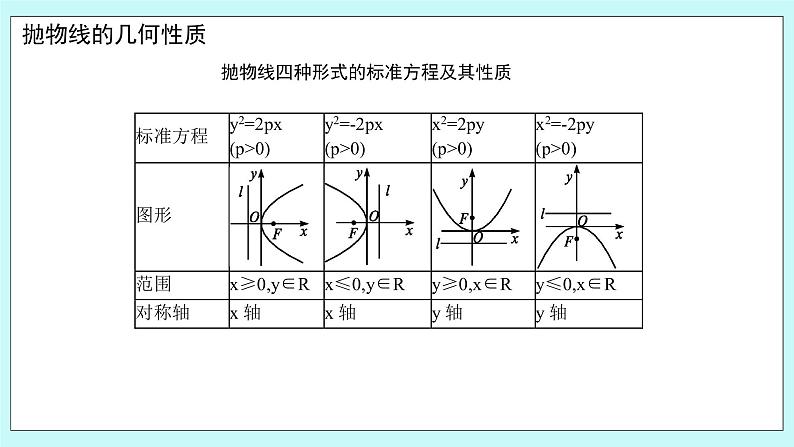
一、    创设问题情境

抛物线四种形式的标准方程及其性质

1.对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,

其共同点:(1)顶点都为原点;

(2)对称轴为坐标轴;

(3)准线与对称轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的 ;

(4)焦点到准线的距离均为p.

其不同点:(1)对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2;(2)开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程的右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.

2.只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程.

二、典例解析

例1(1)等腰直角三角形AOB内接于抛物线y2=2px(p>0),O为抛物线的顶点,OA⊥OB,则△AOB的面积是(　　)

A.8p2      B.4p2      C.2p2             D.p2

(2)如图所示,F是抛物线y2=4x的焦点,点A,B分别在抛物线y2=4x及圆x2+y2-2x-3=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是(　　)

A.(4,6)  B.[4,6]       C.(2,4)     D.[2,4]

解析:(1)因为抛物线的对称轴为x轴,内接△AOB为等腰直角三角形,所以由抛物线的对称性知,直线AB与抛物线的对称轴垂直,从而直线OA与x轴的夹角为45°.

由方程组

所以A,B两点的坐标分别为(2p,2p)和(2p,-2p).

所以|AB|=4p,所以S△AOB=×4p×2p=4p2.

(2)由题意知抛物线y2=4x的准线为x=-1,

由消去y整理得x2+2x-3=0,解得x=1,

设A,B两点的坐标分别为A(x1,y0),B(x2,y0),则|AF|=x1+1.

∵B在图中圆(x-1)2+y2=4的实线部分上运动,

∴1<x2<3.∴△FAB的周长为|AF|+|FB|+|BA|=(x1+1)+2+(x2-x1)=x2+3∈(4,6).

答案:(1)B　(2)A

(3)已知抛物线的顶点在坐标原点,对称轴为x轴,且与圆x2+y2=4相交于A,B两点,|AB|=2

,求抛物线方程.

解:由已知,抛物线的焦点可能在x轴正半轴上,也可能在负半轴上.

故可设抛物线方程为y2=ax(a≠0).

设抛物线与圆x2+y2=4的交点A(x1,y1),B(x2,y2).

∵抛物线y2=ax(a≠0)与圆x2+y2=4都关于x轴对称,

∴A与B关于x轴对称,

∴|y1|=|y2|且|y1|+|y2|=2,

∴|y1|=|y2|=,代入圆x2+y2=4,

得x2+3=4,∴x=±1,

∴A(±1,)或A(±1,-),代入抛物线方程,

得a=±3.∴所求抛物线方程是y2=3x或y2=-3x.

研究抛物线的几何性质要从三个方面入手

(1)开口:由抛物线的标准方程看图像开口,关键是看准二次项是x还是y,一次项的系数是正还是负.

(2)关系:顶点位于焦点与准线中间,准线垂直于对称轴.

(3)定值:焦点到准线的距离为p;过焦点垂直于对称轴的弦(又称为通径)长为2p;离心率恒等于1.

跟踪训练1 已知抛物线y2=8x.

(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;

(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,

若焦点F是△OAB的重心,求△OAB的周长.

解:(1)抛物线y2=8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.

(2)如图所示,由|OA|=|OB|可知AB⊥x轴,垂足为点M,

又焦点F是△OAB的重心,

则|OF|=|OM|. 因为F(2,0),

所以|OM|=|OF|=3,所以M(3,0).故设A(3,m),

代入y2=8x得m2=24,

所以m=2或m=-2,

所以A(3,2),B(3,-2),

所以|OA|=|OB|=,

所以△OAB的周长为2+4.

例2 (1)对于抛物线C:y2=4x,我们称满足 <4x0的点M(x0,y0)在抛物线的内部.若点M(x0,y0)在抛物线内部,则直线l:y0y=2(x+x0)与曲线C(　　)

A.恰有一个公共点          B.恰有2个公共点

C.可能有一个公共点,也可能有两个公共点

D.没有公共点

解析:由y2=4x与y0y=2(x+x0)联立,消去x,得y2-2y0y+4x0=0,

∴Δ=4-4×4x0=4(-4x0).

∵<4x0,∴Δ<0,直线和抛物线无公共点.

答案:D

(2)已知抛物线方程为y2=2px(p>0),过此抛物线的焦点的直线与抛物线交于A,B两点,且|AB|=p,求直线AB的方程.

解:由题意知焦点F,设A(x1,y1),B(x2,y2),若AB⊥x轴,则|AB|=2p≠p,不满足题意.所以直线AB的斜率存在,设为k,

则直线AB的方程为y=k,k≠0.由消去x,

整理得ky2-2py-kp2=0.由根与系数的关系得y1+y2=,y1y2=-p2.

所以|AB|===2pp,解得k=±2.所以直线AB的方程为2x-y-p=0或2x+y-p=0.

变式 若例2(2)条件不变,求弦AB的中点M到y轴的距离.

解:如图,过A,B,M分别作准线x=-的垂线交准线于C,D,E点.

由定义知|AC|+|BD|=p,则梯形ABDC的中位线|ME|=p,∴M点到y轴的距离为p-p.

1.直线与抛物线位置关系的判断方法

设直线l:y=kx+b,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立消元得k2x2+(2kb-2p)x+b2=0.

(1)若k2=0,此时直线与抛物线有一个交点,该直线平行于抛物线的对称轴或与对称轴重合.

(2)若k2≠0,当Δ>0时,直线与抛物线相交,有两个交点;

当Δ=0时,直线与抛物线相切,有一个交点;

当Δ<0时,直线与抛物线相离,无公共点.

2.求抛物线弦长问题的方法

(1)一般弦长公式

(2)焦点弦长

设过抛物线y2=2px(p>0)的焦点的弦的端点为A(x1,y1),B(x2,y2),则|AB|=x1+x2+p,然后利用弦所在直线方程与抛物线方程联立、消元,由根与系数的关系求出x1+x2即可.

(3)解决焦点弦问题时,应注意焦点弦的几何性质.凡涉及抛物线的弦长、弦的中点、弦的斜率等问题,注意利用根与系数的关系,设而不求,能避免繁杂的计算.

|AB|=|x1-x2|=|y1-y2|.

跟踪训练2 (1)过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2).当PA与PB的斜率存在且倾斜角互补时, 的值为(　　)

A.            B.-2             C.2        D.无法确定

解析:由=2px1,=2px0,得kPA=,

kPB=(x1≠x0,x2≠x0),由PA,PB倾斜角互补知kPA=-kPB,

即=0,可得y1+y2=-2y0,故=-2.

答案:B

(2)已知直线l:y=kx+1,抛物线C:y2=4x.当k为何值时,l与C只有一个公共点;有两个公共点;没有公共点.

解:联立得k2x2+(2k-4)x+1=0.①

当k=0时,①式只有一个解x=,∴y=1,

∴直线l与C只有一个公共点,

此时直线l平行于x轴.

当k≠0时,①式是一个一元二次方程,

Δ=(2k-4)2-4k2=16(1-k).

(ⅰ)当Δ>0,即k<1,且k≠0时,

l与C有两个公共点,此时直线l与C相交;

(ⅱ)当Δ=0,即k=1时,l与C有一个公共点,此时直线l与C相切;

(ⅲ)当Δ<0,即k>1时,l与C没有公共点,此时直线l与C相离.

综上所述,当k=1或0时,l与C有一个公共点;

当k<1且k≠0时,l与C有两个公共点;

当k>1时,l与C没有公共点.

温习抛物线的几何性质，强化记忆。发展学生数学抽象、数学运算、直观想象的核心素养。

通过抛物线几何性质的应用，进一步体会数形结合的思想方法。发展学生数学运算，数学抽象和数学建模的核心素养。

通过典型例题，掌握直线与抛物线的有关问题，提升学生数学建模，数形结合，及方程思想，发展学生逻辑推理，直观想象、数学抽象和数学运算的核心素养。

三、达标检测

1．若抛物线y2＝2x上有两点A，B且AB垂直于x轴，若|AB|＝2，则抛物线的焦点到直线AB的距离为(　　)

A．            B．          C．          D．

【答案】A　[线段AB所在的直线的方程为x＝1，抛物线的焦点坐标为，则焦点到直线AB的距离为1－＝.]

2．已知AB是过抛物线2x2＝y的焦点的弦，若|AB|＝4，则AB的中点的纵坐标是________．

【答案】　[设A(x1，y1)，B(x2，y2)，由抛物线2x2＝y，可得p＝，

∵|AB|＝y1＋y2＋p＝4，∴y1＋y2＝4－＝，

故AB的中点的纵坐标是＝.]

3．若直线x－y＝2与抛物线y2＝4x交于A，B两点，则线段AB的中点坐标是________.

【答案】(4,2)　[由得x2－8x＋4＝0，

设A(x1，y1)，B(x2，y2)，则x1＋x2＝8，y1＋y2＝x1＋x2－4＝4，

故线段AB的中点坐标为(4,2)．]

4．设直线y＝2x＋b与抛物线y2＝4x交于A，B两点，已知弦AB的长为3，求b的值．

【答案】由

消去y，得4x2＋4(b－1)x＋b2＝0.

由Δ＞0，得b＜.设A(x1，y1)，B(x2，y2)．

则x1＋x2＝1－b，x1x2＝.

∴|x1－x2|＝＝.

∴|AB|＝|x1－x2|＝·＝3，∴1－2b＝9，即b＝－4.

5.已知y=x+m与抛物线y2=8x交于A,B两点.

(1)若|AB|=10,求实数m的值;

(2)若OA⊥OB,求实数m的值.

解:由得x2+(2m-8)x+m2=0.

由Δ=(2m-8)2-4m2=64-32m>0,得m<2.

设A(x1,y1),B(x2,y2),

则x1+x2=8-2m,x1x2=m2,y1y2=m(x1+x2)+x1x2+m2=8m.

(1)因为|AB|=

==10,

所以m=,经检验符合题意.

(2)因为OA⊥OB,所以x1x2+y1y2=m2+8m=0,

解得m=-8或m=0(舍去).

所以m=-8,经检验符合题意.

通过练习巩固本节所学知识，通过学生解决问题，发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。

四、小结

五、课时练

通过总结，让学生进一步巩固本节所学内容，提高概括能力。