









高中数学3.3 二项式定理与杨辉三角多媒体教学课件ppt
展开www.ks5u.com3.2 数学探究活动:生日悖论的解释与模拟(略)
3.3 二项式定理与杨辉三角
第1课时 二项式定理
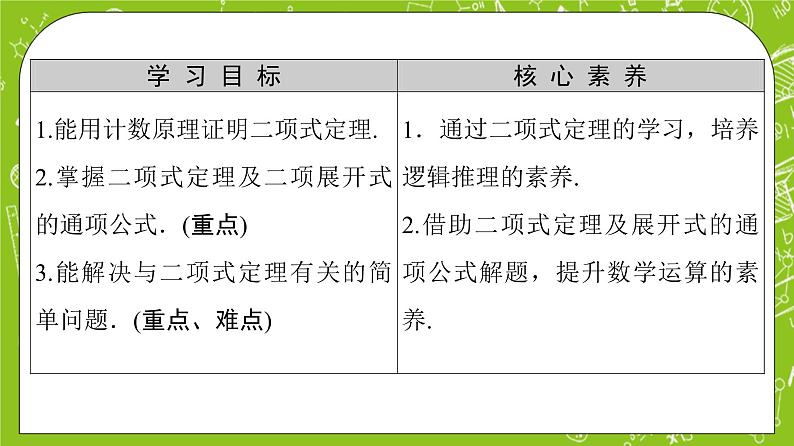
学 习 目 标 | 核 心 素 养 |
1.能用计数原理证明二项式定理. 2.掌握二项式定理及二项展开式的通项公式.(重点) 3.能解决与二项式定理有关的简单问题.(重点、难点) | 1.通过二项式定理的学习,培养逻辑推理的素养. 2.借助二项式定理及展开式的通项公式解题,提升数学运算的素养. |
三个箱子均装着标有a,b字母的两个大小,形状一样的球,从每个箱子摸出一个球,共摸出3个球,有哪些可能结果?每一种结果有多少种情形?
问题:类比上述结果你能联想出(a+b)3展开式的形式吗?
二项式定理及相关的概念
二项式定理 | |
概念 | 公式(a+b)n=Can+Can-1b+Can-2b2+…+Can-rbr+…+Cbn(n∈N+)称为二项式定理 |
二项式系数 | 各项系数C(r=0,1,2,…,n)叫做展开式的二项式系数 |
二项式通项 | Can-rbr是展开式中的第r+1项,可记做Tr+1=Can-rbr(其中0≤r≤n,r∈N,n∈N+) |
二项展开式 | Can+Can-1b+Can-2b2+…+Can-rbr+…+Cbn(n∈N+) |
思考1:二项式定理中,项的系数与二项式系数相同吗?
[提示] 二项式系数与项的系数是完全不同的两个概念.
二项式系数是指C,C,…,C,而项的系数是指该项中除了变量外的常数部分,它不仅与各项的项数有关,而且也与a,b的值有关.
思考2:二项式(a+b)n与(b+a)n展开式的第k+1项是否相同?
[提示] 不同.(a+b)n展开式中第k+1项为Can-kbk,而(b+a)n展开式中第k+1项为Cbn-kak.
1.思考辨析(正确的打“√”,错误的打“×”)
(1)(a+b)n展开式中共有n项. ( )
(2)在公式中,交换a,b的顺序对各项没有影响. ( )
(3)Can-rbr是(a+b)n展开式中的第r项. ( )
(4)(a-b)n与(a+b)n的二项式展开式的二项式系数相同. ( )
[答案] (1)× (2)× (3)× (4)√
2.(x+1)n的展开式共11项,则n等于( )
A.9 B.10
C.11 D.12
B [由n+1=11,可知n=10.]
3.(y-2x)8展开式中的第6项的二项式系数是( )
A.C B.C(-2)5
C.C D.C(-2)6
C [由题意可知第6项的二项式系数为C.]
4.(x+2)6的展开式中x3的系数是________.
160 [法一:设含x3的项为第r+1项,则Tr+1=Cx6-r2r,令6-r=3,则r=3.
故x3的系数为C·23=160.
法二:(x+2)6表示6个括号相乘,要得到含x3的项,只需选出3个括号出x,另三个括号出2即可,即C·x3·23=160x3.]
二项式定理的正用、逆用 |
【例1】 (1)用二项式定理展开;
(2)化简:C(x+1)n-C(x+1)n-1+C(x+1)n-2-…+(-1)rC(x+1)n-r+…+(-1)nC.
[思路点拨] (1)二项式的指数为5,且为两项的和,可直接按二项式定理展开;(2)可先把x+1看成一个整体,分析结构形式,逆用二项式定理求解.
[解] (1)=C(2x)5+C(2x)4·+…+C
=32x5-120x2+-+-.
(2)原式=C(x+1)n+C(x+1)n-1(-1)+C(x+1)n-2·(-1)2+…+C(x+1)n-r(-1)r+…+C(-1)n=[(x+1)+(-1)]n=xn.
1.展开二项式可以按照二项式定理进行.展开时注意二项式定理的结构特征,准确理解二项式的特点是展开二项式的前提条件.
2.对较复杂的二项式,有时先化简再展开会更简便.
3.对于化简多个式子的和时,可以考虑二项式定理的逆用.对于这类问题的求解,要熟悉公式的特点,项数,各项幂指数的规律以及各项的系数.
1.(1)求的展开式;
(2)化简:1+2C+4C+…+2nC.
[解] (1)法一:=C(3)4+C(3)3
·+C(3)2·+C(3)+C
=81x2+108x+54++.
法二:=
=(81x4+108x3+54x2+12x+1)
=81x2+108x+54++.
(2)原式=1+2C+22C+…+2nC=(1+2)n=3n.
二项式系数与项的系数问题 |
【例2】 (1)求二项式的展开式中第6项的二项式系数和第6项的系数;
(2)(教材P33习题33AT2改编)求的展开式中x3的系数.
[思路点拨] 利用二项式定理求展开式中的某一项,可以通过二项展开式的通项公式进行求解.
[解] (1)由已知得二项展开式的通项为Tr+1
=C(2)6-r·
=(-1)rC·26-r·x,
∴T6=-12x.
∴第6项的二项式系数为C=6,
第6项的系数为C·(-1)·2=-12.
(2)Tr+1=Cx9-r·=(-1)r·C·x9-2r,
令9-2r=3,∴r=3,即展开式中第四项含x3,其系数为(-1)3·C=-84.
1.二项式系数都是组合数C(r=0,1,2,…,n),它与二项展开式中某一项的系数不一定相等,要注意区分“二项式系数”与二项式展开式中“项的系数”这两个概念.
2.第r+1项的系数是此项字母前的数连同符号,而此项的二项式系数为C.例如,在(1+2x)7的展开式中,第四项是T4=C17-3(2x)3,其二项式系数是C=35,而第四项的系数是C23=280.
2.求的展开式的第三项的系数和常数项.
[解] T3=C(x3)3=C·x5,所以第三项的系数为C·=.
通项Tr+1=C(x3)5-r=·Cx15-5r,令15-5r=0,得r=3,所以常数项为T4=C(x3)2=.
求展开式中的特定项 |
[探究问题]
1.如何求展开式中的常数项?
[提示] 利用二项展开式的通项Cx4-r·=Cx4-2r求解,令4-2r=0,则r=2,所以展开式中的常数项为C==6.
2.(a+b)(c+d)展开式中的每一项是如何得到的?
[提示] (a+b)(c+d)展开式中的各项都是由a+b中的每一项分别乘以c+d中的每一项再把积相加而得到.
3.如何求(2x+1)3展开式中含x的项?
[提示] (2x+1)3展开式中含x的项是由x+中的x与分别与(2x+1)3展开式中常数项C=1及x2项C22x2=12x2分别相乘再把积相加得x·C+·C(2x)2=x+12x=13x.即(2x+1)3展开式中含x的项为13x.
【例3】 已知在的展开式中,第6项为常数项.
(1)求n;
(2)求含x2项的系数;
(3)求展开式中所有的有理项.
[思路点拨] →
→→→
→→
→
[解] 通项公式为:
Tr+1=Cx(-3)rx=C(-3)rx.
(1)∵第6项为常数项,
∴r=5时,有=0,即n=10.
(2)令=2,得r=(10-6)=2,
∴所求的系数为C(-3)2=405.
(3)由题意得,
令=k(k∈Z),
则10-2r=3k,即r=5-k.
∵r∈Z,∴k应为偶数,
k=2,0,-2,即r=2,5,8,
所以第3项,第6项与第9项为有理项,
它们分别为405x2,-61 236,295 245x-2.
1.求二项展开式的特定项的常见题型
(1)求第k项,Tr=Can-r+1br-1;
(2)求含xr的项(或xpyq的项);
(3)求常数项;
(4)求有理项.
2.求二项展开式的特定项的常用方法
(1)对于常数项,隐含条件是字母的指数为0(即0次项);
(2)对于有理项,一般是先写出通项公式,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解;
(3)对于二项展开式中的整式项,其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.
3.(1)在(1-x3)(1+x)10的展开式中,x5的系数是________.
(2)若展开式的常数项为60,则常数a的值为________.
(1)207 (2)4 [(1)x5应是(1+x)10中含x5项、
含x2项分别与1,-x3相乘的结果,
∴其系数为C+C(-1)=207.
(2)的展开式的通项是
Tr+1=Cx6-r·(-)rx-2r=Cx6-3r(-)r,
令6-3r=0,得r=2,即当r=2时,
Tr+1为常数项,即常数项是Ca,
根据已知得Ca=60,解得a=4.]
1.二项式系数与项的系数是两个不同的概念,前者仅指C,C,…,C,…,而后者指的是除字母以外的所有系数(包括符号).
2.要牢记Can-kbk是展开式的第k+1项,而非第k项.
3.对于非二项式展开式的求解可借助二项式定理的原理求解.
1.在(x-)10的展开式中,含x6的项的系数是( )
A.-27C B.27C
C.-9C D.9C
D [含x6的项是T5=Cx6(-)4=9Cx6.]
2.在的展开式中常数项是( )
A.-28 B.-7
C.7 D.28
C [Tr+1=C··=(-1)r·C··x,当8-r=0,即r=6时,T7=(-1)6·C·=7.]
3.(1-x)10的展开式中第7项为________.
210x6 [T7=C(-x)6=210x6.]
4.化简:C2n+C2n-1+…+C2n-k+…+C=________.
3n [原式=(1+2)n=3n.]
5.设(x-)n的展开式中第二项和第四项的系数之比为1∶2,求含x2的项.
[解] (x-)n的展开式中第二项和第四项分别为:
T2=C·xn-1(-)=-nxn-1,
T4=C·xn-3·(-)3=-2Cxn-3.
由题意可知=,即n2-3n-4=0,
又n∈N+,解得n=4.
设(x-)4的展开式中含x2的项为第k+1项,
则Tk+1=C·x4-k·(-)k(k=0,1,2,3,4)
根据题意可知4-k=2,解得k=2.
所以(x-)4的展开式中含x2的项为T3=C·x2·(-)2=12x2.
人教B版 (2019)选择性必修 第二册第四章 概率与统计4.1 条件概率与事件的独立性4.1.2 乘法公式与全概率公式课文内容课件ppt: 这是一份人教B版 (2019)选择性必修 第二册第四章 概率与统计4.1 条件概率与事件的独立性4.1.2 乘法公式与全概率公式课文内容课件ppt,文件包含人教B版高中数学选择性必修第二册412《乘法公式》第1课时课件ppt、人教B版高中数学选择性必修第二册412《乘法公式》第1课时教案doc等2份课件配套教学资源,其中PPT共37页, 欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第二册3.3 二项式定理与杨辉三角示范课课件ppt: 这是一份高中数学人教B版 (2019)选择性必修 第二册3.3 二项式定理与杨辉三角示范课课件ppt,文件包含人教B版高中数学选择性必修第二册33《二项式系数的性质杨辉三角和二项式定理的应用》第2课时课件ppt、人教B版高中数学选择性必修第二册33《二项式系数的性质杨辉三角和二项式定理的应用》第2课时教案doc等2份课件配套教学资源,其中PPT共51页, 欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第二册第三章 排列、组合与二项式定理3.1 排列与组合3.1.3 组合与组合数图文ppt课件: 这是一份高中数学人教B版 (2019)选择性必修 第二册第三章 排列、组合与二项式定理3.1 排列与组合3.1.3 组合与组合数图文ppt课件,文件包含人教B版高中数学选择性必修第二册313《组合与组合数》第1课时课件ppt、人教B版高中数学选择性必修第二册313《组合与组合数》第1课时教案doc等2份课件配套教学资源,其中PPT共40页, 欢迎下载使用。













