扬州卷——【江苏省专用】2022-2023学年苏科版数学八年级下册期中模拟检测卷（原卷版+解析版）

2022-2023学年江苏省扬州市八年级下册数学期中检测卷

考试时间：120分钟 试卷满分：150分 考试范围：第7-10章

姓名：___________班级：___________考号：___________

一．选择题（共8小题，满分24分，每小题3分）

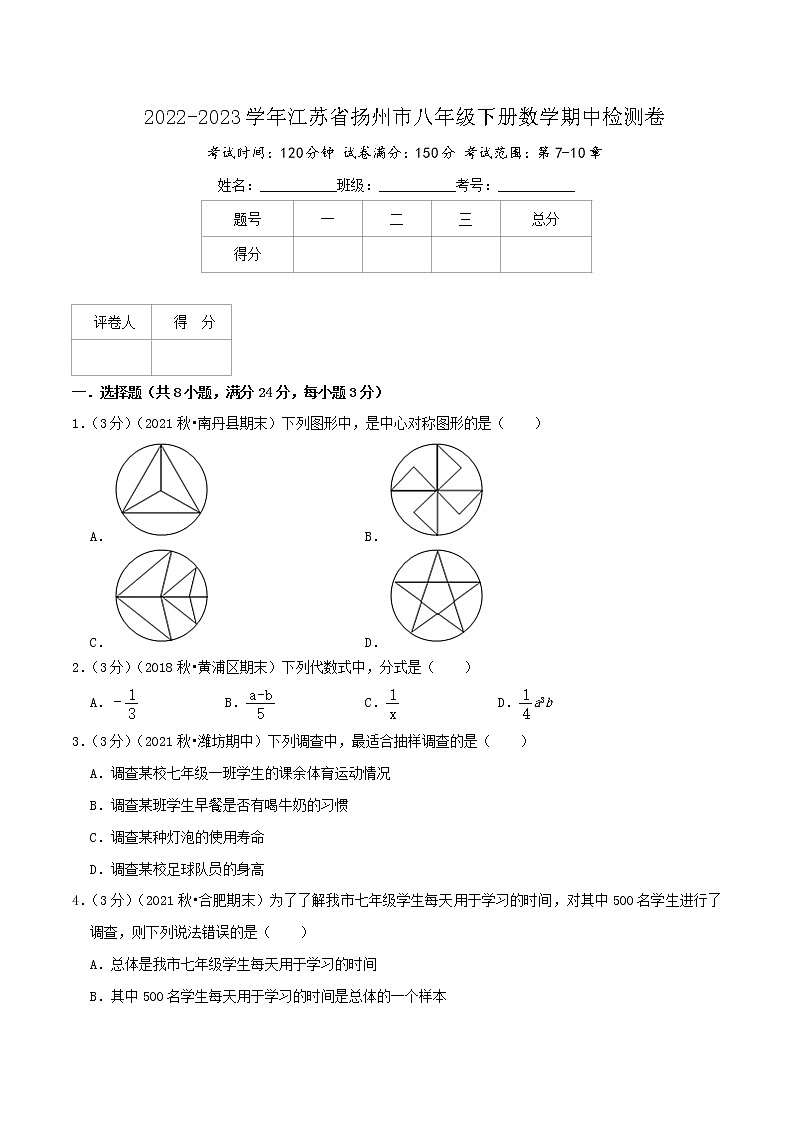
1．（3分）（2021秋•南丹县期末）下列图形中，是中心对称图形的是（　　）

A． B． 

C． D．

2．（3分）（2018秋•黄浦区期末）下列代数式中，分式是（　　）

A．﹣ B． C． D．a3b

3．（3分）（2021秋•潍坊期中）下列调查中，最适合抽样调查的是（　　）

A．调查某校七年级一班学生的课余体育运动情况 

B．调查某班学生早餐是否有喝牛奶的习惯 

C．调查某种灯泡的使用寿命 

D．调查某校足球队员的身高

4．（3分）（2021秋•合肥期末）为了了解我市七年级学生每天用于学习的时间，对其中500名学生进行了调查，则下列说法错误的是（　　）

A．总体是我市七年级学生每天用于学习的时间 

B．其中500名学生每天用于学习的时间是总体的一个样本 

C．样本容量是500名 

D．个体是500名学生中每名学生每天用于学习的时间

5．（3分）（2021春•皇姑区期末）下列各式与分式相等的是（　　）

A． B． C． D．

6．（3分）（2016•河北）关于▱ABCD的叙述，正确的是（　　）

A．若AB⊥BC，则▱ABCD是菱形 

B．若AC⊥BD，则▱ABCD是正方形 

C．若AC＝BD，则▱ABCD是矩形 

D．若AB＝AD，则▱ABCD是正方形

7．（3分）（2020秋•南充期末）如图，在△ABC中，∠ACB＝105°，将△ABC绕着点C顺时针方向旋转到△A′B′C，A′B′经过点 A．若AB′＝AC，则∠B的度数为（　　）

A．20° B．25° C．30° D．35°

8．（3分）（2016•石家庄一模）如图，在甲、乙两张太小不同的8×8方格纸上，分别画有正方形ABCD和PQMN，其顶点均在格点上，若S正方形ABCD＝S正方形PQMN，则甲、乙两张方格纸的面积之比是（　　）

A．3：4 B．4：5 C．15：16 D．16：17

二．填空题（共10小题，满分30分，每小题3分）

9．（3分）（2021春•西湖区期末）当x＝　   　时，＝0．

10．（3分）（2022秋•宁波期末）下表是某批次口罩在产品质量抽测中的检测结果．

则在这批次口罩中随机抽取一个口罩，合格的概率可估计为 　   　．

11．（3分）（2023•秦都区校级一模）如图，在▱ABCD中，连接AC，AC恰好与BC垂直，BC＝6，AC＝3，点O是对角线AC上一动点（不与点A、C重合），过点O作OE⊥AC，交CD于点E，连接BE，点F是BE的中点，连接OF，则OF的最小值为 　   　．

12．（3分）（2021春•道县期末）道县县城进行“城区改造”活动，在整个城区种植树苗5000株，树苗的成活率为90%，则成活的树苗大约有 　   　株．

13．（3分）（2023春•海陵区校级月考）已知，则分式的值为 　   　．

14．（3分）（2019秋•思明区校级期中）如图，已知正方形ABCD中，AC为对角线，点E在边AB上，点F在边BC上，AE+FC＝EF，DE、DF与AC分别交于点M、N，AM＝4，NC＝2，则MN＝　   　．

15．（3分）（2021•惠安县模拟）如图，矩形ABCD的边长AB＝1，BC＝2．将线段BC绕点B逆时针旋转，使点C恰好落在AD上的点E处，则的长是 　   　．（结果保留π）

16．（3分）（2021春•赣榆区期中）如图，连接四边形ABCD各边中点，得到四边形EFGH，当四边形ABCD的对角线AC与BD满足 　   　条件时，就能保证四边形EFGH是菱形．

17．（3分）（2022秋•烟台期末）已知关于x的方程有增根，则m＝　   　．

18．（3分）（2020秋•南通月考）如图，已知正方形ABCD的边长为3，点E是AB边上一动点，连接ED，将ED绕点E顺时针旋转90度到EF，连接DF，CF，则DF+CF的最小值是　   　．

三．解答题（共10小题，满分96分）

19．（8分）（2022秋•青云谱区校级期末）解方程．

（1）＝．                （2）+2＝．

20．（8分）（2020•宁津县二模）先化简，再求值：（﹣1）÷，其中m＝2．

21．（8分）（2020春•黄浦区期末）如图，直角坐标平面内，△OAB中A（2，3），B（5，﹣1），将△OAB绕点O逆时针旋转90°△OA'B'，点A、B分别转到A'、B'．

（1）在图中画出△OA'B'图象；

（2）求△OA'B'的面积．

22．（8分）（2021春•老河口市期末）疫情期间我市为加强学生的安全防护意识，组织了全市初中学生参加防护知识竞赛．为了了解此次知识竞赛成绩的情况，随机抽取了部分参赛学生的成绩，整理并制作出了不完整的统计表和统计图（如图），请根据图表信息解答以下问题．

（1）一共抽取了 　   　个参赛学生的成绩；表中a＝　   　；组距是 　   　；

（2）补全频数分布直方图；

（3）计算扇形统计图中“甲”对应的百分比是多少？

（4）若成绩在80分以上（包括80分）的为“优”，估计全市15000名初中学生成绩为“优”的有多少人？

23．（8分）（2022秋•永兴县期末）永州市万达广场筹建之初的一项挖土工程招标时，接到甲、乙两个工程队的投标书，每施工一天，需付甲工程队工程款2.4万元，付乙工程队工程款1.8万元，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：

（方案一）甲队单独完成这项工程，刚好按规定工期完成：

（方案二）乙队单独完成这项工程要比规定工期多用6天；

（方案三）若由甲、乙两队合作做5天，剩下的工程由乙队单独做，也正好按规定工期完工．

（1）请你求出完成这项工程的规定时间；

（2）如果你是工程领导小组的组长，为了节省工程款，同时又能如期完工，你将选择哪一种方案？说明理由．

24．（8分）（2022•海珠区校级模拟）如图，B，E，C，F在一条直线上，已知AB∥DE，AC∥DF，BE＝CF，连接AD．求证：四边形ABED是平行四边形．

25．（10分）（2020秋•六盘水期中）如图，已知平面直角坐标系中两点A（1，2）和C（5，0），且OA∥BC，AC∥OB，AC∥OB．

（1）求证：四边形OBCA为矩形；

（2）直接写出B点坐标．

26．（12分）（2020秋•开江县期末）下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程．已知：四边形ABCD是平行四边形，且AB＜BC，

求作：菱形ABEF，使点E在BC上，点F在AD上．

作法：①作∠BAD的角平分线，交BC于点E；

②以A为圆心，AB长为半径作弧，交AD于点F；

③连接EF．

则四边形ABEF为所求作的菱形．

根据小明设计的尺规作图过程：

（1）使用直尺和圆规，补全图形（保留作图痕迹）；

（2）求证四边形ABEF为菱形．

27．（12分）（2021秋•禹州市期末）下面是小明同学进行分式化简的过程，请认真阅读并解答问题：

解：．

＝第一步

＝第二步

＝÷第三步

＝÷第四步

＝•第五步

＝第六步

（1）①以上化简步骤中，第 　   　步是进行分式的通分，通分的依据是 　   　；

②第 　   　步开始出现错误，这一步错误的原因是 　   　；

（2）请写出正确的化简过程．

28．（14分）（2021春•通川区期末）如图，在平面直角坐标系中，已知点A（0，6），B（b，0），且b＜0，C，D分别是OA，AB的中点，△AOB的外角∠DBF的平分线BE与CD的延长线交于点E．

（1）求证：∠DAO＝∠DOA；

（2）①若b＝﹣8，求CE的长；

②若CE＝+1，则b＝　   　；

（3）是否存在这样的b值，使得四边形OBED为平行四边形？若存在，请求出此时四边形OBED对角线的交点坐标；若不存在，请说明理由．