2023年安徽省百校联赢名校大联考一模数学试卷

百校联赢·2023安徽名校大联考一

数学（试题卷）

注意事项：

1．你拿到的试卷满分为150分，考试时间为120分钟。

2．试卷包括“试题卷”和“答题卷”两部分，请务必在“答题卷”上答题，在“试题卷”上答题是无效的。

3．考试结束后，请将“试题卷”和“答题卷”一并交回。

一、选择题（本大题共10小题，每小题4分，共40分）

1．下列为负数的是（        ）

A．    B．     C．0     D．－1

2．一根直尺和一个45°角的三角板按如图方式叠合在一起，若，则∠2的度数是（        ）

A．65°     B．56°     C．45°     D．28°

3．2022年全国粮食总产量约13700亿斤，比上年增加73.6亿斤，这里“13700亿”用科学记数法表示为（        ）

A．   B．   C．   D．

4．如图是某几何体的三视图，该几何体是（        ）

A．    B．    C．    D．

5．估算的值在（        ）

A．3～4之间    B．4～5之间    C．5～6之间    D．6～7之间

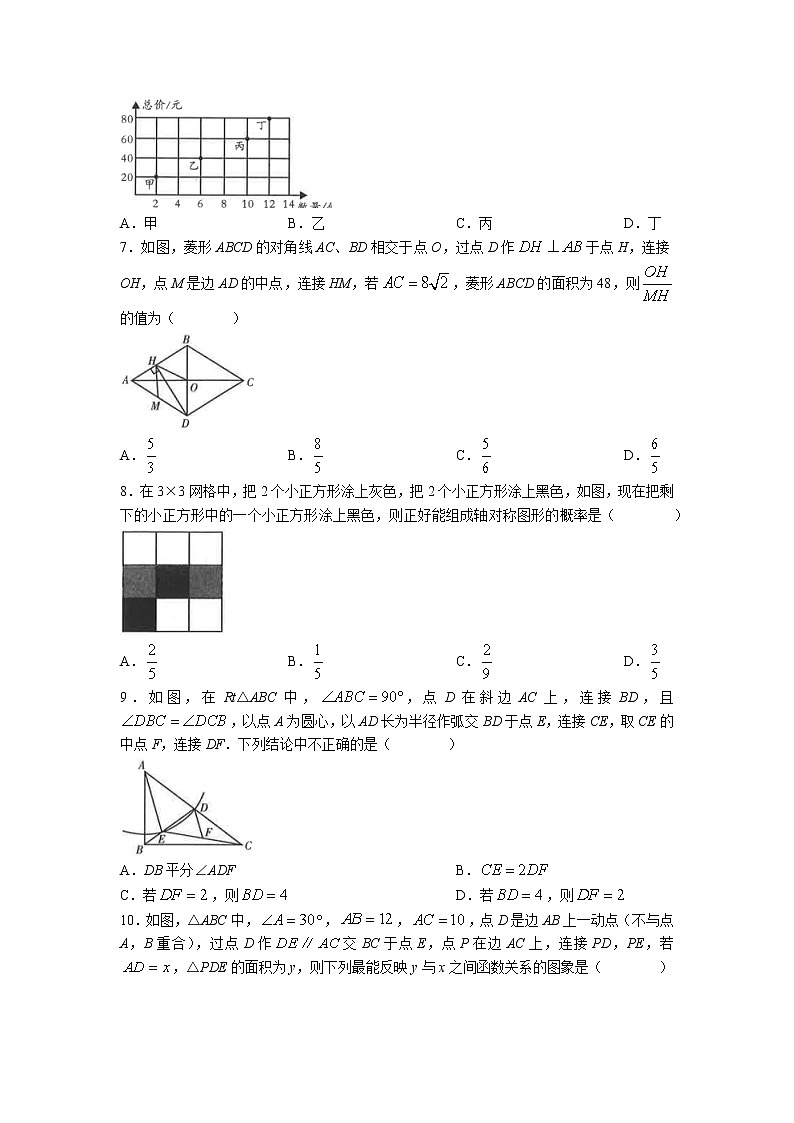
6．某人在甲、乙、丙、丁四个超市购买某品牌商品的总价和购买数量如图所示，按平均单价计算，购买该品牌商品最划算的超市是（        ）

A．甲     B．乙     C．丙     D．丁

7．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作于点H，连接OH，点M是边AD的中点，连接HM，若，菱形ABCD的面积为48，则的值为（        ）

A．     B．     C．     D．

8．在3×3网格中，把2个小正方形涂上灰色，把2个小正方形涂上黑色，如图，现在把剩下的小正方形中的一个小正方形涂上黑色，则正好能组成轴对称图形的概率是（        ）

A．     B．     C．     D．

9．如图，在Rt△ABC中，，点D在斜边AC上，连接BD，且，以点A为圆心，以AD长为半径作弧交BD于点E，连接CE，取CE的中点F，连接DF．下列结论中不正确的是（        ）

A．DB平分∠ADF        B．

C．若，则      D．若，则

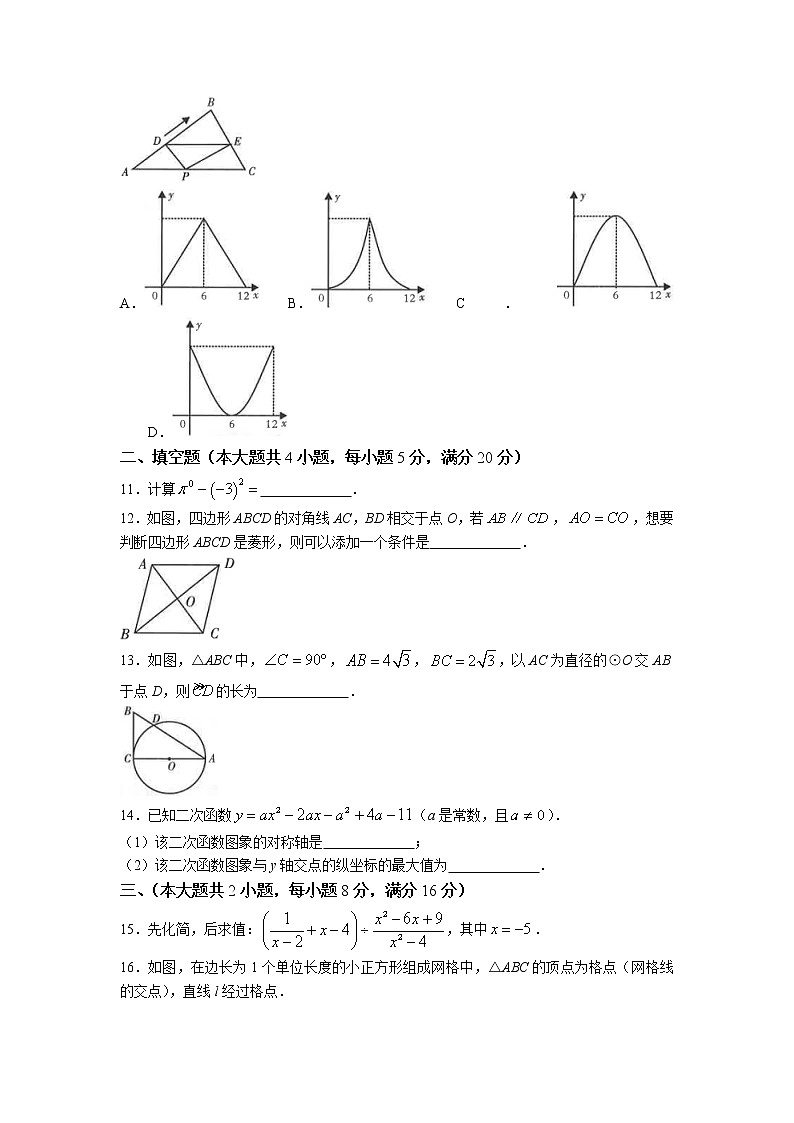
10．如图，△ABC中，，，，点D是边AB上一动点（不与点A，B重合），过点D作交BC于点E，点P在边AC上，连接PD，PE，若，△PDE的面积为y，则下列最能反映y与x之间函数关系的图象是（        ）

A． B． C． D．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．计算             ．

12．如图，四边形ABCD的对角线AC，BD相交于点O，若，，想要判断四边形ABCD是菱形，则可以添加一个条件是             ．

13．如图，△ABC中，，，，以AC为直径的⊙O交AB于点D，则的长为             ．

14．已知二次函数（a是常数，且）．

（1）该二次函数图象的对称轴是             ；

（2）该二次函数图象与y轴交点的纵坐标的最大值为             ．

三、（本大题共2小题，每小题8分，满分16分）

15．先化简，后求值：，其中．

16．如图，在边长为1个单位长度的小正方形组成网格中，△ABC的顶点为格点（网格线的交点），直线l经过格点．

（1）画出△ABC关于直线l成轴对称的．

（2）将先向下平移3个单位，再向右平移2个单位得到，请画出．

四、（本大题共2小题，每小题8分，满分16分）

17．如图，为了测量东西走向的公路桥梁AB的长度，数学兴趣小组在公路桥南侧选定观测点C，测得A在C北偏西37°方向上，点B在C的北偏东53°方向上，若测得米．求公路桥梁AB的长（精确到1米）．（参考数据，，）．

18．观察以下等式：

第1个等式；第2个等式；

第3个等式；第4个等式；……

按照以上规律，解决下列问题：

（1）写出第5个等式：                 ；

（2）写出你猜想的第n个等式（用含n的式子表示），并证明．

五、（本大题共2小题，每小题10分，满分20分）

19．点P在⊙O外，点A，C在⊙O上，连接PA，PC分别交⊙O于点B，D．

（1）如图1，若，，求∠BOD的度数；

（2）如图2，若，求证：．

20．已知，反比例函数和反比例函数如图所示．

（1）点A在反比例函数的图象上，过点A作y轴的垂线交反比例函数的图象于点B，交y轴于点M，点P在x轴上，连接PA，PB，求△PAB的面积；

（2）直线交反比例函数的图象于点C，交反比例函数的图象于点D，若，求n的值．

21．每年的12月4日是我国的“宪法宣传日”，某中学都会在这一天举行宪法知识竞赛，并随机抽取了部分学生的竞赛成绩（优秀：85～100分；良好：70～84分；合格：60～69分；不合格：59分以下）进行调查，将所得数据进行分类，统计绘制了如下不完整的统计图．请根据图中的信息，解答下列问题：

（1）本次调查的学生共             名；a＝             ；b＝             ；并补全条形统计图；

（2）本次调查的学生宪法知识竞赛成绩的中位数在哪个等次（直接写出结果）；

（3）若该校共有2800名学生，请估计该校这次宪法知识竞赛成绩在良好及以上等次的人数．

22．

如图，点在x轴上，点在y轴上，以AB为直角边作等腰直角△ABC，使，，且点C落在第一象限，二次函数的图象经过点B，C．

（1）试确定二次函数的表达式；

（2）已知点P是抛物线的对称轴上的一动点，且，求点P的坐标．

23．如图，在矩形ABCD中，点P和点M是边AD上的两个动点（点P在点M的左侧）连接BP，BM，若．

（1）求证：；

（2）已知，，

①若，求PM的长；

②若，求的值．

百校联赢·2023安徽名校大联考一

数学参考答案及评分标准

一、选择题（本大题共10小题，每小题4分，共40分）

9．B

解析：

∵，

∴，

∵，，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

∴DB平分∠ADF，

∴选项A正确；

∵，，

∴，

∴选项C正确；

∵，∴，

∴，

∴选项D正确；只有选项B不一定正确，故选B．

10．C

解析：过点D作于M，过点B作于N，

∵

∴，，

∵，

∴，

∴，

∴，

∴，

∵，

∴抛物线开口向下，又，

∴函数图象是以直线为对称轴的抛物线，位于x轴上方的部分，故选C．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．－8  12．（答案不唯一） 13．π

14．（1）直线；（2）－7

解析：

（1）该二次函数图象的对称轴是直线；

（2）当时，，

∵，

∴抛物线开口向下，

∴当时，y有最大值－7，即该二次函数图象与y轴交点的纵坐标的最大值为－7．

三、（本大题共2小题，每小题8分，满分16分）

15．解：原式，

当时，原式．

16．解：

（1）如图即为所求；

（2）如图即为所求．

四、（本大题共2小题，每小题8分，满分16分）

17．解：在△ABC中，，，

∵，

∴（米），

答：公路桥梁AB的长约为400米．

18．解：

（1）；

（2）；

证明：

∵等式左边，

等式右边，

∴等式左边＝等式右边，

∴猜想成立．

五、（本大题共2小题，每小题10分，满分20分）

19．解：

（1）如图1，连接BC，

∵，

∴，

∵，

∴，

∴；

（2）如图2，连接OP，过点O分别作于M，于N．

∵，，，

∴，

∴，

∵于M，于N，

∴，

∴．

20．解：

（1）连接OA，OB，

∵轴，

∴，，

∴，

∵轴，

∴；

（2）当时，，，，，

∴点C的横坐标为，点D的横坐标为，

∴，

∵，

∴，，

经检验，是分式方程的解，

∴．

六、（本题满分12分）

21．解：

（1）200；30；50；

C类人数为，补全条形统计图如图：

（2）本次调查的学生宪法知识竞赛成绩的中位数在“良好”等次；

（3）成绩在良好及以上等次的人数为（人）．

七、（本题满分12分）

22．解：

（1）过点C作轴于点D，

∴，

∵，，

∴，

∵，

∴，

∴，，

∵点C在第一象限，

∴点C坐标为，

∵二次函数的图象经过点B，C，

∴，解得，

∴二次函数的表达式为；

（2）∵，

∴该二次函数图象的对称轴为直线，

设点P坐标为，

∵，

∴，

∴，解得，

∴点P坐标为．

八、（本题满分14分）

23．解：

（1）在矩形ABCD中，

∴，

∴，

∵，

∴，

∵，

∴，

∴，

∴；；

（2）①∵，

∴设，则，

∴，

由（1）得，

∴，

解得，或（不合题意，舍去），

∴；

②连接CP并延长，交BM的延长线于点E．

∵，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

由勾股定理得，

由（1）得，

∴，

∴，

∴，

∵，

∴，

∴，

∴，

解得，

∴．