



- 2022-2023年苏科版数学八年级下册专项复习精讲精练:专题02 平行四边形、矩形【考点梳理+专题训练】(原卷版+解析版) 试卷 0 次下载
- 2022-2023年苏科版数学八年级下册专项复习精讲精练:专题03 菱形、正方形、三角形的中位线【考点梳理+专题训练】(原卷版+解析版) 试卷 0 次下载
- 2022-2023年苏科版数学八年级下册专项复习精讲精练:专题04 分式及分式的基本性质【考点梳理+专题训练】(原卷版+解析版) 试卷 0 次下载
- 2022-2023年苏科版数学八年级下册专项复习精讲精练:专题05 分式的加减乘除及分式方程【考点梳理+专题训练】(原卷版+解析版) 试卷 1 次下载
- 2022-2023年苏科版数学八年级下册专项复习精讲精练:期中模拟卷B卷(原卷版+解析版) 试卷 3 次下载
2022-2023年苏科版数学八年级下册专项复习精讲精练:期中模拟卷A卷(原卷版+解析版)
展开八年级期中模拟卷A卷
一.选择题(共8小题,满分16分,每小题2分)
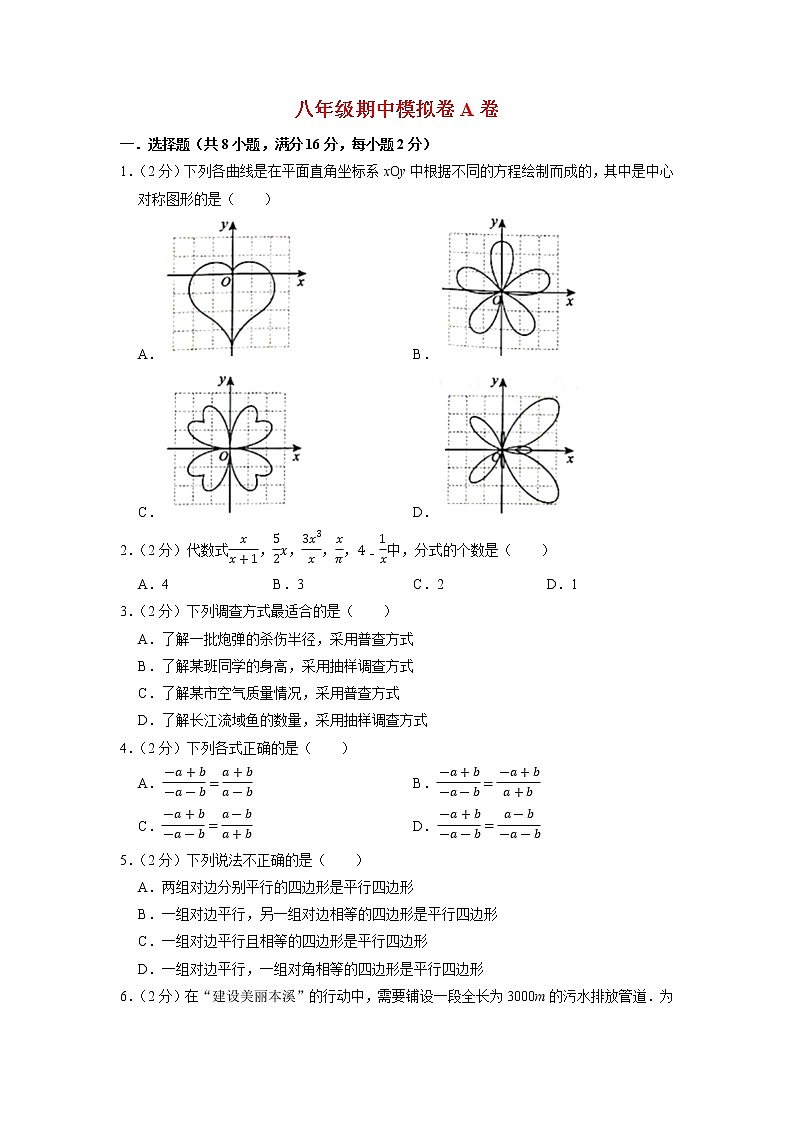
1.(2分)下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的,其中是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的概念求解.在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.这个旋转点,就叫做中心对称点.
【解答】解:选项A、B、D均不能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以不是中心对称图形,
选项C能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以是中心对称图形,
故选:C.
【点评】此题主要考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.(2分)代数式,,,,中,分式的个数是( )
A.4 B.3 C.2 D.1
【分析】分式的概念:一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫做分式.
【解答】解:代数式,,是分式,
故选:B.
【点评】本题考查分式的定义,解题的关键是熟练运用分式的定义,本题属于基础题型.
3.(2分)下列调查方式最适合的是( )
A.了解一批炮弹的杀伤半径,采用普查方式
B.了解某班同学的身高,采用抽样调查方式
C.了解某市空气质量情况,采用普查方式
D.了解长江流域鱼的数量,采用抽样调查方式
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断即可.
【解答】解:A、了解一批炮弹的杀伤半径,适合用抽样调查,A不合题意;
B、了解某班同学的身高,适合全面调查,B不合题意;
C、了解某市空气质量情况,适合用抽样调查,C不合题意;
D、了解长江流域鱼的数量,适合用抽样调查,D符合题意;
故选:D.
【点评】本题考查的是普查和抽样调查的选择.调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
4.(2分)下列各式正确的是( )
A. B.
C. D.
【分析】根据分式的基本性质化简即可.
【解答】解:
,
故选:C.
【点评】本题考查了分式的基本性质,掌握分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变是解题的关键.
5.(2分)下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
【分析】由平行四边形的判定分别对各个选项进行判断即可.
【解答】解:A、∵两组对边分别平行的四边形是平行四边形,
∴选项A不符合题意;
B、∵一组对边平行,另一组对边相等的四边形不一定是平行四边形,
∴选项B符合题意;
C、∵一组对边平行且相等的四边形是平行四边形,
∴选项C不符合题意;
D、∵一组对边平行,一组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:B.
【点评】本题考查了平行四边形的判定;熟练掌握平行四边形的判定方法是解题的关键.
6.(2分)在“建设美丽本溪”的行动中,需要铺设一段全长为3000m的污水排放管道.为了尽量减少施工时对城市交通所造成的影响,实际施工时每天的工效比原计划增加30%,结果提前30天完成这一任务.设实际每天铺x米管道.根据题意,所列方程正确的是( )
A.30
B.30
C.30
D.30
【分析】根据题意可以列出相应的分式方程,从而可以解答本题.
【解答】解:设实际每天铺xm管道,则原计划每天铺m管道,
根据题意,得30,
故选:B.
【点评】本题考查由实际问题抽象出分式方程,解答本题的关键是明确题意,列出相应的方程.
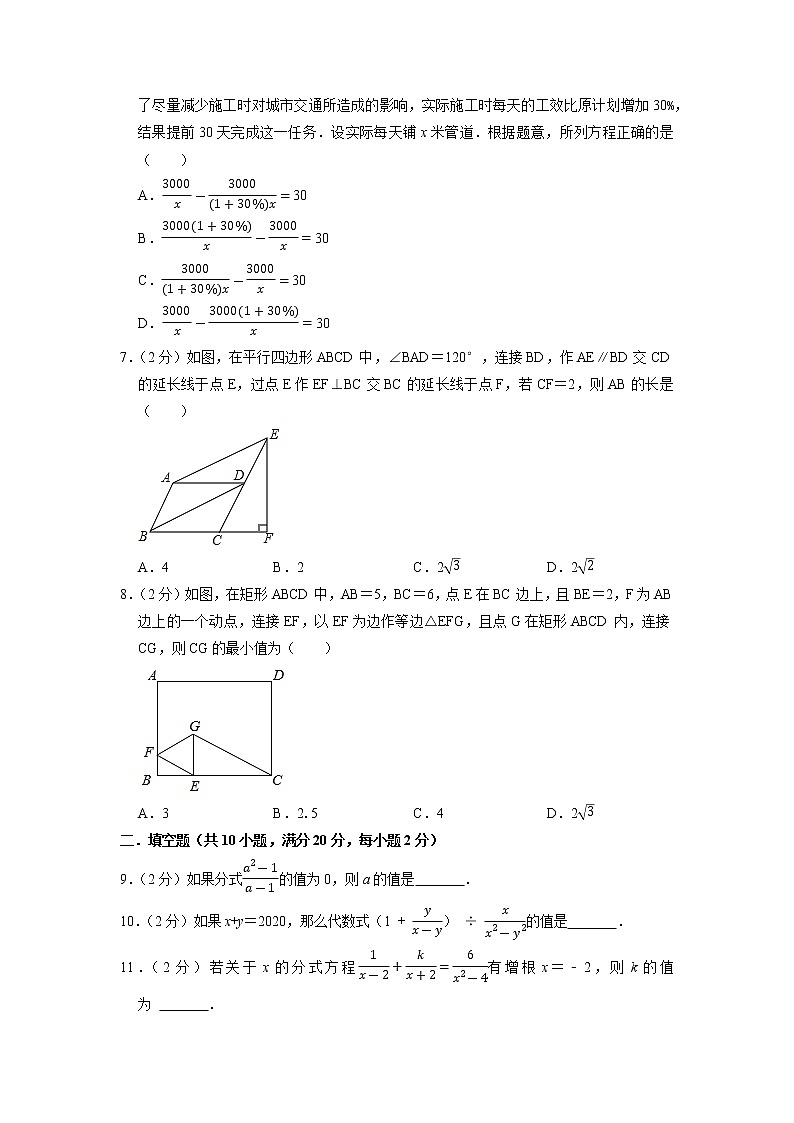
7.(2分)如图,在平行四边形ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB的长是( )
A.4 B.2 C.2 D.2
【分析】易证四边形ABDE是平行四边形,得出AB=DE,证出CE=2AB,求出∠CEF=30°,得出CE=2CF=4,即可得出AB的长.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CE=2AB,
∵∠BCD=∠BAD=120°,
∴∠ECF=60°,
∵EF⊥BC,
∴∠CEF=30°,
∴CE=2CF=4,
∴AB=2.
故选:B.
【点评】本题考查了平行四边形的性质与判定、直角三角形的性质;熟练掌握平行四边形的判定与性质是解决问题的关键.
8.(2分)如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A.3 B.2.5 C.4 D.2
【分析】以EC为边作等边三角形ECH,过点H作HN⊥BC于N,HM⊥AB于M,可证四边形MHNB是矩形,可证MH=BN,由“SAS”可证△FEH≌△GEC,可得FH=GC,当FH⊥AB时,FH有最小值,即GC有最小值,即可求解.
【解答】解:如图,以EC为边作等边三角形ECH,过点H作HN⊥BC于N,HM⊥AB于M,
又∵∠ABC=90°,
∴四边形MHNB是矩形,
∴MH=BN,
∵BE=2,
∴EC=4,
∵△EHC是等边三角形,HN⊥EC,
∴EC=EH=4,EN=NC=2,∠HEC=60°,
∴BN=4=MH,
∵△FGE是等边三角形,
∴FE=GE,∠FEG=60°=∠HEC,
∴∠FEH=∠GEC,
在△FEH和△GEC中,
,
∴△FEH≌△GEC(SAS),
∴FH=GC,
∴当FH⊥AB时,FH有最小值,即GC有最小值,
∴点F与点M重合时,FH=HM=4,
故选:C.
【点评】本题考查了旋转的性质,矩形的判定和性质,全等三角形的判定和性质,等边三角形的性质等知识,添加恰当辅助线构造全等三角形是解题的关键.
二.填空题(共10小题,满分20分,每小题2分)
9.(2分)如果分式的值为0,则a的值是 ﹣1 .
【分析】分式值为零的条件是分子等于零且分母不等于零.
【解答】解:∵分式的值为0,
∴a2﹣1=0且a﹣1≠0.
解得:a=﹣1.
故答案为:﹣1.
【点评】本题主要考查的是分式值为零的条件,掌握分式值为零的条件是解题的关键.
10.(2分)如果x+y=2020,那么代数式(1)的值是 2020 .
【分析】先计算括号内的加法,再把除法变成乘法,算乘法,最后求出答案即可.
【解答】解:
=x+y,
∵x+y=2020,
∴原式=2020,
故答案为:2020.
【点评】本题考查了分式的化简求值,正确根据分式的运算法则进行化简是解题的关键.
11.(2分)若关于x的分式方程有增根x=﹣2,则k的值为 .
【分析】把x=﹣2代入整式方程中进行计算即可解答.
【解答】解:,
x+2+k(x﹣2)=6,
把x=﹣2代入x+2+k(x﹣2)=6中得:
﹣2+2+(﹣4k)=6,
∴k,
故答案为:.
【点评】本题考查了分式方程的增根,把x=﹣2代入整式方程中进行计算是解题的关键.
12.(2分)为了了解某地初二年级男生的身高情况,某班40名学生的身高如下表,则m的值为 5 .
分组 | 147.5~155.5 | 155.5~163.5 | 163.5~171.5 | 171.5~179.5 |
频数 | 6 | 11 |
| m |
频率 |
|
| 0.45 |
|
【分析】根据频率0.45,即可求此组的人数,然后即可求解.
【解答】解:根据表格身高在163.5~171.5的频率是0.45.
∴身高在163.5~171.5的人数为:0.45×40=18(人).
∴m=40﹣6﹣11﹣18=5.
故答案为:5.
【点评】本题考查频率的定义,涉及到频数基本知识,属于基础题.
13.(2分)如图,在平行四边形ABCD中,已知AD=8cm,BE=2cm,DE平分∠ADC交BC边于点E,则AB= 6 cm.
【分析】由平行四边形的性质得出BC=AD=8cm,CD=AB,AD∥BC,再证出∠EDC=∠DEC,得出CD=CE=AB,即可得出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,CD=AB,AD∥BC,
∴∠EDA=∠DEC,
又∵DE平分∠ADC,
∴∠EDC=∠ADE,
∴∠EDC=∠DEC,
∴CD=CE=AB,
∴AB=CE=BC﹣BE=8﹣2=6(cm),
故答案为:6.
【点评】本题考查了平行四边形性质、平行线的性质、角平分线定义、等腰三角形的判定等知识;熟练掌握平行四边形的性质,证出CD=CE=AB是解题的关键.
14.(2分)如图,在由菱形和正方形组成的装饰图案中,已知菱形ABCD的面积是500cm2,正方形DEBF的面积是200cm2,则边AD的长是 5 cm.
【分析】连接BD、AC,交点为O,根据正方形DEBF的面积是200cm2,可得DF=BF=10,由勾股定理可得BD的长,进行得AC的长,然后根据菱形的性质及勾股定理可得答案、
【解答】解:连接BD、AC,交点为O,
∵四边形ABCD为菱形,
∴AC⊥BD,
∵正方形DEBF的面积是200cm2,
∴DF=BF=10(cm),
∴BD20(cm)),
∵菱形ABCD的面积是500cm2,
∴20×AC=500,
∴AC=50(cm),
∴AD5(cm).
故答案为:5.
【点评】此题考查的是正方形、菱形的性质,正确作出辅助线是解决此题的关键.
15.(2分)若分式方程的无解,则a= ﹣1或 .
【分析】先解分式方程得x,再由方程无解可得3或a+1=0,求出a的值即可.
【解答】解:,
1﹣(x﹣3)=ax,
1﹣x+3=ax,
﹣x﹣ax=﹣1﹣3,
(a+1)x=4,
x,
∵方程无解,
∴3或a+1=0,
∴a或a=﹣1,
故答案为:﹣1或.
【点评】本题考查分式方程的解,熟练掌握分式方程的解法,掌握分式方程无解的条件是解题的关键.
16.(2分)在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF= 2 .
【分析】取BC的中点G,连接EG、FG,根据三角形的中位线平行于第三边并且等于第三边的一半求出EG、FG,并求出EG⊥FG,然后利用勾股定理列式计算即可得解.
【解答】解:如图,取BC的中点G,连接EG、FG,
∵E、F分别是边AB、CD的中点,
∴EG∥AC且EGAC4=2,FG∥BD且FGBD8=4,
∵AC⊥BD,
∴EG⊥FG,
∴EF.
故答案为:2
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.
17.(2分)如图,正方形ABCD的边长是6,对角线的交点为O,点E在边CD上且CE=2,CF⊥BE,连接OF,则:
(1)∠OFB 45° ;
(2)OF= .
【分析】(1)在BE上截取BG=CF,根据正方形性质,得BO=CO,∠BOC=90°,∠OBC=∠OCD=45°,再根据同角的余角相等,得∠OBG=∠FCO,从而证明△OBG≌△OCF(SAS),进而得到∠OFG=∠OGF=45°;
(2)在Rt△BCE中,根据勾股定理,得BE=2,再根据等面积法求出CF=BG,再通过两次勾股定理的应用得出OF.
【解答】解:(1)在BE上截取BG=CF,
∵在正方形ABCD,AC⊥BD,∠ABC=∠BCD=90°,AC=BD,BOBD,COAC,AC、BD分别平分∠ABC、∠BCD,
∴BO=CO,∠BOC=90°,∠OBC=∠OCD=45°,
∵CF⊥BE,
∴∠CFE=90°,
∴∠FEC+∠ECF=90°,
∵∠EBC+∠FEC=90°,
∴∠EBC=∠ECF,
∴∠OBC﹣∠EBC=∠OCD﹣∠ECF,
∴∠OBG=∠FCO,
∴△OBG≌△OCF(SAS),
∴∠BOG=∠FOC,OG=OF,
∴∠GOC+∠COF=90°,
∴∠OFG=∠OGF=45°,
故答案为:45°;
(2)在Rt△BCE中,根据勾股定理,得BE=2,
∴CF=BG,
在Rt△FCE中,根据勾股定理,得EF,
∴GF=BE﹣BG﹣EF,
在Rt△FCE中,根据勾股定理,得OF,
故答案为:.
【点评】本题主要考查了正方形性质、全等三角形的判定与性质、勾股定理,掌握这三个性质定理的综合应用,其中勾股定理的应用是解题关键.
18.(2分)如图,已知正方形ABCD中,AD=6,∠DAE=30°,点F为AE的中点,过点F作直线分别与AD、BC相交于点M、N,若MN=AE,则AM的长等于 4或2 .
【分析】在正方形ABCD中,根据AD=6,∠DAE=30°,可得AE=4,点F为AE的中点,可得AF=EF=2,分两种情况:①过M作MG⊥BC,G为垂足,则MG=DC=AD,证明Rt△MGN≌Rt△ADE,利用勾股定理可得AM的长;②如图,过N作NG⊥AD于G,过M作MH⊥AE于H,设MH=x,则AM=2x,AH=FHx,利用含30度角的直角三角形,进而可得AM的长.
【解答】解:在正方形ABCD中,AD=6,∠DAE=30°,
设DE=x,则AE=2x,由勾股定理x2+62=(2x)2,
解得:x=2(负值舍去),
∴AE=4,
∵点F为AE的中点,
∴AF=EF=2,
分两种情况:
①过M作MG⊥BC,G为垂足,则MG=DC=AD,
在Rt△MGN和Rt△ADE中,
,
∴Rt△MGN≌Rt△ADE(HL),
∴∠NMG=∠EAD,
∴∠NMG+∠AMF=90°,
∴∠EAD+∠AMF=90°,
∴∠AFM=90°,
在Rt△AFM中,∠DAE=30°,AF=2,
设MF=m,则AM=2m,
由勾股定理,得
4m2﹣m2=12,
解得m=2(负值舍去),则AM=4;
②方法一:根据对称性由①可知:AM=6﹣4=2,
方法二:如图,过N作NG⊥AD于G,过M作MH⊥AE于H,
则NG=CD=AD,
在Rt△ADE和Rt△NGM中,
,
∴Rt△ADE≌Rt△NGM(HL),
∴∠GNM=∠DAE=30°,
∴∠GMN=60°,
△AMF中,∠GMN=∠MAF+∠AFM,
∴∠AFM=∠DAE=30°,
∴AM=MF,
∵MH⊥AF,
∴AH=FH,
设MH=x,则AM=2x,AH=FHx,
∵F是AE的中点,
∴AE=2AF=4AH=4x,
Rt△ADE中,∠DAE=30°,
∴DEAE=2x,ADDE=6x,
∵AD=6,即6x=6,
x=1,即AM=2x=2;
故答案为:4或2.
【点评】本题是四边形的综合题,考查的是正方形的性质、全等三角形的判定与性质、含30度角的直角三角形等知识,作辅助线,构建三角形全等是关键,学会构建方程解决问题,属于中考填空的压轴题.
三.解答题(共8小题,满分64分,每小题8分)
19.(8分)(1)计算:();
(2)解方程:1.
【分析】(1)根据分式的混合运算顺序即可计算;
(2)根据分式方程的解题过程进行计算即可.
【解答】解:(1)原式
;
(2)方程两边同时乘以(x﹣1)(x+2)得:
x(x+2)﹣3=(x﹣1)(x+2),
x2+2x﹣3=x2+x﹣2,
x=1.
检验:把x=1代入(x﹣1)(x+2)=0,
所以原分式方程无解.
【点评】本题考查了解分式方程,分式的混合运算,解决本题的关键是掌握解分式方程的方法.
20.(6分)先化简,再求值(x+1),其中整数x满足﹣1≤x<3.
【分析】根据分式的减法和除法可以化简题目中的式子,然后从﹣1≤x<3中选取使得原分式有意义的整数代入化简后的式子即可解答本题.
【解答】解:(x+1)
,
∵x(x+1)≠0,
∴x≠0,x≠﹣1,
∵整数x满足﹣1≤x<3,
∴x=1或2,
当x=1时,原式1,
当x=2时,原式.
【点评】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
21.(8分)如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C.
(2)平移△ABC,使点A的对应点A2坐标为(﹣3,﹣4),请画出平移后对应的△A2B2C2.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
【分析】(1)利用中心对称的性质写出A、B关于C点的对称点,然后描点即可;
(2)利用点A、A2的坐标特征确定平移的方向与距离,然后利用此平移规律写出B2、C2的坐标,然后描点即可;
(3)连接A1A2交BB2于P点,则P点为旋转中心.
【解答】解:(1)如图,△A1B1C为所作;
(2)如图,△A2B2C2为所作;
(3)如图,△A2B2C2为所作,旋转中心P的坐标为(0,﹣1).
【点评】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.
22.(8分)如图,▱ABCD的对角线AC、BD相交于点O,且OE=OF.
(1)求证:△BOE≌△DOF;
(2)求证:BE∥DF.
【分析】(1)由平行四边形的性质得出OB=OD,由SAS证明△BOE≌△DOF即可;
(2)先证明四边形EBFD是平行四边形,由平行四边形的性质可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(SAS);
(2)连接DE、BF,
由(1)知△BOE≌△DOF,
∴OB=OD,OE=OF,
∴四边形EBFD是平行四边形,
∴BE∥DF.
【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的判定与性质是解决问题的关键.
23.(8分)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“停课不停学”的要求,各地学校也都开展了远程网络教学,历下区某校为学生提供四类在线学习方式:
在线阅读、在线听课、在线答疑、在线讨论.为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
根据上面提供的信息,回答下列问题:
(1)本次接受问卷调查的学生共有 100 人,在扇形统计图中“在线听课”所占的百分比为 40% ,在扇形统计图中“在线讨论”所对应扇形圆心角为 54 度.
(2)请补全条形统计图;
(3)若该校共有800名学生,请你估计该校学生对“在线听课”和“在线答疑”感兴趣的共有多少人?
【分析】(1)由在线阅读人数及其所占百分比求出总人数;用“在线听课”的人数除以总人数可得在扇形统计图中“在线听课”所占的百分比;用360°乘“在线讨论”所占百分比可得在线讨论”所对应扇形圆心角度数;
(2)根据四种方式的人数之和等于总人数求出在线答疑人数,从而补全图形;
(3)用总人数乘以样本中“在线听课”和“在线答疑”感兴趣人数所占比例可得答案.
【解答】解:(1)25÷25%=100(人),
∴本次调查的人数为100人;
在扇形统计图中“在线听课”所占的百分比为:40%;
在扇形统计图中“在线讨论”所对应扇形圆心角为:360°54°.
故答案为:100;40%;54;
(2)在线答疑”的人数为:100﹣25﹣40﹣15=20(人),
补全条形统计图如图所示:
(3)800480(名).
答:估计该校学生对“在线听课”和“在线答疑”感兴趣的共有480人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.从两个统计图中获取数量和数量之间的关系是解决问题的关键,样本估计总体是统计中常用的方法.
24.(8分)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E.延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形:
(2)连接OE,若AD=20,EC=8.求OE的长度.
【分析】(1)由菱形的性质得AD∥BC且AD=BC,再证BC=EF,则四边形AEFD是平行四边形,然后由矩形的判定定理即可得到结论;
(2)由菱形的性质得AD=AB=BC=20,再由勾股定理求出AE=16,AC=8,然后由直角三角形斜边上的中线性质即可得出答案.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=20,
∴AD=AB=BC=20,
∵EC=8,
∴BE=20﹣8=12,
在Rt△ABE中,AE16,
在Rt△AEC中,AC8,
∵四边形ABCD是菱形,
∴OA=OC,
∵AE⊥BC,
∴∠AEC=90°,
∴OEAC=4.
【点评】本题考查了矩形的判定和性质,菱形的性质,勾股定理,直角三角形斜边上的中线性质等知识,熟练掌握矩形的判定与性质是解题的关键.
25.(8分)疫情防控期间,某班级购买一批消毒液供学生使用,有甲,乙两种不同消毒液供选择.已知甲种消毒液比乙种消毒液每瓶贵3元,用360元单独购买其中一种消毒液时,可以比单独购买另一种消毒液多6瓶.
(1)问甲,乙两种消毒液的单价是多少?
(2)若用360元(钱用完)购买两种消毒液,且甲种消毒液不少于16瓶,问有几种购买方案(两种消毒液都要有)?请通过计算说明.
【分析】(1)设甲种消毒液的单价为x元,则乙种消毒液的单价为(x﹣3)元,由题意:用360元单独购买其中一种消毒液时,可以比单独购买另一种消毒液多6瓶.列出分式方程,解方程即可;
(2)设购买甲种消毒液m瓶,乙种消毒液n瓶,由题意:用360元(钱用完)购买两种消毒液,列出二元一次方程,求出正整数解(m≥16),进而得出答案.
【解答】解:(1)设甲种消毒液的单价为x元,则乙种消毒液的单价为(x﹣3)元,
由题意得:6,
解得:x=15,
经检验,x=15是原方程的解,
则x﹣3=12,
答:甲种消毒液的单价为15元,乙种消毒液的单价为12元;
(2)设购买甲种消毒液m瓶,乙种消毒液n瓶,
由题意得:15m+12n=360,
∵m≥16,且m、n为正整数,
∴或,
∴有2种购买方案:
①购买甲种消毒液20瓶,乙种消毒液5瓶;
②购买甲种消毒液16瓶,乙种消毒液10瓶.
【点评】本题考查了分式方程的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,列出分式方程;(2)找准等量关系,列出二元一次方程.
26.(10分)已知长方形ABCO,O为坐标原点,B的坐标为(8,6),点A,C分别在坐标轴上,P是线段BC上的动点,设PC=m,
(1)已知点D在第一象限且是直线y=2x+6上的一点,设D点横坐标为n,则D点纵坐标可用含n的代数式表示为 2n+6 ,此时若△APD是等腰直角三角形,求点D的坐标;
(2)直线y=2x+b过点(3,0),请问在该直线上,是否存在第一象限的点D使△APD是等腰直角三角形?若存在,请直接写出这些点的坐标,若不存在,请说明理由.
【分析】(1)由点D在第一象限且是直线y=2x+6上的一点,即可用含n的代数式表示D点纵坐标,y=2x+6与x轴夹角>45°,即∠DAB>45°,故∠DAP>45°,所以三角形APD是等腰直角的情况下,只能是∠DAP=90°.作DE⊥y轴于E点,作PF⊥y轴于F点,可得∠DEA=∠AFP=90°,再由三角形ADP为等腰直角三角形,得到AD=AP,利用同角的余角相等得到一对角相等,利用AAS得到△ADE≌△APF,由全等三角形的对应边相等得到AE=PF,由AE+OA求出OE的长,即为D的纵坐标,代入直线解析式求出D的横坐标,即可确定出D的坐标;
(2)存在点D,使△APD是等腰直角三角形,理由为:由直线y=2x+b过点(3,0)求出直线的解析式,分三种情况考虑:当∠ADP=90°,AD=PD时,根据等腰直角三角形的性质易得D点坐标;当∠APD=90°,AP=PD时,由全等三角形的性质表示出D点坐标为(14﹣m,m+8),列出关于m的方程,求出m的值,即可确定出D点坐标;当∠ADP=90°,AD=PD时,同理求出D的坐标,综上,得到所有满足题意D得坐标.
【解答】解:(1)如图,作DE⊥y轴于E点,作PF⊥y轴于F点,可得∠DEA=∠AFP=90°,
∴DE∥PF∥OC,
∵四边形ABCO是矩形,
∴AB∥OC,
∴AB∥PF,
∵△DAP为等腰直角三角形,
∴AD=AP,∠DAP=90°,
∴∠EAD+∠DAB=90°,∠DAB+∠BAP=90°,
∴∠EAD=∠BAP,
∵AB∥PF,
∴∠BAP=∠FPA,
∴∠EAD=∠FPA,
∵在△ADE和△PAF中,
,
∴△ADE≌△PAF(AAS),
∴AE=PF=8,OE=OA+AE=14,
设点D的横坐标为n,
∵点D在第一象限且是直线y=2x+6上的一点,
∴D点纵坐标可用含n的代数式表示为2n+6,
∴14=2n+6,得n=4,
∴点D的坐标是(4,14);
故答案为:2n+6,点D的坐标是(4,14);
(2)存在点D,使△APD是等腰直角三角形,理由为:
∵直线y=2x+b过点(3,0),
∴0=2×3+b,解得:b=﹣6,
∴直线解析式为y=2x﹣6,
当∠ADP=90°,AD=PD时,如图,作DE⊥AB于E点,作DF⊥y轴于F点,
∴DE=AE=BEAB=4,AF=DE,
∵B的坐标为(8,6),
∴OF=OA﹣AF=6﹣4=2,
∴D点坐标(4,2);
当∠APD=90°,AP=PD时,如图,作PE⊥y轴于E点,作DF⊥EP于F点,
∵PC=m,
同(1)可得△ADE≌△PAF(AAS),
∴AE=PF=6﹣m,PE=DF=AB=8,
则D点坐标为(8+6﹣m,m+8),
∵点D在直线y=2x﹣6上,
∴m+8=2(8+6﹣m)﹣6,解得m,
∴D点坐标(,);
当∠ADP=90°,AD=PD时,如图,作DE⊥y轴于E点,作PF⊥ED于F点,
同理可求得D点坐标(,),
综上,符合条件的点D存在,坐标为(4,2)或(,)或(,).
【点评】此题考查了一次函数综合题,涉及的知识有:全等三角形的判定与性质,等腰直角三角形的性质,利用了分类讨论及数形结合的思想,本题第二问注意考虑问题要全面,做到不重不漏.
2022-2023年苏科版数学七年级下册专项复习精讲精练:期中模拟预测卷03(原卷版 解析版): 这是一份2022-2023年苏科版数学七年级下册专项复习精讲精练:期中模拟预测卷03(原卷版 解析版),文件包含期中模拟预测卷03满分140分解析版docx、期中模拟预测卷03满分140分原卷版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
2022-2023年苏科版数学七年级下册专项复习精讲精练:期中模拟预测卷02(原卷版 解析版): 这是一份2022-2023年苏科版数学七年级下册专项复习精讲精练:期中模拟预测卷02(原卷版 解析版),文件包含期中模拟预测卷02满分150分解析版docx、期中模拟预测卷02满分150分原卷版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
2022-2023年苏科版数学八年级下册专项复习精讲精练:期中模拟卷B卷(原卷版+解析版): 这是一份2022-2023年苏科版数学八年级下册专项复习精讲精练:期中模拟卷B卷(原卷版+解析版),文件包含2022-2023年苏科版数学八年级下册专项复习精讲精练期中模拟卷B卷解析版docx、2022-2023年苏科版数学八年级下册专项复习精讲精练期中模拟卷B卷原卷版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。












