2022-2023年北师大版数学七年级下册专项复习精讲精练：专题01 整式的乘除（原卷版+解析版）

这是一份2022-2023年北师大版数学七年级下册专项复习精讲精练：专题01 整式的乘除（原卷版+解析版），文件包含2022-2023年北师大版数学七年级下册专项复习精讲精练专题01整式的乘除解析版docx、2022-2023年北师大版数学七年级下册专项复习精讲精练专题01整式的乘除原卷版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。
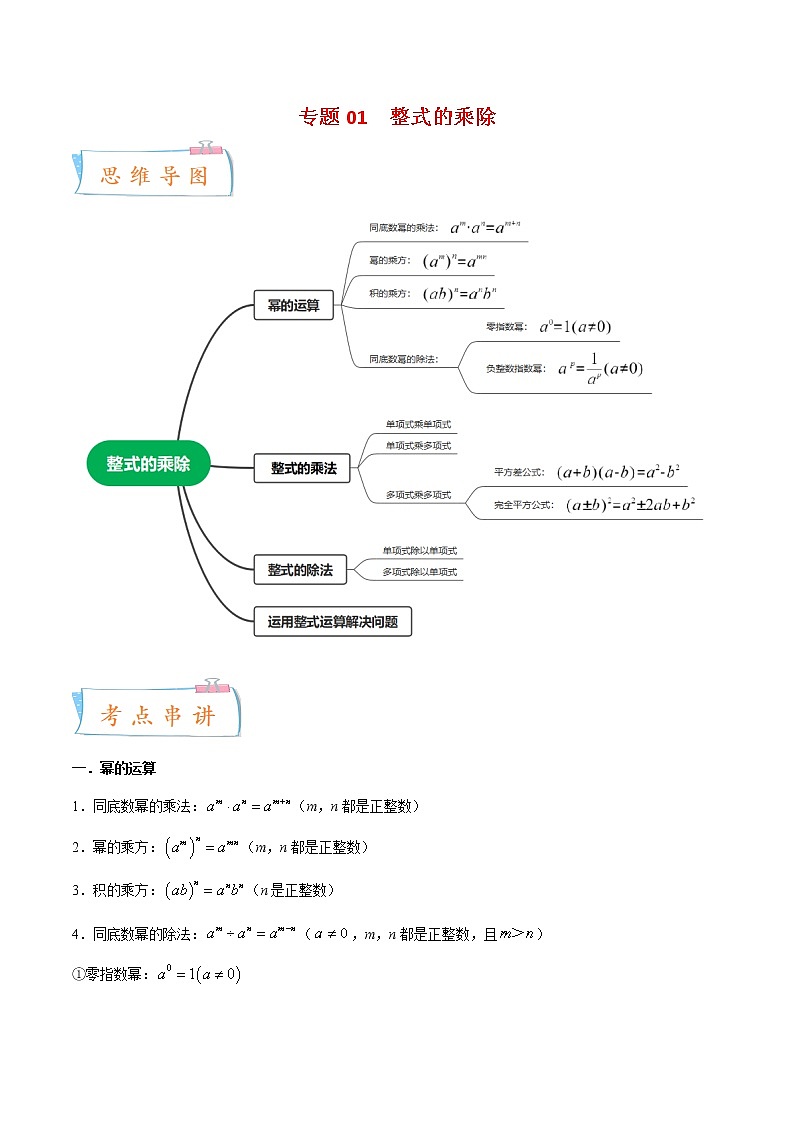
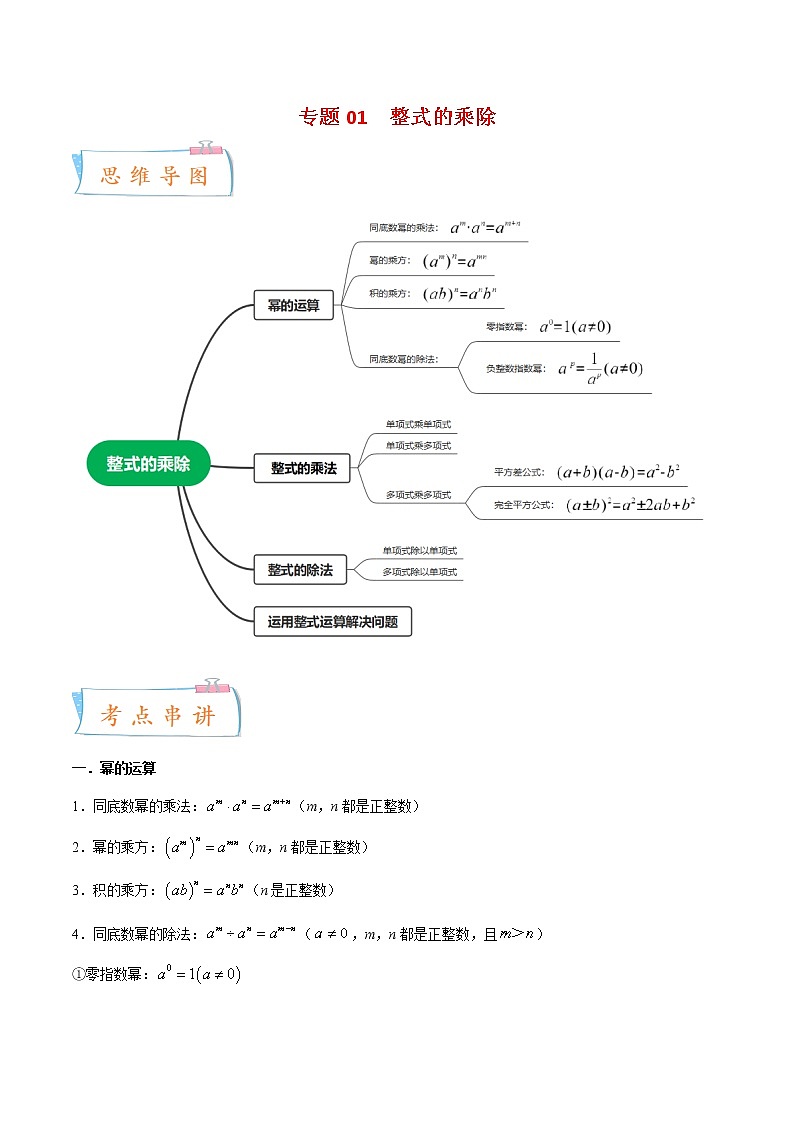
专题01  整式的乘除 一．幂的运算1．同底数幂的乘法：（m，n都是正整数）2．幂的乘方：（m，n都是正整数）3．积的乘方：（n是正整数）4．同底数幂的除法：（，m，n都是正整数，且）①零指数幂：②负整数指数幂：（，p是正整数）二．整式的乘法1．单项式乘单项式：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式．2．单项式乘多项式：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加．3．多项式乘多项式：多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加．4．两个乘法公式：①平方差公式：②完全平方公式：三．整式的除法1．单项式除以单项式：单项式与单项式相除，把它们的系数、同底数幂分别相除，作为商的因式．对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式．2．多项式除以单项式：多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加．【专题过关】一．幂的运算（共4小题）1．计算的结果是（　　）A．B．C．D．【答案】C【分析】利用幂的乘法公式“”求解．【详解】解：．故选：C．【点睛】本题考查了同底数幂的乘法运算，直接套用公式即可．2．下列运算中，正确的是（　　）A．B．C．D．【答案】C【分析】根据同底数幂的乘法法则可判断选项A，D，根据合并同类项可判断选项B，根据幂的乘方法则可判断选项C．【详解】解：A．，选项A不符合题意；B．不是同类项，不能合并，选项B不符合题意；C．，选项C符合题意；D．，选项D不符合题意；故选：C．【点睛】本题主要考查了同底数幂的乘法，幂的乘方以及合并同类项，掌握同底数幂的乘法法则，幂的乘方法则以及合并同类项法则是解题的关键．3．计算的结果是（　　）A．B．C．D．【答案】B【分析】根据积的乘方运算以及幂的乘方运算即可求出答案．【详解】解：原式，故选：B．【点睛】本题考查幂的乘方运算以及积的乘方运算，解题的关键是熟练运用幂的乘方运算以及积的乘方运算，本题属于基础题型．4．下列运算正确的是（　　）A．B．C．D．【答案】D【分析】利用合并同类项的法则，同底数幂的除法的法则，幂的乘方与积的乘方的法则对各项进行运算即可．【详解】解：A、，故A不符合题意；B、，故B不符合题意；C、，故C不符合题意；D、，故D符合题意；故选：D．【点睛】本题主要考查幂的乘方与积的乘方，同底数幂的除法，合并同类项，解答的关键是对相应的运算法则的掌握．二．幂的运算的逆用（共5题）5．若，则m＝　   　．【答案】3【分析】同底数幂相乘，底数不变，指数相加，据此解答即可．【详解】解：因为，所以，解得．故答案为：3．【点睛】本题主要考查了同底数幂的乘法，熟记幂的运算法则是解答本题的关键．6．若，，则＝　   　．【答案】b【分析】利用同底数幂的乘法的法则进行求解即可．【详解】解：∵，，∴，，．故答案为：b．【点睛】本题主要考查同底数幂的乘法，解答的关键是对相应的运算法则的掌握．7．若，，则的值为 　   　．【答案】35【分析】根据同底数幂乘法及幂的乘方的逆运算解答即可．【详解】解：∵，，∴，故答案为：35．【点睛】本题考查了同底数幂乘法、幂的乘方，运用法则逆运算是解题的关键．8．计算：＝　   　．【答案】【分析】根据积的乘方的逆运算计算即可．【详解】解：＝＝＝．故答案为：．【点睛】本题主要考查了积的乘方的逆运算及有理数的乘方运算，掌握积的乘方的逆运算及有理数的乘方运算法则是解题关键．9．如果，，那么＝　   　．【答案】45【分析】分别根据幂的乘方以及同底数幂的乘法法则解答即可．【详解】解：∵，，∴．故答案为：45．【点睛】本题主要考查了同底数幂的乘法以及幂的乘方与积的乘方，熟记幂的运算法则是解答本题的关键．三．比较幂的大小（共2题）10．比较，，的大小正确的是（　　）A．B．C．D．【答案】B【分析】把三个数化成指数相同的幂比较大小，底数大的幂大．【详解】解：；；；∵，∴．故选：B．【点睛】本题考查了有理数的大小比较，幂的乘方与积的乘方，解题的关键是掌握幂的乘法与积的乘方．11．比较大小：　   　．（填“＞”、“＜”或“＝”）【答案】＜【分析】根据幂的乘方解决此题．【详解】解：，．∵，∴．∴．故答案为：＜．【点睛】本题主要考查幂的乘方，熟练掌握幂的乘方是解决本题的关键．四．零指数幂和负整数指数幂的意义（共3题）12．若成立，则a的值为（　　）A．B．C．D．或【答案】B【分析】利用零指数幂的运算法则解题即可．【详解】解：∵，∴，解得，故选：B．【点睛】本题考查零指数幂的运算，掌握零指数幂的底数不能为零是解题的关键．13．代数式可以表示的是（　　）A．2的相反数B．2的绝对值C．2的倒数D．2与1的差【答案】C【分析】直接利用负整数指数米的幂的性质化简，结合倒数的定义得出答案．【详解】解：∵，∴代数式可以表示2的倒数．故选：C．【点睛】此题主要考查了负整数指数幂的性质以及倒数的定义，正确掌握相关定义是解题关键．14．若有意义，则x取值范围是（　　）A．B．C．且D．且【答案】D【分析】直接利用负整数指数幂的性质以及零指数幂的性质得出答案．【详解】解：若有意义，则且，解得：且．故选：D．【点睛】此题主要考查了负整数指数幂的性质以及零指数幂的性质，正确把握相关定义是解题关键．五．用科学记数法表示小于1的数（共3题）15．KN95型口罩能过滤空气中95%的粒径约为0.00000025m的非油性颗粒，用科学记数法表示0.00000025是（　　）A．B．C．D．【答案】D【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】解：0.00000025＝．故选：D．【点睛】本题考查用科学记数法表示较小的数，一般形式为，其中，n为由原数左边起第一个不为零的数字前面的0的个数所决定．16．信息技术发展的今天，芯片制造的核心是光刻技术，我国的光刻技术水平已突破到28nm，已知，则28nm用科学记数法表示是（　　）A．B．C．D．【答案】A【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．【详解】解：因为，所以．故选：A．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要确定a的值以及n的值．17．若把数字0.0000000618用科学记数法表示为的形式，则n＝　   　．【答案】【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．【详解】解：0.0000000618＝．∴．故答案为：．【点睛】此题主要考查了用科学记数法表示较小的数，一般形式为，其中，n为由原数左边起第一个不为零的数字前面的0的个数所决定．六．幂的综合运算（共5小题）18．下列运算：①；②；③；④；⑤．其中错误的是 　   　．（填写序号）【答案】①②③⑤【分析】利用同底数幂的除法的法则，同底数幂的乘法的法则，幂的乘方与积的乘方的法则对各式进行运算即可．【详解】解：①，故①符合题意；②，故②符合题意；③，故③符合题意；④，故④不符合题意；⑤，故⑤符合题意；则错误的有①②③⑤．故答案为：①②③⑤．【点睛】本题主要考查同底数幂的除法，同底数幂的乘法，积的乘方，解答的关键是对相应的运算法则的掌握．19．计算：＝　   　．【答案】1【分析】根据负整数指数幂和零指数幂运算法则，以及乘方运算法则进行计算即可．【详解】解：．【点睛】本题主要考查负整数指数幂，解题的关键是熟练掌握负整数指数幂和零指数幂运算法则，以及乘方运算法则，准确计算．20．计算：．【答案】0【分析】根据同底数幂的乘除法法则解答即可．【详解】解：．【点睛】此题考查了同底数幂的乘除法，熟练掌握同底数幂的乘除法法则是解题的关键．21．计算：（1）；（2）．【答案】（1）；（2）0【分析】（1）先算同底数幂的除法，再算同底数幂的乘法即可；（2）先算积的乘方，同底数幂的乘法，再算同底数幂的除法，最后合并同类项即可．【详解】解：（1）；（2）．【点睛】本题主要考查同底数的除法，同底数幂的乘法，积的乘方，解答的关键是对相应的运算法则的掌握．22．（1）若，求m的值；（2）已知，，求的值；（3）若n为正整数，且，求的值．【答案】（1）15；（2）；（3）80【分析】（1）把代数式化为同底数幂的除法，再进行计算即可；（2）先求出与的值，再进行计算即可；（3）先把题中化为，再把代入进行计算即可．【详解】解：（1）∵，∴，∴，解得；（2）∵，，∴，，∴；（3）∵，∴．【点睛】本题考查的是同底数幂的除法及幂的乘方与积的乘方法则，熟知以上知识是解题的关键．七．运用整式乘法进行计算（共4小题）23．计算：（1）；（2）．【答案】（1）（2）【分析】（1）先利用单项式乘多项式法则计算，再合并同类项；（2）利用多项式乘多项式法则计算．【详解】解：（1）；（2）．【点睛】本题考查了整式的混合运算，掌握单项式乘多项式、多项式乘多项式法则是解决本题的关键．24．计算：（1）；（2）．【答案】（1）（2）【分析】（1）先算积的乘方，再算单项式乘单项式；（2）根据单项式乘多项式的计算法则计算即可求解．【详解】解：（1）；（2）．【点睛】本题考查了积的乘方，单项式乘单项式，单项式乘多项式，关键是熟练掌握计算法则正确进行计算．25．计算：．【答案】【分析】根据单项式乘多项式的运算法则解答即可．【详解】解：．【点睛】此题考查了单项式乘多项式，熟练掌握单项式乘多项式的运算法则：m（a+b+c）＝ma+mb+mc是解题的关键．26．先化简，再求值：，其中．【答案】-98【分析】首先根据单项式与多项式相乘的法则去掉括号，然后合并同类项，最后代入已知的数值计算即可．【详解】解：，当时，原式．【点睛】本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．八．运用整式乘法确定字母的值（共3小题）27．若，则a＝　   　．【答案】【分析】把化为，根据等式的恒等性得出，进而求出a的值．【详解】解：∵，∴，∴，∴，故答案为：．【点睛】本题考查多项式乘多项式的运算，掌握多项式乘多项式的运算法则，等式的恒等性是解题关键．28．若与的乘积中不含x的二次项，则实数m的值为 　   　．【答案】【分析】利用多项式与多项式相乘，展开后合并同类项，再令含x的二次项系数为0，求解即可．【详解】解：，∵与的乘积中不含x的二次项，∴，解得：，∴实数m的值为．故答案为：．【点睛】本题考查了多项式与多项式的乘积，掌握多项式与多项式的乘法法则与合并同类项是关键．29．已知代数式，，．（1）化简所表示的代数式；（2）若代数式值与x的取值无关，求出a、b的值．【答案】（1）；（2），【分析】（1）把，代入，去括号，合并同类项计算即可；（2）计算，根据代数式值与x的取值无关列出方程解答即可．【详解】解：（1）∵，，∴＝＝；（2）＝＝＝．∵代数式的值与x的取值无关，∴，，∴，．【点睛】本题考查了整式的混合运算，解题的关键是掌握单项式乘多项式以及整式加减的运算法则．九．运用整式乘法解决实际问题（共3小题）30．图1是长为a，宽为b（a＞b）的小长方形纸片，将6张如图1的纸片按图2的方式不重叠地放在长方形内，已知的长度固定不变，BC的长度可以变化，图中阴影部分（即两个长方形的面积分别表示为，，若，且S为定值，则a，b满足的数量关系：　   　．【答案】【分析】设，表示出和，进一步可得，根据S为定值，可得，进一步可得a，b满足的数量关系【详解】解：设，根据题意，得，，∴，∵S为定值，∴，∴，故答案为：．【点睛】本题考查了多项式乘多项式，根据题意表示出是解题的关键．31．甲、乙两个长方形的边长如图所示，其面积分别记为，．（1）请通过计算比较与的大小；（2）若一个正方形的周长等于甲、乙两个长方形的周长的和，设该正方形的面积为，试说明代数式的值是一个常数．【答案】（1）；（2）20【分析】（1）依据长方形面积公式，分别计算出，，然后进行作差比较计算出即可判断；（2）依据题意计算出正方形的周长，从而求出及即可．【详解】解：（1），，∵，∴；（2）由题意得：正方形的边长是：，∴，∵，∴代数式的值是一个常数20．【点睛】本题考查了整式的四则混合运算；解题的关键是理解题意，正确列式计算．32．如图，某小区有一块长为米，宽为米的长方形地块，物业公司计划在小区内修一条平行四边形小路，小路的底边宽为a米，将阴影部分进行绿化．（1）用含有a、b的式子表示绿化的总面积S；（2）若，，求出此时绿化的总面积S．【答案】（1）平方米；（2）196平方米【分析】（1）利用长方形的面积公式及平行四边形的面积公式进行求解即可；（2）把相应的值代入（1）中运算即可．【详解】解：（1）由题意得：平方米；（2）当，，（平方米）．【点睛】本题主要考查多项式乘多项式，解答的关键是对相应的运算法则的掌握．十．两个乘法公式的基本运用（共7小题）33．已知是完全平方式，则m的值为 　   　．【答案】【分析】利用完全平方公式得到，从而得到，从而求出m值．【详解】解：∵是完全平方式，∴，∴，∴，故答案为：．【点睛】本题考查了完全平方式，解题的关键是熟练掌握完全平方公式．34．多项式是一个完全平方式，则k＝　   　．如果是完全平方式，则m的值是 　   　．【答案】16，【分析】利用完全平方公式的结构特征判断即可得解．【详解】解：∵多项式是一个完全平方式，∴，∵是完全平方式，∴，即，又∵，∴．故答案为：16，．【点睛】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．35．已知正方形的周长是cm，则其面积是 　   　cm2．【答案】【分析】先求得该正方形的边长，再运用完全平方公式进行求解．【详解】解：∵该正方形的边长为：（cm），∴该正方形的面积为：（cm2），故答案为：．【点睛】此题考查了完全平方公式的应用能力，关键是能准确理解并运用该知识．36．＝　   　．【答案】9【分析】原式变形后，利用完全平方公式化简，计算即可求出值．【详解】解：原式＝＝＝＝9．故答案为：9．【点睛】此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．37．运用乘法公式简便计算：＝　   　．【答案】1【分析】将数字适当变形后，利用平方差公式解答即可．【详解】解：原式＝＝＝＝1．故答案为：1．【点睛】本题主要考查了实数的运算，平方差公式，熟练掌握平方差公式是解题的关键．38．化简：．【答案】【分析】根据完全平方公式先把原式进行化简，再合并即可．【详解】解：＝＝．【点睛】本题考查了整式的混合运算，涉及的知识有：完全平方公式以及合并同类项法则，熟练掌握公式及法则是解本题的关键．39．阅读材料后解决问题．小明遇到下面一个问题：计算．经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：＝＝＝＝＝．请你根据小明解决问题的方法，试着解决以下的问题：（1）；（2）．【答案】（1）；（2）【分析】（1）根据题中例题可得，在本题式子前面可乘以，然后利用平方差公式即可算出答案；（2）根据题中例题可得，在整体的式子前面乘以，要想保持结果不变，再在式子前面乘以，然后利用平方差公式即可运算．【详解】解：（1）原式＝＝＝＝＝＝；（2）原式＝＝＝＝＝＝．【点睛】本题考查的是平方差公式的应用，解题关键是掌握平方差公式．十一．两个乘法公式的推广及综合运用（共7小题）40．如图，将图1的长方形用剪刀沿图中虚线（对称轴）剪开，分成四块形状和大小一样的小长方形，小长方形的长为a，宽为b（a＞b），再按图2的方式拼成一个正方形，通过拼接前后两个图形中阴影部分的面积关系可以验证的等式是（　　）A．B．C．D．【答案】B【分析】根据4个长方形的面积等于大正方形的面积减去小正方形的面积即可求解．【详解】解：∵图1阴影的面积为：，图2阴影的面积为：，∴，故选：B．【点睛】本题考查了完全平方公式与几何图形，数形结合是解题的关键．41．如图，对一个正方形进行了分割，通过面积恒等，能够验证下列哪个等式（　　）A．B．C．D．【答案】C【分析】观察图形的面积，从整体看怎么表示，再从分部分来看怎么表示，两者相等，即可得答案．【详解】解：首先看四个等式都是成立的，但是却并未都正确反映图示内容．图中大正方形的边长为：，其面积可以表示为：分部分来看：左下角正方形面积为，右上角正方形面积为，其余两个长方形的面积均为，各部分面积相加得：，∴故选：C．【点睛】本题考查了乘法公式的几何背景，明确几何图形面积的表达方式，熟练掌握相关乘法公式，是解题的关键．42．若，，则＝　   　．【答案】28【分析】先把变形为，然后把，代入计算即可．【详解】解：，当，时，原式＝．故答案为：28．【点睛】题考查了完全平方公式，掌握是解题的关键．43．已知，，则＝　   　．【答案】16【分析】将变形为，然后将，代入求解即可．【详解】.解：∵，，∴．故答案为：16．【点睛】本题主要考查了完全平方公式，掌握完全平方公式进行运算是关键．44．已知：，则＝　   　．【答案】7【分析】根据完全平方公式解答即可．【详解】解：∵，∴，∴，故答案为：7．【点睛】本题考查了完全平方公式，熟记完全平方公式是解题的关键．45．计算：＝　   　．【答案】【分析】原式利用完全平方公式展开即可得到结果．【详解】解：原式＝．故答案为：．【点睛】此题考查了完全平方公式，熟练掌握公式是解本题的关键．46．用如图所示的正方形和长方形卡片若干张，拼成一个边长为的正方形，需要B类卡片 　   　张．【答案】6【分析】根据题意列出关系式，利用完全平方公式化简即可作出判断．【解答】解：根据题意得：，则需要B类卡片6张．故答案为：6．【点评】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．十二．整式的混合运算（共3小题）47．计算：（1）；（2）．【答案】（1）；（2）【分析】（1）先去括号再合并同类项即可；（2）按照完全平方和公式和多项式除以单项式法则去括号，然后合并同类项即可．【详解】解：（1）原式＝；（2）原式＝＝＝．【点睛】本题考查了整式的计算，掌握完全平方和公式和相关运算法则是关键．48．计算：（1）；（2）．【答案】（1）；（2）【分析】（1）根据整式的乘除运算法则即可求出答案．（2）根据完全平方公式以及多项式乘多项式法则即可求出答案．【详解】解：（1）原式＝＝＝．（2）原式＝ ＝＝．【点睛】本题考查整式的混合运算，解题的关键是熟练运用整式的加减运算法则以及乘除运算法则，本题属于基础题型．49．规定一种新运算法则：．（1）求的值；（2）若，求的值．【答案】（1）3；（2）21【分析】（1）根据新定义的运算代入求解即可；（2）根据新定义的运算得出，然后代入求解即可．【详解】解：（1）由题意得：＝＝＝3；（2）由题意得：，解得：，∴＝＝＝21．【点睛】本题主要考查整式的混合运算，理解新定义的运算，熟练掌握运算法则是解题关键．十三．整式乘除的实际运用（共1小题）50．如图，两个形状大小相同的长方形和长方形，点E在边上，，，且a＞b＞0．（1）用含a，b的代数式分别表示和的面积；（2）当，．求图中阴影部分的面积． 【答案】（1）的面积为，的面积为；（2）20【分析】（1）根据已知易得，，从而可得 ，然后利用三角形的面积公式，进行计算即可解答；（2）根据阴影部分的面积＝梯形的面积﹣的面积﹣的面积，再利用（1）的结论，进行计算即可解答．【详解】解：（1）∵长方形和长方形是两个形状大小相同的长方形，∴，，∴，∴的面积＝；的面积＝，∴的面积为，的面积为；（2）∵，，∴阴影部分的面积＝梯形的面积﹣的面积﹣的面积＝＝＝＝＝＝＝＝20，∴图中阴影部分的面积为20．【点睛】本题考查了整式的混合运算，完全平方公式的几何背景，准确熟练地进行计算是解题的关键．