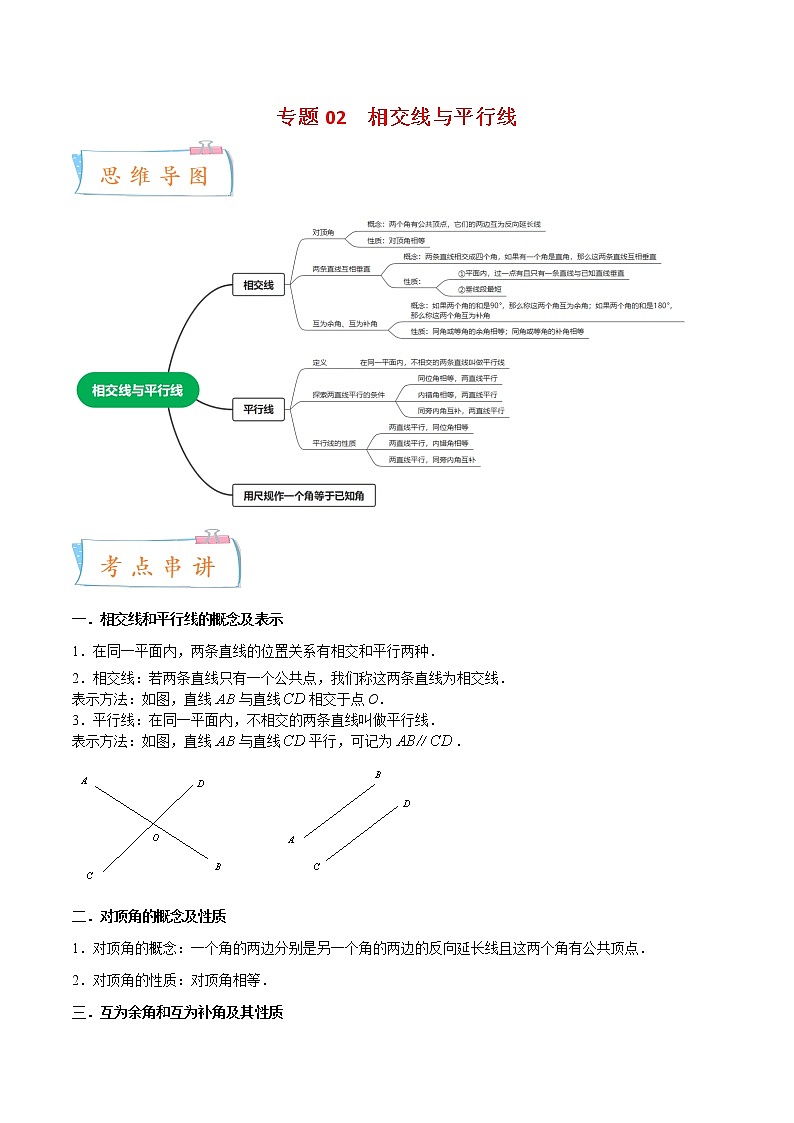
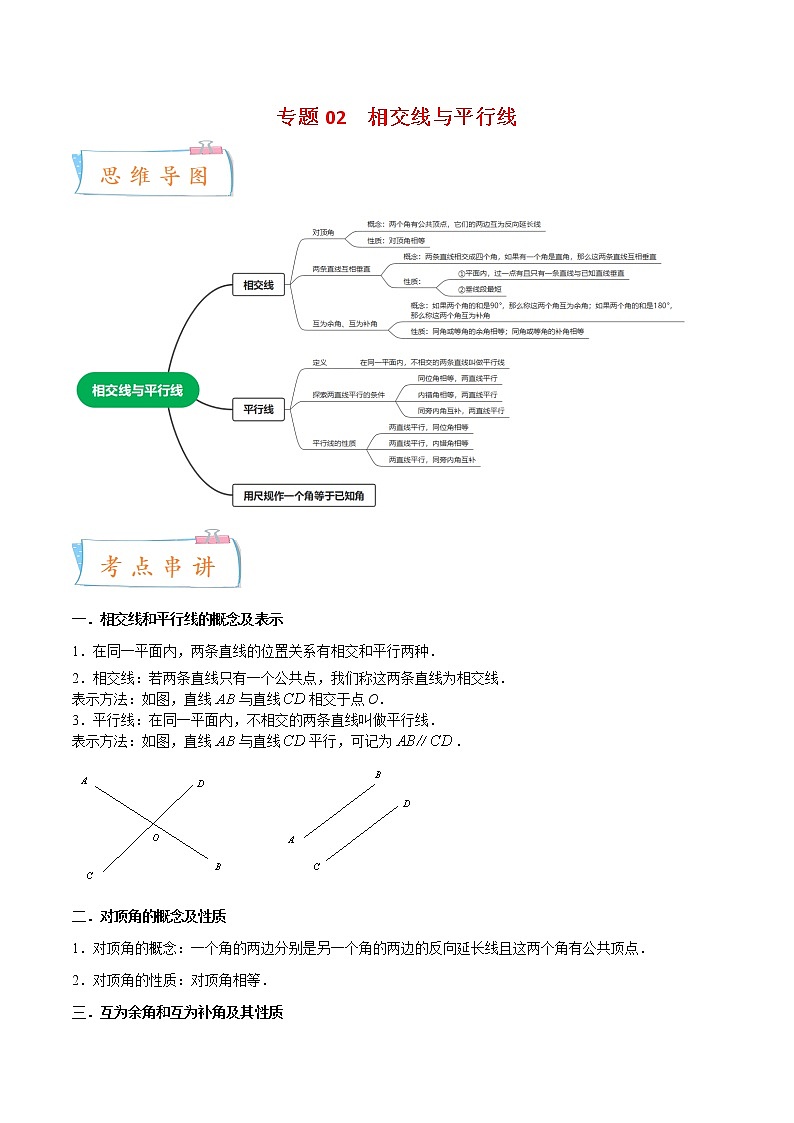
2022-2023年北师大版数学七年级下册专项复习精讲精练：专题02 相交线与平行线（11个考点）【考点串讲+热点题型专训】（原卷版+解析版）

专题02  相交线与平行线

一．相交线和平行线的概念及表示

1．在同一平面内，两条直线的位置关系有相交和平行两种．

2．相交线：若两条直线只有一个公共点，我们称这两条直线为相交线．

表示方法：如图，直线与直线相交于点O．

3．平行线：在同一平面内，不相交的两条直线叫做平行线．

表示方法：如图，直线与直线平行，可记为．

二．对顶角的概念及性质

1．对顶角的概念：一个角的两边分别是另一个角的两边的反向延长线且这两个角有公共顶点．

2．对顶角的性质：对顶角相等．

三．互为余角和互为补角及其性质

1．如果两个角的和是，那么称这两个角互为补角．

2．如果两个角的和是，那么称这两个角互为余角．

3．同角或等角的补角相等；同角或等角的余角相等．

四．垂直的概念及表示

1．两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足．

2．如图，直线与直线垂直，记作，点O是垂足．

五．垂线的性质

1．平面内，过一点有且只有一条直线与已知直线垂直．

2．直线外一点与直线上各点连接的所有线段中，垂线段最短．

六．点到直线的距离

1．过点A作直线l的垂线，垂足为点B，则线段的长度叫做点A到直线l的距离，此时线段叫垂线段．

七．探索直线平行的条件

1．同位角、内错角、同旁内角的概念

2．两条直线平行的条件：

①同位角相等，两直线平行；

②内错角相等，两直线平行；

③同旁内角互补，两直线平行．

3．过直线外一点有且只有一条直线与这条直线平行．

4．平行于同一条直线的两条直线平行．

八．平行线的性质

1．两直线平行，同位角相等．

2．两直线平行，内错角相等．

3．两直线平行，同旁内角互补．

九．利用尺规作一个角等于已知角

【专题过关】

一．对顶角及邻补角的概念及性质（共3小题）

1．下面四个图形中，与是邻补角的是（　　）

【答案】C

【分析】根据邻补角的定义，结合具体的图形进行判断即可．

【详解】解：根据邻补角的定义可知，

图中的与是邻补角，

故选：C．

【点睛】本题考查邻补角，理解邻补角的定义是正确解答的关键．

2．下列各图中，与是对顶角的是（　　）

【答案】C

【分析】根据对顶角的定义解答即可．

【详解】解：根据对顶角的定义可知：只有C选项中的是对顶角，其它都不是．

故选：C．

【点睛】本题考查对顶角的定义，掌握对顶角的定义是解题的关键．对顶角的定义：两条直线相交后所得

的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．

3．如图，直线和交于点O，平分，若，则的度数为（　　）

【答案】A

【分析】根据对顶角和邻补角的定义即可得到的度数，再根据角平分线即可得出的度数．

【详解】解：∵，

∴，

∴，

又∵平分，

∴．

故答案为：A．

【点睛】本题考查了邻补角、对顶角．解题的关键是掌握邻补角、对顶角的定义和性质，要注意运用：对顶角相等，邻补角互补，即和为．

二．余角与补角相关角度计算（共4题）

4．已知的余角为，则的补角度数是（　　）

【答案】B

【分析】根据余角的定义得出，再由补角的定义即可求出答案．

【详解】解：∵的余角为，

∴，

∴的补角．

故选：B．

【点睛】本题考查余角和补角的计算，掌握余角和补角的定义是解题关键．

5．若一个角的补角是这个角的余角的4倍，则这个角是（　　）

【答案】C

【分析】根据互为余角的两个角的和等于，互为补角的两个角的和等于，列出方程，然后解方程即可．

【详解】解：设这个角为，则它的补角为，余角为，

根据题意可得：，

解得：，

即这个角为，

故选：C．

【点睛】本题考查了互为余角与补角的性质，表示出这个角的余角与补角然后列出方程是解题的关键．

6．如图，被平分，且与互余，则的度数是（　　）

【答案】A

【分析】根据且与互余，得出，根据被平分，求出结果即可．

【解答】解：∵且与互余，

∴，

∵被平分，

∴．

故选：A．

【点睛】本题主要考查了余角的计算，角平分线的定义，解题的关键是根据余角的定义求出．

7．若与互补，且，则下列表示的余角的式子中：①；②；③

； ④．正确的是（　　）

【答案】B

【分析】根据和为的两个角互为余角即可求解．

【详解】解：∵与互补，

∴，

∴，

∴的余角为，则①符合题意；

∵＝＝＝，则②符合题意；

∵，则③不符合题意；

∵＝＝＝，④符合题意；

∴符合题意的有：①②④，

故选：B．

【点睛】本题主要考查了余角和补角以及角的概念，掌握角的概念以及余角和补角的定义是解题的关键．

三．垂线的相关概念（共3题）

8．下列四个说法：①两点确定一条直线；②过直线上一点有且只有一条直线垂直于已知直线；③连接直线

外一点与直线上各点的所有线段中，垂线段最短；④从直线外一点到这条直线的垂线段，叫做点到直线的

距离，其中正确的说法的个数是（　　）

【答案】B

【分析】根据两点确定一条直线，垂线的性质，垂线段最短，点到直线的距离的定义，逐项分析即可求解．

【详解】解：①两点确定一条直线，正确，符合题意；

②同一平面内，过直线上一点有且只有一条直线垂直于已知直线，不正确，不符合题意；

③连接直线外一点与直线上各点的所有线段中，垂线段最短，正确，符合题意；

④从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不正确，不符合题意．

故选：B．

【点睛】本题考查了两点确定一条直线，垂线的性质，垂线段最短，点到直线的距离的定义，掌握以上知

识是解题的关键．

9．点P为直线外一点，点A、B、C为直线上三点，，，，则P

到直线的距离为（　　）

【答案】D

【分析】直线外一点到直线的垂线段的长度，叫做点到直线的距离，由此即可判断．

【详解】解：由垂线的性质：垂线段最短，2＜4＜5，当时，点P到直线l的距离为2cm，当与l不垂直时，点P到直线l的距离小于2cm，

因此点P到直线l的距离小于或等于2cm即不大于2cm．

故选：D．

【点睛】本题考查点到直线的距离的概念，关键是掌握点到直线的距离的定义．

10．如图，，，垂足分别为C，D．则点A到直线的距离是线段 　   　的长．

【答案】

【分析】根据点到直线的距离是直线外的点到直线的垂线段的长度，可得答案．

【详解】解：，垂足为点C，，垂足为点D，则点A到的距离是线段的长度，

故答案为：．

【点睛】本题考查了点到直线的距离，点到直线的距离是直线外的点到直线的垂线段的长度．

四．垂线的性质应用（共3题）

11．如图，要把河中的水引到水池A中，应在河岸B处（），开始挖渠才能使水渠的长度最短，

这样做的依据是（　　）

【答案】C

【分析】根据垂线段的性质：垂线段最短进行解答．

【详解】解：要把河中的水引到水池A中，应在河岸B处（），开始挖渠才能使水渠的长度最短，这样做的依据是：垂线段最短，

故选：C．

【点睛】此题主要考查了垂线段的性质，垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它

是相对于这点与直线上其他各点的连线而言．

12．下列生活实例中，数学原理解释错误的是（　　）

【答案】D

【分析】由直线的性质：两点确定一条直线；线段的性质：两点之间，线段最短；垂线的性质：垂线段最短，即可判断．

【详解】解：A、测量两棵树之间的距离，要拉直皮尺，应用的数学原理是：两点之间，线段最短，正确，故A不符合题意；

B、用两颗钉子就可以把一根木条固定在墙上，应用的数学原理是：两点确定一条直线，正确，故B不符合题意；

C、测量跳远成绩，应用的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短，正确，故C不符合题意；

D、从一条河向一个村庄引一条最短的水渠，应用的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短，故D符合题意．

故选：D．

【点睛】本题考查直线的性质，线段的性质，垂线的性质，掌握以上知识点是解题的关键．

13．在体育课上某同学跳远的情况如图所示，直线l表示起跳线，经测量，米，米，

米，则该同学的实际立定跳远成绩是 　   　米．

【答案】3.1

【分析】根据垂线段的性质：垂线段最短，进行解答即可．

【详解】解：∵，

∴该同学的实际立定跳远成绩应测量图中线段的长，

∴该同学的实际立定跳远成绩为3.1米，

故答案为：3.1．

【点睛】此题主要考查了垂线段的性质，垂线段最短指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．

五．利用垂直的定义、对顶角性质等求角的度数（共2题）

14．如图，点O在直线上，已知，，则的度数为 　   　．

【答案】

【分析】先利用平角定义求出的度数，然后再根据垂直定义可得，从而利用角的和差关系，进行计算即可解答．

【详解】解：∵，

∴，

∵，

∴，

∴，

故答案为：．

【点睛】本题考查了垂线，根据题目的已知条件并结合图形进行分析是解题的关键．

15．如图，直线与直线相交于点O，，且平分，若，则

的度数为 　   　．

【答案】

【分析】根据邻补角的定义，由，得．根据角平分线的定义，由平分，得．再根据对顶角相等，得．根据垂直的定义，由，得，那么，进而推断出．

【详解】解：∵，

∴．

∵平分，

∴．

∴．

∵，

∴．

∴．

∴．

故答案为：．

【点睛】本题主要考查垂直、角平分线的定义、对顶角与邻补角，熟练掌握垂直的定义、角平分线的定义、对顶角与邻补角的定义是解决本题的关键．

六．同位角、内错角、同旁内角的识别（共3题）

16．下列图形中，和是同位角的是（　　）

【答案】A

【分析】根据同位角的概念求解即可．

【详解】解：A选项中和是同位角，

故选：A．

【点睛】本题主要考查同位角，两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．

17．如图，直线a，b被直线c所截，下列说法中不正确的是（　　）

【答案】C

【分析】根据同位角、内错角、同旁内角的定义进行判断即可．

【详解】解：A．与是对顶角，正确，因此选项A不符合题意；

B．与是直线a、直线b被直线c所截得的同位角，正确，因此选项B不符合题意；

C．与不是同旁内角，不正确，因此选项C符合题意；

D．与是直线a、直线b被直线c所截得的内错角，正确，因此选项D不符合题意；

故选：C．

【点睛】本题考查同位角、内错角、同旁内角以及对顶角、邻补角，理解同位角、内错角、同旁内角以及

对顶角的定义是正确判断的前提．

18．如图，下列说法正确的是（　　）

【答案】B

【分析】根据同位角、内错角、同旁内角的定义结合图形进行判断即可．

【详解】解：A．和不是同位角，原说法错误，故此选项不符合题意；

B．和是内错角，原说法正确，故此选项符合题意；

C．和是邻补角，原说法错误，故此选项不符合题意；

D．和不是同旁内角，原说法错误，故此选项不符合题意；

故选：B．

【点睛】本题考查同位角、内错角、同旁内角，理解同位角、内错角、同旁内角的定义是正确判断的前提．

七．平行线的判定（共4小题）

19．如图，下列能判定的条件有（　　）

①；

②；

③；

④．

【答案】B

【分析】根据平行线的判定定理判断求解即可．

【详解】解：∵，

∴，

故A符合题意；

由，不能判定，

故B不符合题意；

∵，

∴，

故C不符合题意；

∵，

∴，

故D符合题意；

故选：B．

【点睛】此题考查了平行线的判定，熟记平行线的判定定理是解题的关键．

20．如图表示钉在一起的木条a，b，c．若测得，，要使木条，木条a至少要旋

转 　   　°．

【答案】25

【分析】根据同位角相等两直线平行，求出旋转后的同位角的度数，然后用减去即可得到木条a旋转的度数．

【详解】解：如图，

∵时，，

∴要使木条a与b平行，木条a旋转的度数至少是．

故答案是：25．

【点睛】本题考查了平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．

21．阅读下面的解答过程，并填空．

如图，，平分，平分，．求证：．

证明：∵平分，平分，（已知）

∴　   　，　   　.（角平分线的定义）

又∵，（已知）

∴　   　＝　   　.（等量代换）

又∵，（已知）

∴　   　＝　   　.（等量代换）

∴．（ 　   　）

【答案】见解析

【分析】根据题意和图形，可以在证明过程中写入相应的条件，本题得以解决．

【详解】证明：∵平分，平分，（已知）

∴，．（角平分线的定义）

又∵，（已知）

∴．（等量代换）

又∵，（已知）

∴．（等量代换）

∴．（同位角相等，两直线平行）

故答案为：；；；；；；同位角相等，两直线平行．

【点睛】本题考查平行线的判定，解答本题的关键是明确题意，利用数形结合的思想解答．

22．如图，点E、F分别是、上的点，连接、、、，分别交、于点G、

H，若，，求证：．

【答案】见解析

【分析】根据平行线的判定和性质进行解答即可．

【详解】证明：∵，，

∴，

∴，

∴，

∵，

∴，

∴．

【点睛】本题主要考查了平行线的判定和性质，对顶角相等，熟练掌握同位角相等两直线平行，和内错角相等两直线平行，是解题的关键．

八．平行线判定的实际运用（共2小题）

23．如图，一个弯形管道，若它的两个拐角，，则管道．这

里用到的推理依据是 　   　．

【答案】同旁内角互补，两直线平行

【分析】由已知，，即，根据同旁内角互补，两直线平行即可得到．

【详解】解：∵，

∴，

∴（同旁内角互补，两直线平行），

故答案为：同旁内角互补，两直线平行．

【点睛】本题考查的是平行线的判定，解答本题的关键是掌握平行线的判定定理：同旁内角互补，两直线平行．

24．《七彩云南》少数民族传统艺术表演，是七彩云南欢乐世界的王牌演艺节目，它荟萃云南人文之美，深

受观众喜爱．在展演中，舞台上的灯光由灯带上位于点A和点C的两盏激光灯控制．如图，光线与灯

带的夹角，当光线与灯带的夹角　   　时，．

【答案】或

【分析】根据平行线的判定定理求解即可．

【详解】解：当在的右侧时，时，，理由如下：

∵，，

∴，

∴，

当在的左侧时，时，，

故答案为：或．

【点睛】此题考查了平行线的判定，熟记“同旁内角互补，两直线平行”是解题的关键．

九．利用平行线的性质求角的度数（共5小题）

25．如图，直线、被直线所截，已知，，则的度数为（　　）

【答案】C

【分析】先根据对顶角相等得出的度数，然后根据平行线的性质得出的度数即可．

【详解】解：如图，

∵，

∴，

∵，

∴．

故选：C．

【点睛】本题考查了平行线的性质，掌握两直线平行，同位角相等是解题的关键．

26．如图，一条公路修到湖边时，需拐弯绕湖而过，在A，B，C三处经过三次拐弯，此时道路恰好和第一

次拐弯之前的道路平行（即），若，，则的度数是 　   　．

【答案】

【分析】首先过B作，根据，可得，进而得到，，然后可求出的度数．

【详解】解：如图所示，过B作，

∵，

∴，

又∵，

∴，

∵，

∴，

∴，

故答案为：

【点睛】此题主要考查了平行线性质，关键是掌握两直线平行，同旁内角互补；两直线平行，内错角相等．

27．如图1，将一条两边互相平行的纸条折叠．

（1）若图中，则　   　°．

（2）在图1的基础上继续折叠，使得图1中的边与边重合（如图2），若继续沿边折叠，边恰好平分，则此时的度数为 　   　度．

【答案】（1）50；45

【分析】（1）根据两直线平行，同位角相等，可知，再利用折叠的性质可知；

（2）根据折叠的性质可知，折叠两次后形成的三个角与折叠后的都相等，而这四个角的和为，故每个角为，从而可知，再由（1）的思路可得的值．

【详解】解：（1）根据上下边互相平行可知，，

∵，

∴．

又，

∴．

故答案为：50．

（2）根据折叠的性质可知，折叠两次后形成的三个角都相等，

根据题意可知，折叠两次后形成的三个角与折叠后的都相等，而这四个角的和为，故每个角为，

∴，即，

由（1）中可得，．

故答案为：45．

【点睛】本题考查学生对平行线性质和折叠问题的掌握情况，根据实际情况对问题进行解答．学生可以自

主动手操作，通过实际操作可以较容易的对问题进行解答．

28．如图，已知，，平分，，求和的度数．

【答案】；

【分析】平分，，根据角平分线的性质，即可求得的度数，又由，根据两直线平行，内错角相等，即可求得的度数，根据两直线平行，同旁内角互补，即可求得的度数，即可求得的度数．

【详解】解：∵，平分，

∴，

∵，

∴，，

∵，

∴，

∴．

∴，．

【点睛】此题考查了平行线的性质与角平分线的定义，掌握两直线平行，内错角相等与两直线平行，同旁内角互补定理的应用是解此题的关键．

29．把一块含角的直角三角尺（，）放在两条平行线，之间．

（1）如图1，若三角形的角的顶点G放在上，且，求的度数；

（2）如图2，若把三角尺的两个锐角的顶点E，G分别放在和上，请你探索并说明与间的数量关系；

（3）如图3，若把三角尺的直角顶点F放在上，角的顶点E落在上，请直接写出与的数量关系．

【答案】（1）；（2）；（3）

【分析】（1）依据，可得，再根据，，即可得出，进而得到；

（2）根据，可得，再根据，即可得到；

（3）依据，可知，再代入，，即可求出．

【详解】解：（1）∵，

∴，

∵，

∴，

又∵，

∴，

∴；

（2）∵，

∴，

即，

又∵，

∴；

（3）．理由如下：

∵，

∴，

∴，

∵，，

∴，

∴．

【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是掌握：两直线平行，同旁内角互补．

十．平行线的判定与性质的综合运用（共2小题）

30．在下列解答中，填上适当的数式或理由：

如图，，平分，试说明：．

解：∵（ 　   　），

∴　   　（ 　   　），

∵平分（已知），

∴　   　（ 　   　），

∵（已知），

∴　   　（ 　   　）．

∴　   　（等量代换）

即．

【答案】见解析

【分析】利用平行线的性质，角平分线的定义即可求解．

【详解】解：∵（已知），

∴（两直线平行，内错角相等），

∵平分（已知），

∴（角平分线的定义），

∵（已知），

∴（两直线平行，内错角相等）．

∴（等量代换）

即．

故答案为：已知；C；两直线平行，内错角相等；；角平分线的定义；E；两直线平行，内错角相等；E．

【点睛】本题考查了平行线的性质，角平分线的定义．熟记各图形的性质并准确识图是解题的关键．

31．如图所示，，，．

（1）求证：．

（2）若，求的度数．

【答案】见解析

【分析】（1）根据平行线的性质与判定可得，根据题意，即可得证；

（2）由（1）得，根据三角形内角和定理可得，根据，即可求解．

【详解】（1）证明：∵，

∴，

又∵，

∴，

∴，

又∵，

∴；

（2）解：由（1）得，

∵，

∴，，

∵，

∴．

【点睛】本题考查了平行线的性质与判定，三角形内角和定理，掌握平行线的性质与判定是解题的关键．

十一．平行线相关动角问题（共1小题）

32．如图1，，，，求度数．

小明的思路是：过P作，如图2，通过平行线性质来求．

（1）按小明的思路，易求得的度数为 　   　；请说明理由；

（2）如图3，，点P在射线上运动，当点P在A、B两点之间运动时，，，则、、之间有何数量关系？请说明理由；

（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出、、间的数量关系．

【答案】（1）；（2）；（3）见解析

【分析】（1）利用铅笔模型，进行计算即可解答；

（2）过点P作，然后利用猪脚模型，进行计算即可解答；

（3）分两种情况：当点P在射线上运动时；当点P在上运动时；分别进行推理，即可解答．

【详解】解：（1）∵，，

∴，

∵，

∴，

∴，

∴，

故答案为：；

（2），

理由：过点P作，

∴，

∵，

∴，

∴，

∵，

∴；

（3）分两种情况：

当点P在射线上运动时，，

理由：如图：过点P作，

∴，

∵，

∴，

∴，

∵，

∴；

当点P在上运动时，，

理由：如图：过点P作，

∴，

∵，

∴，

∴，

∵，

∴；

综上所述：当点P在射线上运动时，；当点P在上运动时，．

【点睛】本题考查了平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．