第9章中心对称图形–平行四边形单元测试（能力提升卷，八下苏科）- 2022-2023学年八年级数学下册 必刷题【苏科版】

2022-2023学年八年级数学下册 必刷题【苏科版】

第9章中心对称图形–平行四边形单元测试（能力提升卷，八下苏科）

班级：___________________   姓名：_________________   得分：_______________

注意事项：

本试卷满分100分，试题共24题，其中选择8道、填空8道、解答8道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．

一、选择题（本大题共8小题，每小题2分，共16分）在每小题所给出的四个选项中，只有一项是符合题目要求的．

1．（2023•崂山区一模）“中国结”是我国特有的手工编织工艺品，也是一种传统吉祥装饰物．下列四个中国结图案中，既是中心对称图形又是轴对称图形的有（　　）

A．1个 B．2个 C．3个 D．4个

【分析】根据中心对称图形与轴对称图形的概念进行判断即可．

【详解】解：左起第1、3、4这三个图形既是中心对称图形又是轴对称图形，

第二个图形是中心对称图形，不是轴对称图形，

故选：C．

2．（2023•海淀区校级开学）如图，△ABC绕点C按顺时针旋转30°到△DEC，若点A恰好在DE上，则∠BAC的度数为（　　）

A．15° B．55° C．65° D．75°

【分析】先根据旋转的性质得∠ACD＝30°，∠BAC＝∠D，再根据三角形外角性质得∠BAE+∠BAC＝∠D+∠ACD，所以∠BAE＝∠ACD＝30°．根据旋转的性质得CA＝CD，进而得∠D＝∠CAD，所以∠BAC＝∠CAD，进而求出∠BAC的度数．

【详解】解：∵△ABC绕点C按顺时针旋转30°到△DEC，

∴∠ACD＝30°，∠BAC＝∠D，

∵∠EAC＝∠D+∠ACD，

即∠BAE+∠BAC＝∠D+∠ACD，

∴∠BAE＝∠ACD＝30°．

∵CA＝CD，

∴∠BAC＝∠CAD，

∴∠BAC＝（180°﹣30°）÷2＝75°．

故选：D．

3．（2022秋•泰山区期末）如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　）

A．OA＝OC，OB＝OD B．AB＝CD，AO＝CO 

C．AB＝CD，AD＝BC D．∠BAD＝∠BCD，AB∥CD

【分析】由平行四边形的判定方法分别对各个选项进行判断即可．

【详解】解：A、∵OA＝OC，OB＝OD，

∴四边形ABCD是平行四边形，故选项A不符合题意；

B、由AB＝CD，AO＝CO不能判断四边形ABCD是平行四边形，故选项B符合题意；

C、∵AB＝CD，AD＝BC，

∴四边形ABCD是平行四边形，故选项C不符合题意；

D、∵AB∥CD，

∴∠ABC+∠BCD＝180°，

∵∠BAD＝∠BCD，

∴∠ABC+∠BAD＝180°，

∴AD∥BC，

∴四边形ABCD是平行四边形，故选项D不符合题意；

故选：B．

4．（2022秋•深圳期末）要检验一个四边形画框是否为矩形，可行的测量方法是（　　）

A．测量四边形画框的两个角是否为90° 

B．测量四边形画框的对角线是否相等且互相平分 

C．测量四边形画框的一组对边是否平行且相等 

D．测量四边形画框的四边是否相等

【分析】由平行四边形的判定与性质、菱形的判定，矩形的判定分别对各个选项进行判断即可．

【详解】解：A、测量四边形画框的两个角是否为90°，不能判定为矩形，故选项A不符合题意；

B、测量四边形画框的对角线是否相等且互相平分，能判定为矩形，故选项B符合题意；

C、测量四边形画框的一组对边是否平行且相等，能判定为平行四边形，不能判定是否为矩形，故选项C不符合题意；

D、测量四边形画框的四边是否相等，能判定为菱形，故选项D不符合题意；

故选：B．

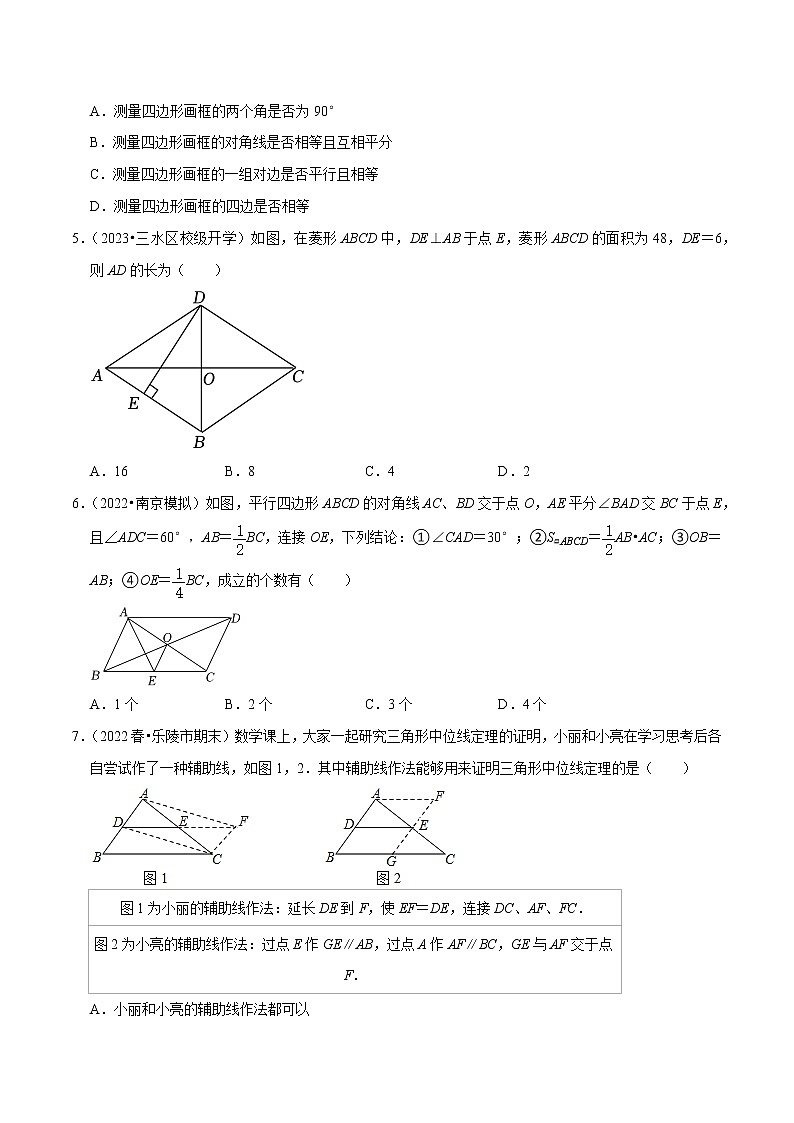
5．（2023•三水区校级开学）如图，在菱形ABCD中，DE⊥AB于点E，菱形ABCD的面积为48，DE＝6，则AD的长为（　　）

A．16 B．8 C．4 D．2

【分析】由菱形的性质得AD＝AB，再由菱形的面积求出AB＝8，即可得出结论．

【详解】解：∵四边形ABCD是菱形，

∴AD＝AB，

∵DE⊥AB，

∴菱形ABCD的面积＝AB•DE＝48，

即6AB＝48，

∴AB＝8，

∴AD＝AB＝8，

故选：B．

6．（2022•南京模拟）如图，平行四边形ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝BC，连接OE，下列结论：①∠CAD＝30°；②S▱ABCD＝AB•AC；③OB＝AB；④OE＝BC，成立的个数有（　　）

A．1个 B．2个 C．3个 D．4个

【分析】由平行四边形ABCD中，∠ADC＝60°，易得△ABE是等边三角形，又由，证得①∠CAD＝30°；继而证得AC⊥AB，得②S平行四边形ABCD＝AB⋅AC；可得OE是三角形的中位线，证得④．

【详解】解：∵四边形ABCD是平行四边形，

∴∠ABC＝∠ADC＝60°，∠BAD＝120°，

∵AE平分∠BAD，

∴∠BAE＝∠EAD＝60°

∴△ABE是等边三角形，

∴AE＝AB＝BE，

∵，

∴，

∴∠BAC＝90°，

∴∠CAD＝30°，故①正确；

∵AC⊥AB，

∴S平行四边形ABCD＝AB•AC，故②错误；

∵，，

∵BD＞BC，

∴AB≠OB，故③错误；

∵∠CAD＝30°，∠AEB＝60°，AD//BC，

∴∠EAC＝∠ACE＝30°，

∴AE＝CE，

∴BE＝CE，

∵OA＝OC，

∴，故④正确；

故选：B．

7．（2022春•乐陵市期末）数学课上，大家一起研究三角形中位线定理的证明，小丽和小亮在学习思考后各自尝试作了一种辅助线，如图1，2．其中辅助线作法能够用来证明三角形中位线定理的是（　　）

A．小丽和小亮的辅助线作法都可以 

B．小丽和小亮的辅助线作法都不可以 

C．小丽的辅助线作法可以，小亮的不可以 

D．小亮的辅助线作法可以，小丽的不可以

【分析】根据平行四边形的判定定理，用两种方法都可以证明三角形中位线定理，得到答案．

【详解】解：小丽的作法：∵AE＝EC，DE＝EF，

∴四边形ADCF为平行四边形，

∴CF＝AD，CF∥AD，

∵AD＝DB，

∴DB＝CF，

∴四边形DBCF为平行四边形，

∴DE＝BC，DE∥BC，能够用来证明三角形中位线定理；

小亮的作法：∵GE∥AB，AF∥BC，

∴四边形ABGF为平行四边形，

∴AB＝FG，AF＝BG，

∵DB＝AB，EG＝FG，

∴BD＝EG，

∴四边形DBGE为平行四边形，

∴DE＝BG，DE∥BG，

∵AF∥BC，

∴∠AFE＝∠CGE，

在△AEF和△CEG中，

，

∴△AEF≌△CEG（AAS），

∴AF＝GC，

∴BG＝GC，

∴DE＝BC，能够用来证明三角形中位线定理，

故选：A．

8．（2022秋•渠县校级期末）如图，E是边长为1的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（　　）

A． B． C． D．

【分析】连接AC，PB，AC交BD于O，根据S△BCE＝S△BPC+S△BPE，从而BE•OC＝BE•PR+，进一步得出结论．

【详解】解：如图，

连接AC，PB，AC交BD于O，

∵四边形ABCD是正方形，

∴AC⊥BD，AC＝BC＝，

∴OC＝AC＝，

∵S△BCE＝S△BPC+S△BPE，

∴BE•OC＝BE•PR+，

∵BC＝BE，

∴BE•OC＝BE•PR+BE•PQ，

∴PR+PQ＝OC＝，

故选：A．

二．填空题（共8小题）

9．（2022•丰顺县校级开学）如图，为估计池塘岸边A，B两点间的距离，在池塘的一侧选取点O，分别取OA，OB的中点M，N，测得MN＝32cm，则A，B两点间的距离是 　0.64　m．

【分析】根据三角形中位线定理解答即可．

【详解】解：∵点M，N分别为OA，OB的中点，

∴MN是△OAB的中位线，

∴AB＝2MN＝64cm＝0.64m，

故答案为：0.64．

10．（2022秋•新罗区校级月考）如图，△ABC与△AB'C'关于点A对称，若∠C＝90°，∠B＝30°，AC＝1，则BB'的长为 　4　．

【分析】利用全等三角形的性质证明AB＝AB′，利用直角三角形30度角的性质求出AB＝2，可得结论．

【详解】解：如图，

∵△ABC与△AB'C'关于点A对称，

∴△ABC≌△AB′C′，

∴AB＝AB′，

∵∠C＝90°，∠B＝30°，AC＝1，

∴AB＝2AC＝2，

∴BB′＝2AB＝4，

故答案为：4．

11．（2022秋•东港区校级月考）如图，菱形ABCD的对角线AC、BD交于点O，AC＝4，BD＝16，将△BOC绕着点C旋转180°得到△B'O'C，则点A与点B'之间的距离为 　10　．

【分析】根据菱形ABCD的对角线AC、BD交于点O，AC＝4，BD＝16，可得AC⊥BD，所以∠BOC＝90°，根据△BOC绕着点C旋转180°得到△B′O′C，所以∠CO′B′＝∠BOC＝90°，AO′＝6，OB′＝8，再根据勾股定理即可求出点A与点B′之间的距离．

【详解】解：∵菱形ABCD的对角线AC、BD交于点O，AC＝4，BD＝16，

∴AC⊥BD，

∴∠BOC＝90°，

∵△BOC绕着点C旋转180°得到△B′O′C，

∴∠CO′B′＝∠BOC＝90°，

∴O′C＝OC＝OA＝AC＝2，

∴AO′＝6，

∵OB＝OD＝O′B′＝BD＝8，

在Rt△AO′B′中，根据勾股定理，得

AB′＝＝＝10．

则点A与点B′之间的距离为10．

故答案为：10．

12．如图，在▱ABCD中，AC与BD相交于点O，点E是BC边上一点，AC是∠DAE的平分线，若AE＝5，AO＝4，则△AEC的面积为 　12　．

【分析】先证△AEC是等腰三角形，再由勾股定理求出OE的长，即可得出答案．

【详解】解：连接EO，如图所示：

∵四边形ABCD是平行四边形，

∴∠DAC＝∠BCA，AO＝CO，

∴AC＝2AO＝2×4＝8，

∵AC是∠DAE的平分线，

∴∠DAC＝∠EAC，

∴∠EAC＝∠ECA，

∴AE＝CE，

∴EO⊥AC，

在Rt△AOE中，由勾股定理得：OE＝＝＝3，

∴S△AEC＝AC•OE＝×8×3＝12，

故答案为：12．

13．（2022秋•泰山区校级期末）在平行四边形ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB＝6，EF＝2，则BC的长为 　10或14　．

【分析】根据平行四边形的性质可得CD＝AB＝6，结合角平分线的定义，等腰三角形的性质可求解AF＝AB＝6，DE＝DC＝6，由EF＝2即可求得BC的长．

【详解】解：∵四边形ABCD为平行四边形，AB＝6，

∴CD＝AB＝6，AD∥BC，

∴∠AFB＝∠CBF，

∵BF平分∠ABC，

∴∠ABF＝∠CBF，

∴∠ABF＝∠AFB，

∴AF＝AB＝6，

同理DE＝DC＝6，

如图1，∵EF＝2，

∴AE＝AF﹣EF＝6﹣2＝4，

∴AD＝BC＝AE+DE＝4+6＝10，

如图2，∵EF＝2，

∴AE＝AF+EF＝6+2＝8，

∴AD＝BC＝AE+DE＝6+8＝14，

综上所述，BC的长为10或14，

故答案为：10或14．

14．（2022秋•锦江区期末）小颖将能够活动的菱形学具活动成为图1所示形状，并测得AC＝5，∠B＝60°，接着，她又将这个学具活动成为图2所示正方形，此时A'C'的长为 　5　．

【分析】根据菱形的性质得出AB＝BC，求出△ABC是等边三角形，根据等边三角形的性质得出AB＝BC＝AC＝5，根据旋转的性质得出A′B′＝B′C′＝AB＝5，再根据勾股定理求出A′C′即可．

【详解】解：∵四边形ABCD是菱形，

∴AB＝BC，

∵∠B＝60°，

∴△ABC是等边三角形，

∴AB＝BC＝AC，

∵AC＝5，

∴AB＝BC＝5，

∵四边形A′B′C′D′为正方形，

∴∠A′B′C′＝90°，

由旋转的性质得出A′B′＝B′C′＝AB＝5，

∴A′C′＝＝5，

故答案为：5．

15．（2022秋•朝阳区校级期末）如图，Rt△ABC中，∠ACB＝90°，∠B＝30°，．点D为边AB上一个动点，作DE⊥BC、DF⊥AC，垂足为E、F，连结EF．则EF长度的最小值为 　　．

【分析】解直角三角形求出AC和AB，求出四边形CFDE是矩形，根据矩形的性质得出CD＝EF，当CD⊥AB时，CD有最小值，此时EF有最小值，根据三角形的面积公式求出CD长几颗．

【详解】解：∵∠ACB＝90°，∠B＝30°，，

∴AC＝＝2，AB＝2AC＝4，

连接CD，

∵DF⊥AC，∠ACB＝90°，DE⊥BC，

∴∠DFC＝∠FCE＝∠DEC＝90°，

∴四边形CFDE是矩形，

∴EF＝CD，

当CD⊥AB时，CD长最小，此时EF有最小值，

∵S△ACB＝＝，

∴＝CD，

∴CD＝，

∴EF长度的最小值是，

故答案为：．

16．（2022•南京模拟）如图，正方形ABCD的边长为6．E，F分别是射线AB，AD上的点（不与点A重合），且EC⊥CF，M为EF的中点．P为线段AD上一点，AP＝1，连接PM．当△PMF为直角三角形时，则AE的长为 　或10　．

【分析】分当∠PMF＝90°，当∠MPF＝90°两种情况讨论，根据正方形的性质，勾股定理即可求解．

【详解】解：如图1所示，当∠PMF＝90°时，

∵四边形ABCD是正方形，

∴∠CBE＝∠CDF＝90°，BC＝DC，

∵∠BCD＝∠ECF＝90°，

∴∠BCD＝∠DCF

∴△CBE≌△CDF（ASA），

∴BE＝DF，

∵EM＝MF，PM⊥EF，

∴PE＝PF，

设AE＝x，则BE＝DF＝6﹣x，

∵PA＝1，

∴PE＝PF＝5+6﹣x＝11﹣x，

在Rt△PAE中，∵PE2＝AE2+PA2，

∴（11﹣x）2＝x2+12，

∴x＝，

∴AE＝．

如图2所示，当∠MPF＝90°．连接AM，

∵∠A＝∠MPF＝90°，

∴MP∥AE，

∴MP⊥AF

∵ME＝MF，

∴MA＝MF

∴PA＝PF＝1，

∴DF＝BE＝4，

∴AE＝AB+BE＝10，

综上所述，AE的值为或10．

三．解答题（共8小题）

17．（2022春•历城区期末）如图，正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求解答下列问题：

（1）△A1B1C1与△ABC关于坐标原点O成中心对称，则B1的坐标为 　（2，2）　．

（2）△A1B1C1的面积为 　2.5　．

（3）将△ABC绕某点逆时针旋转90°后，其对应点分别为A2（﹣1，﹣2），B2（1，﹣3），C2（0，﹣5），则旋转中心的坐标为 　（0，﹣1）　．

【分析】（1）根据关于原点成中心对称的点的特征求救；

（2）利用割补法求三角形的面积；

（3）利用作图观察求解．

【详解】解：（1）∵B（﹣2，﹣2），

∴B1（2，2）．

故答案为：（2，2）．

（2）△A1B1C1的面积为：××＝2.5

故答案为：2.5．

（3）根据旋转的性质，旋转中心在对称点的连线的垂直平分线上，所以两对对称点的垂直平分线的交点就是旋转中心．

所以旋转中心的坐标为：（0，﹣1）．

故答案为：（0，﹣1）．

18．（2022秋•二道区校级期末）图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法，保留作图痕迹．

（1）在图①中画个轴对称四边形ABCD，使其面积为17．

（2）在图②中画出一个中心对称图形ABEF，使其面积为17．

（3）在图③中画出一个四边形ABMN，使其满足仅有一对对角都为直角．

【分析】（1）作出边长为的正方形即可；

（2）作出底为3，高为4的平行四边形即可；

（3）作出∠ABM＝∠BAN＝90°的四边形即可．

【详解】解：（1）如图，四边形ABGH即为所求．

（2）如图，四边形CDMN即为所求．

（3）如图，四边形EFPQ即为所求．

19．（2021秋•宝塔区校级期末）如图，△ABC中，AB＝AC，BE⊥AC于E，且D、E分别是AB、AC的中点，延长BC至点F，使CF＝CE，连接DE，EF．

（1）求∠ABC的度数；

（2）若DE＝2，求△CEF的面积．

【分析】（1）证明△ABC是等边三角形，可得结论；

（2）过E点作EG⊥BC，求出EG，CF可得结论．

【详解】解：（1）：BE⊥AC于E，E是AC的中点，

∴AB＝BC．

∵AB＝AC，

∴AB＝BC＝AC，

∴△ABC是等边三角形，

∴∠ABC＝60°；

（2）如图，过E点作EG⊥BC，

∵D、E分别是AB、AC的中点，DE＝2

∴BC＝2DE＝4，

∵BE⊥AC，

∴∠EBC＝∠ABC＝30°，

∴CE＝2＝CF，BE＝＝2，

∴EG＝BE＝，

∴S△ECF＝×CF×EG＝×2×＝．

20．（2022春•立山区校级月考）已知：如图，在▱ABCD中，对角线AC，BD交于点O，AB⊥AC，AB＝2，BC＝．

（1）求平行四边形ABCD的面积S▱ABCD；

（2）求对角线BD的长．

【分析】（1）先根据勾股定理求出AC的长，再根据S▱ABCD＝2S△ABC即可得出结论；

（2）根据AC的长得出OA的长，由勾股定理求出OB的长，进而可得出结论．

【详解】解：（1）∵AB⊥AC，AB＝2，BC＝，

∴AC＝＝＝3，

∴S▱ABCD＝2S△ABC＝2××2×3＝6；

（2）∵AC＝3，

∴OA＝AC＝，

∴OB＝＝＝，

∴BD＝2OB＝5．

21．（2022秋•安徽期末）如图，在四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．线段CD绕点C顺时针旋转60°得到线段CE，连接AE，DE．

（1）求证：∠BCD＝∠ACE；

（2）若∠ADC＝30°，AD＝6，BD＝10，求DE的长．

【分析】（1）结合旋转的性质和等边三角形的性质可知∠ACB＝∠DCE＝60°，然后可知∠ACB+∠ACD＝∠DCE+∠ACD，即可证明∠BCD＝∠ACE；

（2）利用“SAS”证明△BCD≌△ACE，可得AE＝BD＝10，再结合等边三角形的性质可推导∠ADE＝90°，在Rt△ADE中由勾股定理即可获得答案．

【详解】（1）证明：由旋转可知∠DCE＝60°，CD＝CE，

∵△ABC是等边三角形，

∴∠ACB＝60°，AC＝BC，

∴∠ACB＝∠DCE＝60°，

∴∠ACB+∠ACD＝∠DCE+∠ACD，即∠BCD＝∠ACE；

（2）解：在△BCD和△ACE中，

，

∴△BCD≌△ACE（SAS），

∴AE＝BD＝10，

∵∠DCE＝60°，CD＝CE，

∴△CDE是等边三角形，

∴∠CDE＝60°，

又∵∠ADC＝30°，

∴∠ADE＝∠ADC+∠CDE＝90°，

在Rt△ADE中，．

22．（2022春•西峰区校级月考）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF＝DC；

（2）若AB＝AC，试判断四边形ADCF的形状，并证明你的结论．

【分析】（1）根据平行线的性质得出∠AFE＝∠DBE，根据AAS证明△AFE≌△DBE，推出AF＝BD，即可得出答案；

（2）证得四边形ABDF是平行四边形，得到AB＝DF，进而证得AC＝DF，再证得四边形ADCF是平行四边形，即可得到四边形ADCF是矩形．

【详解】（1）证明：∵E是AD的中点，

∴AE＝DE，

∵AF∥BC，

∴∠AFE＝∠DBE．

在△AFE和△DBE中，

，

∴△AFE≌△DBE（AAS），

∴AF＝DB．

∵AD是BC边上的中线，

∴DC＝DB，

∴AF＝DC；

（2）解：四边形ADCF是矩形．

证明：连接DF，

由（1）得AF＝DB，AF∥DB，

∴四边形ABDF是平行四边形，

∴AB＝DF，

∵AB＝AC，

∴AC＝DF，

由（1）得AF＝DC，AF∥DC，

∴四边形ADCF是平行四边形，

∴四边形ADCF是矩形．

23．（2022秋•峰峰矿区校级期末）如图，▱ABCD中，AB＝3cm，BC＝5cm，∠B＝60°，点G是CD的中点，点E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．

（1）求证：四边形CEDF是平行四边形；

（2）①直接写出：当AE＝　1.5　cm时，四边形CEDF是菱形（不需要说明理由）；

②当AE＝　3.5　cm时，四边形CEDF是矩形，请说明理由．

【分析】（1）证△CFG≌△EDG，推出FG＝EG，根据平行四边形的判定推出即可；

（2）①证△CDE是等边三角形，推出CE＝DE，再根据菱形的判定推出即可．

②求出△MBA≌△EDC，推出∠CED＝∠AMB＝90°，再根据矩形的判定推出即可．

【详解】（1）证明：∵四边形ABCD是平行四边形，

∴BC∥AD，

∴∠FCG＝∠EDG，

∵G是CD的中点，

∴CG＝DG，

在△CFG和△DEG中，

，

∴△CFG和△DEG（ASA），

∴FG＝EG，

又∵CG＝DG，

∴四边形CEDF是平行四边形．

（2）解：①当AE＝2cm时，四边形CEDF是菱形，理由如下：

∵四边形ABCD是平行四边形，

∴AD＝5cm，CD＝AB＝3cm，∠CDE＝∠B＝60°，

∵AE＝2cm，

∴DE＝AD﹣AE＝3cm，

∴DE＝CD，

∴△CDE是等边三角形，

∴CE＝DE，

∵四边形CEDF是平行四边形，

∴平行四边形CEDF是菱形，

②当AE＝3.5时，平行四边形CEDF是矩形，理由如下：

如图，过A作AM⊥BC于M，

∵∠B＝60°，AB＝3cm，

∴BM＝AB＝1.5cm，

∵AE＝3.5cm，

∴DE＝AD﹣AE＝1.5cm＝BM，

在△MBA和△EDC中，

，

∴△MBA≌△EDC（SAS），

∴∠CED＝∠AMB＝90°，

∵四边形CEDF是平行四边形，

∴平行四边形CEDF是矩形，

故答案为：3.5．

24．（2022春•南谯区校级月考）如图1，四边形ABCD为正方形，E为对角线AC上一点，连接DE，BE．

（1）求证：BE＝DE；

（2）如图2，过点E作EF⊥DE，交边BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．

①求证：矩形DEFG是正方形；

②若正方形ABCD的边长为9，CG＝3，求正方形DEFG的边长．

【分析】（1）根据正方形的性质证明△ABE≌△ADE（SAS），即可解决问题；

（2）①作EM⊥BC于M，EN⊥CD于N，得到EN＝EM，然后证得∠DEN＝∠FEM，得到△DEN≌△FEM，则有DE＝EF，根据正方形的判定即可证得矩形DEFG是正方形；

②证明△ADE≌△CDG（SAS），可得AE＝CG，∠DAE＝∠DCG＝45°，证明CE⊥CG，连接EG，根据勾股定理即可解决问题．

【详解】（1）证明：∵四边形ABCD为正方形，

∴∠BAE＝∠DAE＝45°，AB＝AD，

在△ABE和△ADE中，

，

∴△ABE≌△ADE（SAS），

∴BE＝DE；

（2）①证明：如图，作EM⊥BC于M，EN⊥CD于N，

得矩形EMCN，

∴∠MEN＝90°，

∵点E是正方形ABCD对角线上的点，

∴EM＝EN，

∵∠DEF＝90°，

∴∠DEN＝∠MEF＝90°﹣∠FEN，

∵∠DNE＝∠FME＝90°，

在△DEN和△FEM中，

，

∴△DEN≌△FEM（ASA），

∴EF＝DE，

∵四边形DEFG是矩形，

∴矩形DEFG是正方形；

②解：∵正方形DEFG和正方形ABCD，

∴DE＝DG，AD＝DC，

∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，

∴∠CDG＝∠ADE，

在△ADE和△CDG中，

，

∴△ADE≌△CDG（SAS），

∴AE＝CG，∠DAE＝∠DCG＝45°，

∵∠ACD＝45°，

∴∠ACG＝∠ACD+∠DCG＝90°，

∴CE⊥CG，

∴CE+CG＝CE+AE＝AC＝AB＝9．

∵CG＝3，

∴CE＝6，

连接EG，

∴EG＝＝＝3，

∴DE＝EG＝3．

∴正方形DEFG的边长为3．