中考数学总复习四点共圆模型难点解析与训练

这是一份中考数学总复习四点共圆模型难点解析与训练，共8页。
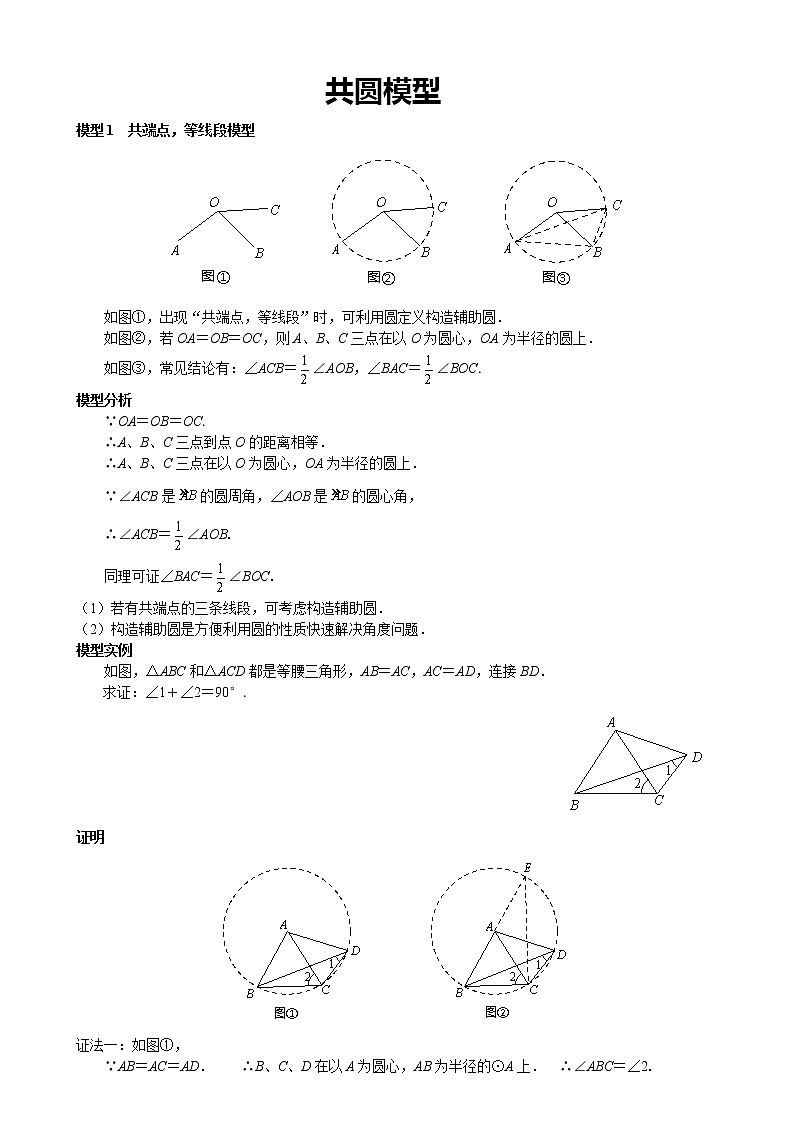
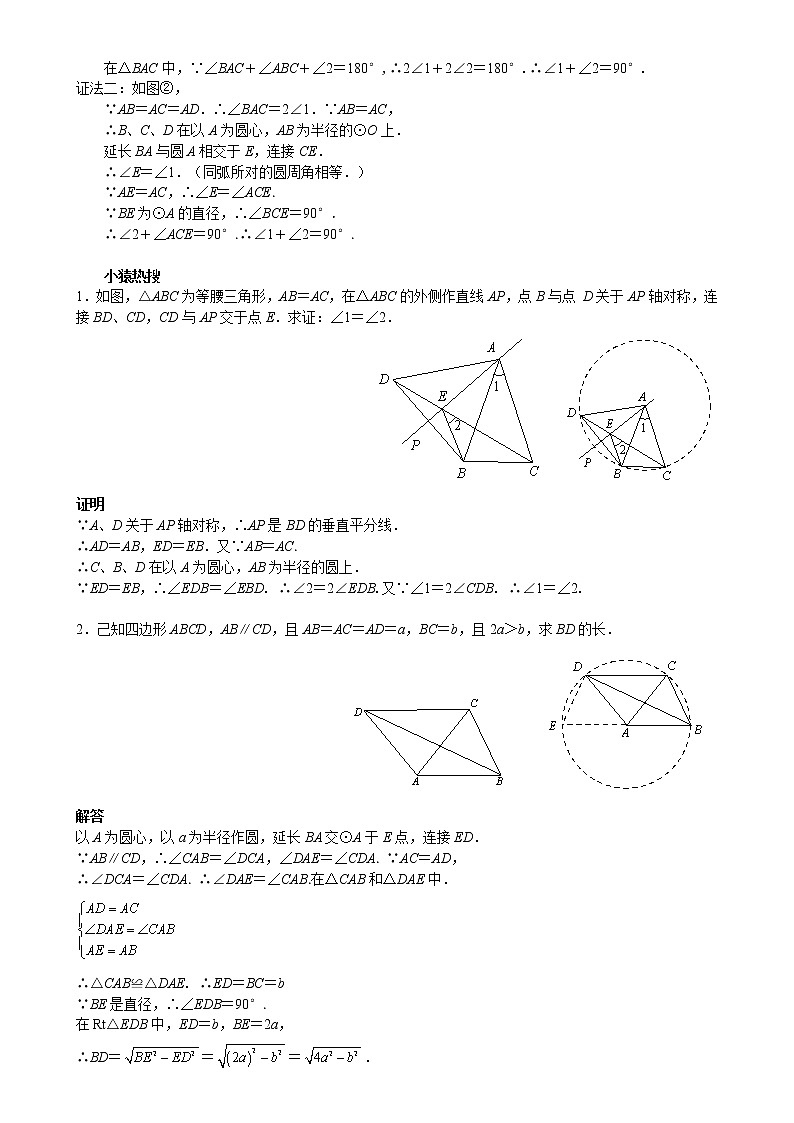
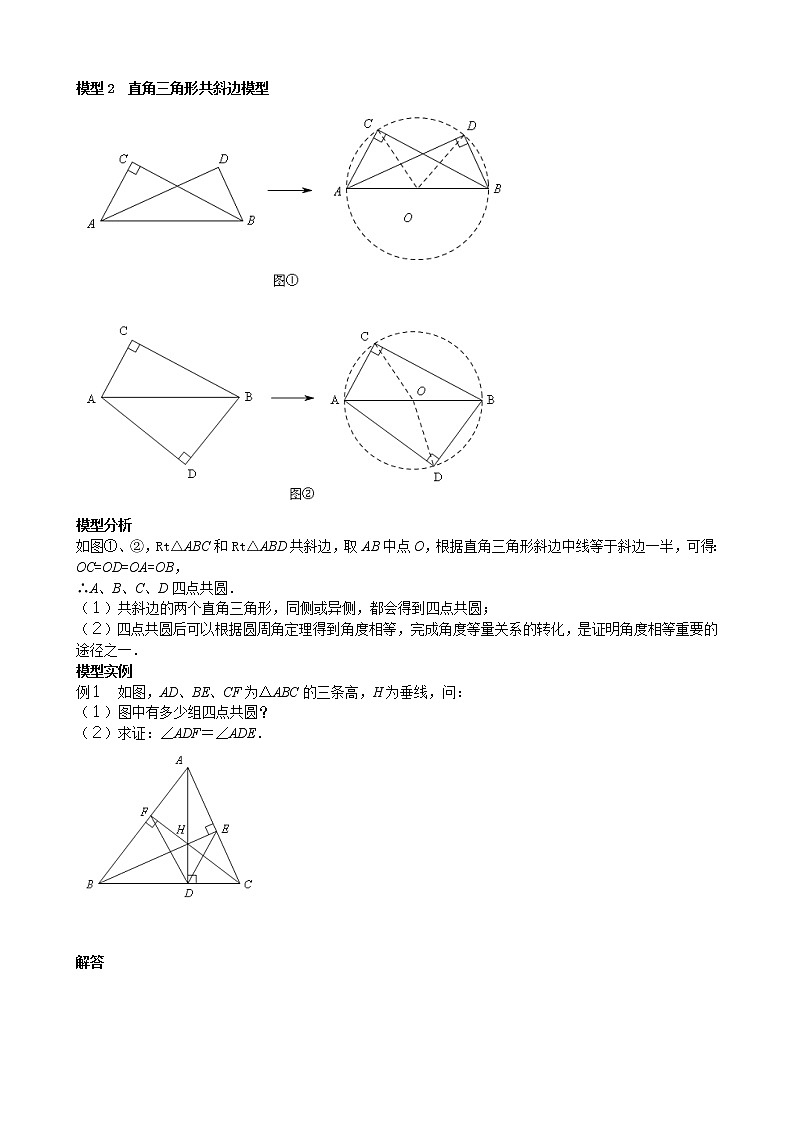
共圆模型模型1  共端点，等线段模型       如图①，出现“共端点，等线段”时，可利用圆定义构造辅助圆．如图②，若OA＝OB＝OC，则A、B、C三点在以O为圆心，OA为半径的圆上．如图③，常见结论有：∠ACB＝∠AOB，∠BAC＝∠BOC.模型分析∵OA＝OB＝OC.∴A、B、C三点到点O的距离相等．∴A、B、C三点在以O为圆心，OA为半径的圆上．∵∠ACB是的圆周角，∠AOB是的圆心角，∴∠ACB＝∠AOB.同理可证∠BAC＝∠BOC.（1）若有共端点的三条线段，可考虑构造辅助圆．（2）构造辅助圆是方便利用圆的性质快速解决角度问题．模型实例    如图，△ABC和△ACD都是等腰三角形，AB＝AC，AC＝AD，连接BD．求证：∠1＋∠2＝90°.  证明       证法一：如图①，∵AB＝AC＝AD．　　∴B、C、D在以A为圆心，AB为半径的⊙A上．　∴∠ABC＝∠2.在△BAC中，∵∠BAC＋∠ABC＋∠2＝180°,∴2∠1＋2∠2＝180°.∴∠1＋∠2＝90°.证法二：如图②，∵AB＝AC＝AD．∴∠BAC＝2∠1．∵AB＝AC，∴B、C、D在以A为圆心，AB为半径的⊙O上．延长BA与圆A相交于E，连接CE．∴∠E＝∠1．（同弧所对的圆周角相等．）∵AE＝AC，∴∠E＝∠ACE.∵BE为⊙A的直径，∴∠BCE＝90°．∴∠2＋∠ACE＝90°.∴∠1＋∠2＝90°.  小猿热搜1．如图，△ABC为等腰三角形，AB＝AC，在△ABC的外侧作直线AP，点B与点 D关于AP轴对称，连接BD、CD，CD与AP交于点E．求证：∠1＝∠2．证明∵A、D关于AP轴对称，∴AP是BD的垂直平分线．∴AD＝AB，ED＝EB．又∵AB＝AC.∴C、B、D在以A为圆心，AB为半径的圆上．∵ED＝EB，∴∠EDB＝∠EBD. ∴∠2＝2∠EDB.又∵∠1＝2∠CDB. ∴∠1＝∠2. 2．己知四边形ABCD，AB∥CD，且AB＝AC＝AD＝a，BC＝b，且2a＞b，求BD的长．   解答以A为圆心，以a为半径作圆，延长BA交⊙A于E点，连接ED．∵AB∥CD，∴∠CAB＝∠DCA，∠DAE＝∠CDA. ∵AC＝AD，∴∠DCA＝∠CDA. ∴∠DAE＝∠CAB.在△CAB和△DAE中．∴△CAB≌△DAE. ∴ED＝BC＝b∵BE是直径，∴∠EDB＝90°.在Rt△EDB中，ED＝b，BE＝2a，∴BD＝＝＝． 模型2  直角三角形共斜边模型模型分析如图①、②，Rt△ABC和Rt△ABD共斜边，取AB中点O，根据直角三角形斜边中线等于斜边一半，可得：OC=OD=OA=OB，∴A、B、C、D四点共圆．（１）共斜边的两个直角三角形，同侧或异侧，都会得到四点共圆；（２）四点共圆后可以根据圆周角定理得到角度相等，完成角度等量关系的转化，是证明角度相等重要的途径之一．模型实例例１　如图，AD、BE、CF为△ABC的三条高，H为垂线，问：（１）图中有多少组四点共圆？（２）求证：∠ADF＝∠ADE．  解答（１）６组①C、D、H、E四点共圆，圆心在CH的中点处；②D、B、F、H四点共圆，圆心在BH的中点处；③A、E、H、F四点共圆，圆心在AH的中点处；④C、B、F、E四点共圆，圆心在BC的中点处；⑤B、A、E、D四点共圆，圆心在AB的中点处；⑥C、D、F、A四点共圆，圆心在AC的中点处．（２）如图，由B、D、H、F四点共圆，得∠ADF=∠1. 同理：由A、B、D、E四点共圆，得∠ADE=∠１.∴∠ADF＝∠ADE． 例２　　如图，E是正方形ABCD的边AB上的一点，过点E作DE的垂线交∠ABC的外角平分线于点F，求证：FE=DE. 解答如图，连接DB、DF. ∵四边形ABCD是正方形，且BF是∠CBA的外角平分线，∴∠CBF=45°，∠DBC=45°， ∴∠DBF=90°．又∵∠DEF=90°，∴D、E、B、F四点共圆．∴∠DFE=∠DBE=45°（同弧所对的圆周角相等）．∴△DEF是等腰直角三角形．∴FE=DE．  1.如图，锐角△ABC中，BC.CE是高线，DG⊥CE于G，EF⊥BD于F，求证： 证明：由于Rt△BCE与Rt△BCD共斜边BC，∴B、C、D、E四点共圆．∴∠DBC=∠DEG，同理，Rt∠EDF与Rt△DGE共斜边DE，∴D、E、F、G四点共圆．于是∠DEG=∠DFG，因此，∠DBC=∠DFG．于是FG∥BC   2. 如图， BE.CF为△ABC的高，且交于点H,连接AH并延长交于BC于点D,求证：AD⊥BC.                3.如图，等边△PQR内接于正方形ABCD,其中点P,Q,R分别在边AD,AB,DC上，M是QR的中点.求证：不论等边△PQR怎样运动，点M为不动点.    4.如图，已知△ABC中，AH是高，AT是角平分线，且TD⊥AB,TE⊥AC.求证：∠AHD=∠AHE.   证明：（1）∵∠ADT=∠AHT=∠AET=90°，
∴D，E，H在以AT为直径的圆上，
∴∠AHD=∠ATD，∠AHE=∠ATE，
又∵AT是角平分线，TD⊥AB，TE⊥AC，
∴∠ATD=∠ATE，
∴∠AHD=∠AHE．  补充：  】