初中数学北师大版八年级下册3 线段的垂直平分线课后复习题

北师大版八年级数学下册 1.3线段的垂直平分线课后强化

 班级：________      姓名：________

一、单选题（共 10 小题）

1、如图，Rt△ABC中，∠C＝90°，∠B＝30°，分别以点A和点B为圆心，大于的长为半径作弧，两弧相交于M、N两点，作直线MN，交BC于点D，连接AD，则∠CAD的度数是(     )

A．20° B．30° C．45° D．60°

2、如图，已知，以两点为圆心，大于的长为半径画圆，两弧相交于点，连接与相较于点，则的周长为（    ）

A．8 B．10 C．11 D．13

3、如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（　　）

A．4cm B．3cm C．2cm D．1cm

4、如图，已知△ABC，∠ACB＝90°，BC＝3，AC＝4，小红按如下步骤作图：

①分别以A、C为圆心，以大于AC的长为半径在AC两边作弧，交于两点M、N；

②连接MN，分别交AB、AC于点D、O；

③过C作CEAB交MN于点E，连接AE、CD．

则四边形ADCE的周长为（　　）

A．10 B．20 C．12 D．24

5、观察下列作图痕迹，所作CD为△ABC的边AB上的中线是（　　）

A． B．

C． D．

6、如图，在△ABC中AB＝AC，BC＝8，面积是20，AC的垂直平分线EF分别交AC、AB边于E、F点，若点D为BC边的中点，点M为线段上一动点，则△CDM周长的最小值为（　　）

A．8 B．9 C．10 D．12

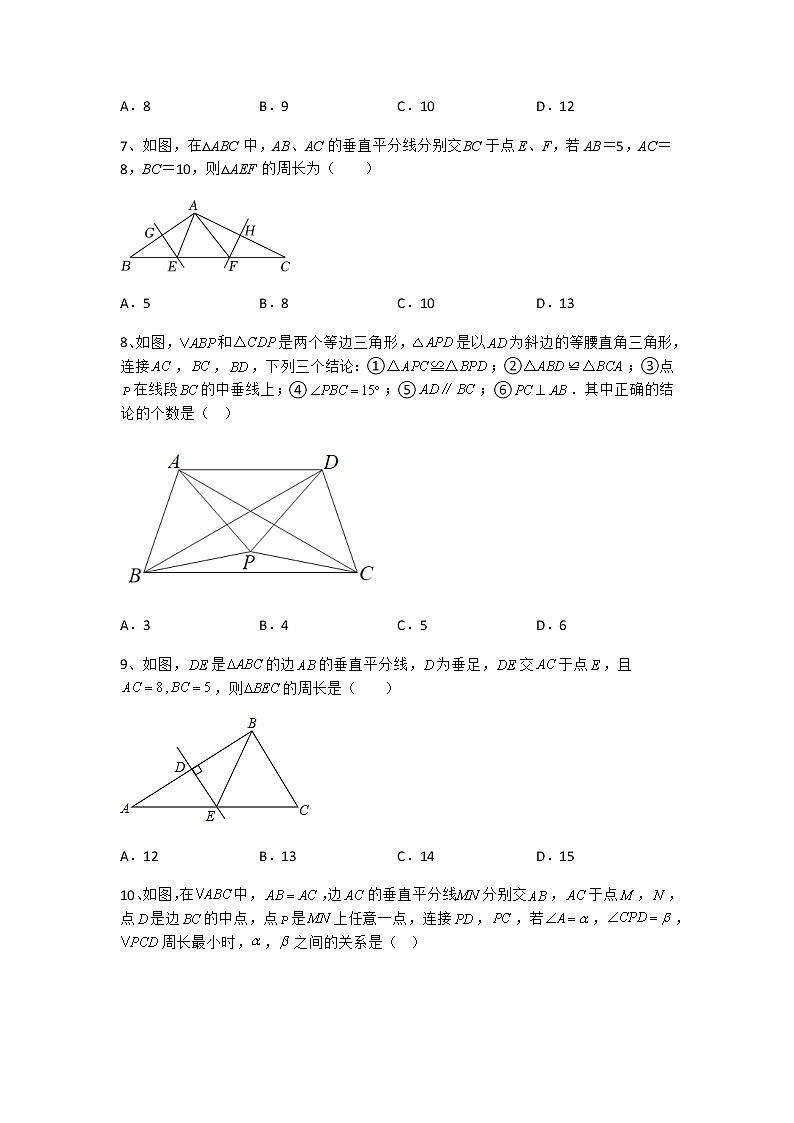
7、如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若AB＝5，AC＝8，BC＝10，则△AEF的周长为（　　）

A．5 B．8 C．10 D．13

8、如图，和是两个等边三角形，是以为斜边的等腰直角三角形，连接，，，下列三个结论：①；②；③点在线段的中垂线上；④；⑤；⑥．其中正确的结论的个数是（    ）

A．3 B．4 C．5 D．6

9、如图，是的边的垂直平分线，为垂足，交于点，且，则的周长是（　　）

A．12 B．13 C．14 D．15

10、如图，在中，，边的垂直平分线分别交，于点，，点是边的中点，点是上任意一点，连接，，若，，周长最小时，，之间的关系是（    ）

A． B． C． D．

二、填空题（共 8 小题）

1、在△ABC中，AB＝AC，点D是△ABC内一点，点E是CD的中点，连接AE，作EF⊥AE，若点F在BD的垂直平分线上，∠BAC＝α，则∠BFD＝_________．（用α含的式子表示）

2、如图，在四边形ABCD中，．在BC，CD上分别找一点M，N，使周长最小，则的度数为_________．

3、内部有一点P，，点P关于的对称点为M，点P关于的对称点为N，若，则的面积为_______．

4、如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，D为BC边上的中点，腰AB的垂直平分线EF交AD于M，交AC于点F，则BM+DM的值为_____cm．

5、如图，在中，，分别以点为圆心，大于的长为半径画弧，两弧相交于点作直线，交边于点，连接，则的周长为________．

6、如图，在△ABC中，点F是边AB、AC的中垂线的交点，联结BF、CF，如果∠BFC＝110°，那么∠A＝______°．

7、如图，垂直平分，垂直平分，若，则__________°．

8、如图，∠A＝52°，O是AB，AC的垂直平分线的交点，则∠OCB＝___________．

三、解答题（共 6 小题）

1、如图，在中，AB的垂直平分线EF交BC于点E，交AB于点F，点D为线段CE的中点，，．求证：．

2、观察图片中的风筝，它们的主体部分可以看成是一个四边形，这类四边形的特征是两组邻边分别相等，我们把这样的四边形叫做“筝形”．

(1)提出猜想：通过观察、测量等方法猜想筝形的对角线有什么性质，写出你的猜想______．（写出一个即可）

(2)证明猜想．（结合图1写出已知，求证，并证明）．

(3)解决问题．如图2，在筝形ABCD中，∠DAB＝60°，∠ABC＝∠ADC＝90°，AB＝AD＝6，求对角线AC的长．

3、如图，在中，，．

(1)在线段上找到一个点，使得．（尺规作图，不写作法，保留作图痕迹）．

(2)在（1）的条件下，连接，求证：是等边三角形．

4、如图，有点A、B、C、D，请用无刻度直尺和圆规画出一点P，使PA＝PB且PC＝PD（不写作法，请把作图痕迹用黑水笔描清楚）．

5、某班举行文艺晚会，桌子摆成两条直线（），桌面上摆满了橘子，桌面上摆满了糖果，坐在C处的小明先拿橘子再拿糖果，然后回到座位，请你帮他设计路线，使其行走的总路程最短．（保留作图痕迹）

6、如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD＝DE．

（1）若∠BAE＝40°，求∠C的度数；

（2）若△ABC周长为20cm，AC＝8cm，求DC长．

-参考答案-

一、单选题

1、B

【详解】在△ABC中，∵∠B=30°，∠C=90°，

∴∠BAC=180°-∠B-∠C=60°，

由作图可知MN为AB的中垂线，

∴DA=DB，

∴∠DAB=∠B=30°，

∴∠CAD=∠BAC-∠DAB=30°，

故选B．

2、A

【详解】由作法得MN垂直平分AB，

∴DA=DB，

∴△BDC的周长=DB+DC+BC=DA+DC+BC=AC+BC=5+3=8．

故选A．

3、C

【详解】连接AM，AN，

∵AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F，

∴BM=AM，CN=AN，

∴∠MAB=∠B，∠CAN=∠C，

∵∠BAC=120°，AB=AC，

∴∠B=∠C=30°，

∴∠BAM+∠CAN=60°，∠AMN=∠ANM=60°，

∴△AMN是等边三角形，

∴AM=AN=MN，

∴BM=MN=NC，

∵BC=6，

∴MN=2．

故选：C．

4、A

【详解】：∵分别以A、C为圆心，以大于AC的长为半径在AC两边作弧，交于两点M、N，

∴MN是AC的垂直平分线，

∴AD=CD，AE=CE，

∴∠CAD=∠ACD，∠CAE=∠ACE，

∵CEAB，

∴∠CAD=∠ACE，

∴∠ACD=∠CAE，

∴CDAE，

∴四边形ADCE是平行四边形，

∴四边形ADCE是菱形；

∴OA=OC=AC=2，OD=OE，AC⊥DE，

∵∠ACB=90°，

∴DEBC，

∴OD是△ABC的中位线，

∴OD=BC=×3=1.5，

∴AD==2.5，

∴菱形ADCE的周长=4AD=10．

故选A．

5、B

【详解】作AB边的垂直平分线，交AB于点D，连接CD，

∴点D即为线段AB的中点，

∴CD为△ABC的边AB上的中线．

故选：B．

6、B

【详解】如图所示，连接AD，AM，

∵是等腰三角形，点D是BC边的中点，

∴，

，

解得：，

∵EF是线段AC的垂直平分线，

∴点C关于直线EF的对称点为点A，

∴，

∵，

∴的长为的最小值，

∴的周长最短=．

故选：B．

7、C

【详解】∵EG是线段AB的垂直平分线，

∴EA＝EB，

同理，FA＝FC，

∴△AEF的周长＝EA＋EF＋FA＝EB＋EF＋FC＝BC＝10，

故选：C．

8、C

【详解】∵△ABP和△CDP是两个等边三角形，△APD是以AD为斜边的等腰直角三角形，

∴PA＝PB＝PD＝PC，∠APB＝∠DPC＝∠PAB＝∠PDC＝60°，∠APD＝90°，∠PAD＝∠PDA＝45°，

∴∠APC＝∠BPD＝150°，

在△APC和△BPD中，

，

∴△APC≌△BPD（SAS），所以①正确；

∵PB＝PC，

∴点P在线段BC的中垂线上，所以③正确；

∵∠BPA＝∠CPD＝60°，∠APD＝90°，

∴∠BPC＝150°，

∵PB＝PC，

∴∠PBC＝15°，所以④正确；

∵∠ABC＝60°＋15°＝75°，∠BAD＝∠PAB＋∠PAD＝60°＋45°＝105°，BD＝AC，

∴∠ABC≠∠BAD，

∴△ABD与△BCA不全等，所以②错误；

∵∠ABC＋∠BAD＝75°＋105°＝180°，

∴AD∥BC，所以⑤正确；

延长CP交AB于H，如图，

∵∠PCB＝15°，∠ABC＝75°，

∴∠ABC＋∠PCB＝90°，

∴∠CHB＝90°，

∴PC⊥AB，所以⑥正确．

正确的有5个，

故选：C．

9、B

【详解】∵是的边的垂直平分线，

∴，

∵，

∴的周长是：．

故选B．

10、C

【详解】如图，连接AP，

∵直线MN是线段AC的垂直平分线，且P在线段MN上，

∴PA=PC，．

∵,

∴．

由图可知CD为定值，当A、P、D在同一直线上时，最小，即为的长，

∴此时最小．

∵D是边BC的中点，AB=AC，

∴AD为的平分线，

∴．

∵，即，

∴．

故选C．

二、填空题

1、180°﹣α．

【详解】延长AE至M，使EM＝AE，

连接AF，FM，DM，

∵点E是CD的中点，

∴DE＝CE，

在△AEC与△MED中，

，

∴△AEC≌△MED（SAS），

∴∠EAC＝∠EMD，AC＝DM，

∵EF⊥AE，

∴AF＝FM，

∵点F在BD的垂直平分线上，

∴FB＝FD，

在△MDF与△ABF中，

，

∴△MDF≌△ABF（SSS），

∴∠AFB＝∠MFD，∠DMF＝∠BAF，

∴∠BFD+∠DFA＝∠DFA+∠AFM，

∴∠BFD＝∠AFM

＝180°﹣2（∠DMF+∠EMD）

＝180°﹣（∠FAM+∠BAF+∠EAC）

＝180°﹣∠BAC

＝180°﹣α，

故答案为：180°﹣α．

2、160°

【详解】

作点A关于BC和CD的对称点，连接，交BC于M，交CD于N，

则即为周长最小值

，

故答案为：160°．

3、

【详解】如图，根据题意得，OA垂直平分PM，OB垂直平分PN，

∴∠MOA=∠AOP，∠NOB=∠BOP，OM=OP=ON=5，

∴∠MON=2∠AOB=90°，

∴△MON的面积=OMON=×5×5=．

故答案为．

4、6．

【详解】∵△ABC是等腰三角形，点D是BC边的中点，

∴AD⊥BC，

∴S△ABC＝BC•AD＝×4×AD＝12，

解得AD＝6（cm），

∵EF是线段AB的垂直平分线，

∴AM＝BM，

∴BM+MD＝AM+DM＝AD＝6（cm），

故答案为：6．

5、

【详解】∵在中，分别以A、B为圆心，大于的长为半径画弧，两弧交于M，N，作直线MN，交BC边于D，连接AD；

∴MN为AB的垂直平分线，

∴AD=BD，

∴的周长为：AD+DC+AC=BC+AC=13；

故答案为13.

6、55

【详解】连接并延长至点，

点是边、的中垂线的交点，

，，

，，

，，

，

故答案为：55．

7、

【详解】∵在△ABC中，∠BAC=110°，

∴∠B+∠C=180°﹣110°=70°，

∵垂直平分，垂直平分，

∴AD=BD，AE=CE，

∴∠B=∠BAD，∠C=∠CAE，

∴∠BAD+∠CAE=70°，

∴∠ADE=∠BAC﹣（∠BAD+∠CAE）=110°﹣70°=40°，

故答案为：40°．

8、38°

【详解】∵O是AB、AC的垂直平分线的交点，

∴点O是△ABC的外心．

如图，连接OB．

则∠BOC=2∠A=104°．

又∵OB=OC，

∴∠OBC=∠OCB．

∴∠OCB=（180°-∠BOC）÷2=38°，

故答案是：38°．

三、解答题

1、见解析

【详解】证明：连接AE，

∵，，

∴，

∴．

∵点D为线段CE的中点，

∴，

∴AD垂直平分线段CE，

∴，

∵EF垂直平分AB，

∴，

∴．

2、(1)AC⊥BD

(2)见解析

(3)

【详解】（1）

解：通过观察和测量可知AC⊥BD，BD垂直平分AC，

故答案为∶AC⊥BD．

（2）

解：已知：如图1所示，AD=CD，AB=BC．

求证∶AC⊥BD．

证明∶

在△ABD和△CBD中，

∴△ABD≌△CBD(SSS)，

∴∠ADO=∠CDO，

在△AOD和△COD中，

∴△ADO≌△CDO(SAS)，

∴∠AOD=∠COD，

∵∠AOD+∠COD=180°

∴2∠AOD=180°．

∠AOD=90°

∴AC⊥BD．

（3）

解：∵四边形ABCD为筝行，

∴AB=AD，BC=DC，

∶∠ABC=∠ADC=90°，

在Rt△ABC和Rt△ADC中，

∴Rt△ABC≌Rt△ADC(HL)，

∴∠BAC=∠DAC，

∵∠BAD=60°，

∴∠BAC=∠BAD=60°=30°

∴BC=AC，

设BC=x，则AC=2x，

在Rt△ABC中，

∴

解得x=BC= ，

∴AC= ．

3、(1)见解析；

(2)见解析

【详解】（1）

解：如图所示：

（2）

∵∠BAC＝90°，∠C＝30°

∴∠B＝60°，

又∵点D在AC的垂直平分线上，

∴DA＝DC，

∴∠CAD＝∠C＝30°，

∴∠DAB＝60°，

∴∠ADB＝∠B＝∠DAB＝60°，

即△ABD是等边三角形．

4、作图见解析

【详解】如图所示，点P即为所求：

5、见解析

【详解】如图所示，小明的行走路线为，此时所走的总路程为的长，总路程最短．

6、（1）∠C＝35°；（2）DC＝6cm．

【详解】（1）∵EF垂直平分AC，

∴AE＝EC，

∴∠C＝∠CAE，

∵AD⊥BC，BD＝DE，

∴AD垂直平分BE，

∴AB＝AE，

∴∠ABE=∠AED，

∵∠BAE＝40°，

∴∠AED＝ ，

∴∠C∠AED＝35°；

（2）∵△ABC周长20cm，AC＝8cm，

∴AB+BE+EC＝12cm，

即2DE+2EC＝12cm，

∴DE+EC＝DC＝6cm．