2023年九年级数学中考复习专题 反比例函数中的面积问题课件

这是一份2023年九年级数学中考复习专题 反比例函数中的面积问题课件，共23页。PPT课件主要包含了方法1分割法，方法2补形法，例题图①，例题图②，例题图③，例题图④，第1题图，第1题解图，1求k与m的值，第2题图等内容，欢迎下载使用。
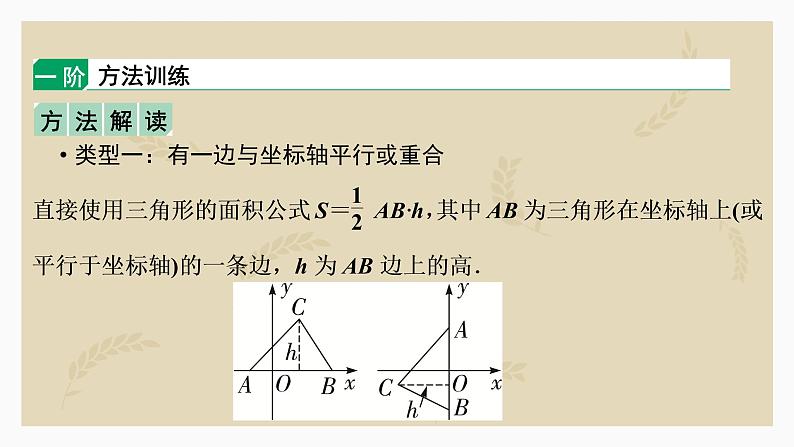
类型一：有一边与坐标轴平行或重合
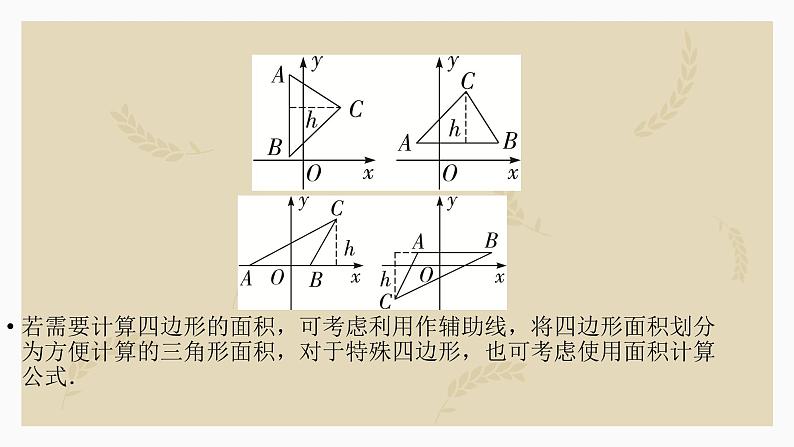
若需要计算四边形的面积，可考虑利用作辅助线，将四边形面积划分为方便计算的三角形面积，对于特殊四边形，也可考虑使用面积计算公式．
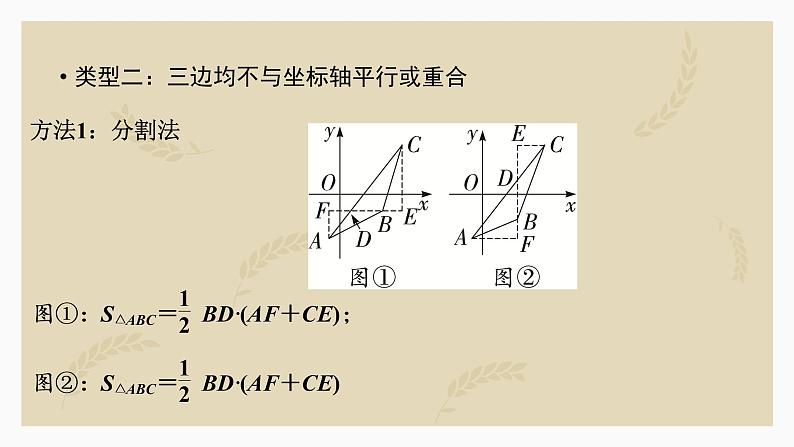
类型二：三边均不与坐标轴平行或重合
图③：S△ABC＝S△AFC－S△AEF－S△ABE－S△BEC；图④：S△ABC＝S△AEC－S△ABE－S△BEC
(1)如图①，若AB⊥x轴，△AOB的面积为3，求反比例函数的解析式；
(2)如图②，四边形OCDB是矩形，BD与反比例函数的图象交于点E，连接OE，若k＝9，点A，E分别是CD，BD的中点，求四边形OADE的面积；
(2)如图，连接OD，
(3)如图，过点A作AE⊥BO交BO于点E，过点D作DF∥BO交OA于点F，
∵四边形AOBC为菱形，∴AC∥BO，AO∥BC，∵DF∥BO，∴四边形OBDF是平行四边形，∴S△BDO＝S△DFO，同理S△ACD＝S△ADF，
(4)如图④，以AB为直角边向右构造等腰Rt△ABC，∠BAC＝90°，过点A作AD⊥y轴于点D，以AD为斜边向上构造等腰直角三角形ADE，点C，点E恰好都落在该反比例函数的图象上，若△ABC的面积为10，求△ADE的面积．
(4)如图，分别过点E作EF⊥x轴于点F，交AD于点M，BG⊥AD，CH⊥DH，垂足分别为G，H，
∵△ADE是等腰直角三角形，∴EM＝DM＝AM，∴根据反比例函数的性质可知点A，E的横坐标之比为2∶1，则它们的纵坐标之比为1∶2，∴EF＝2MF，即EM＝MF，∵△ABC是等腰直角三角形，
∴AB＝AC，∠BAC＝90°，∴∠GAB＋∠HAC＝∠GAB＋∠GBA＝90°，∴∠HAC＝∠GBA，∵∠BGA＝∠AHC＝90°，∴△ABG≌△CAH(AAS)，∴BG＝AH，设E(a，2a)，A(2a，a)，∴k＝2a2，BG＝AH＝a，
∴DH＝3a.∵点C也在反比例函数的图象上，
(1)求一次函数和反比例函数的表达式；
解：(1)∵点A(0，－4)，B(2，0)均在一次函数y＝kx＋b的图象上，
∴一次函数的表达式为y＝2x－4，∵点G(3，a)在一次函数y＝2x－4图象上，
∴a＝2，∴G(3，2)，
(2)求△DPQ面积的最大值．