数学22.2 圆的切线试讲课课件ppt

这是一份数学22.2 圆的切线试讲课课件ppt，共45页。PPT课件主要包含了第一课时，叫做直线和圆相离，直线和圆没有公共点，叫做直线和圆相切，叫直线和圆相交，直线和圆相切，直线和圆相交，直线和圆相离，切线的判定定理，切线的性质定理等内容，欢迎下载使用。

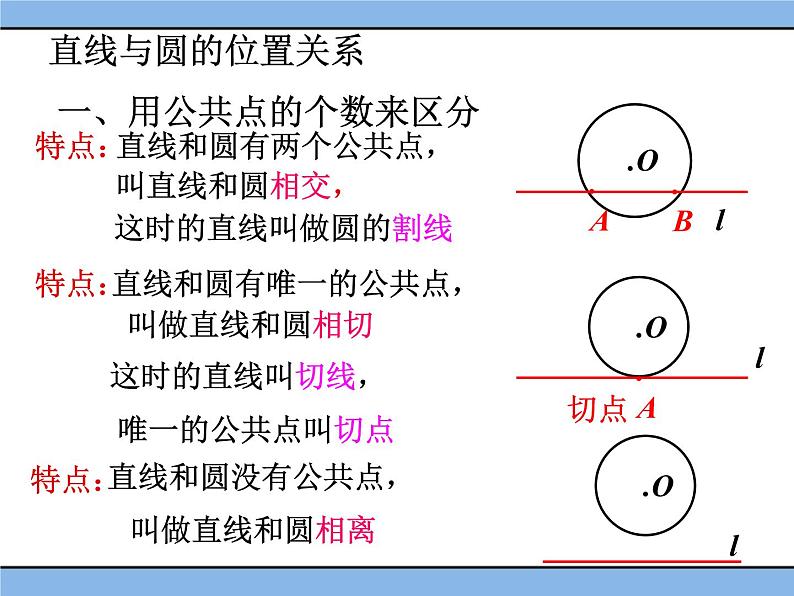
直线和圆有唯一的公共点，
这时的直线叫切线， 唯一的公共点叫切点
直线和圆有两个公共点，
这时的直线叫做圆的割线
直线与圆的位置关系 一、用公共点的个数来区分
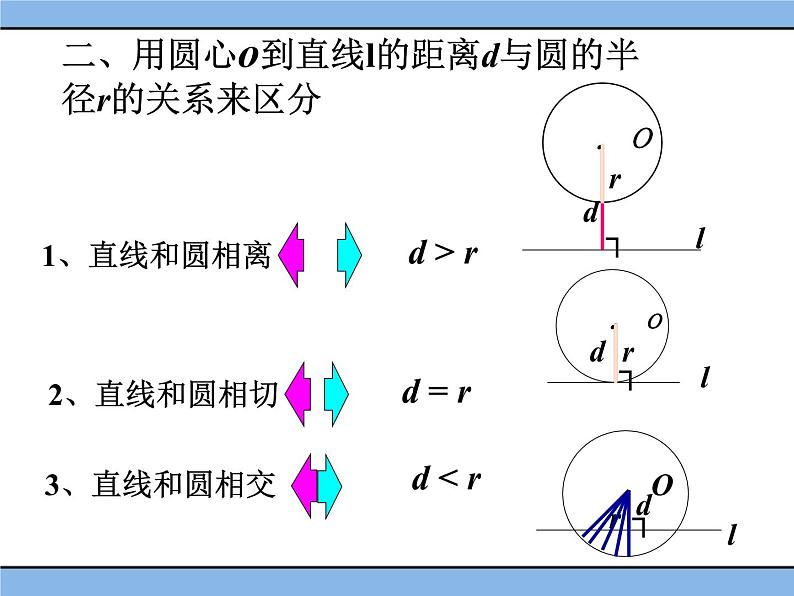
二、用圆心到直线l的距离d与圆的半径r的关系来区分
问题1：下雨天，转动的雨伞上的水滴是顺着伞的什么方向飞出去的?
问题2：砂轮转动时，火花是沿着砂轮的什么方向飞出去的?
切线的判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线.
如图：判断下列图形中的直 线a是否是圆的切线
一般情况下，要证明一条直线为圆的切线，它过半径外端是已知给出时，只需证明该直线垂直于半径.
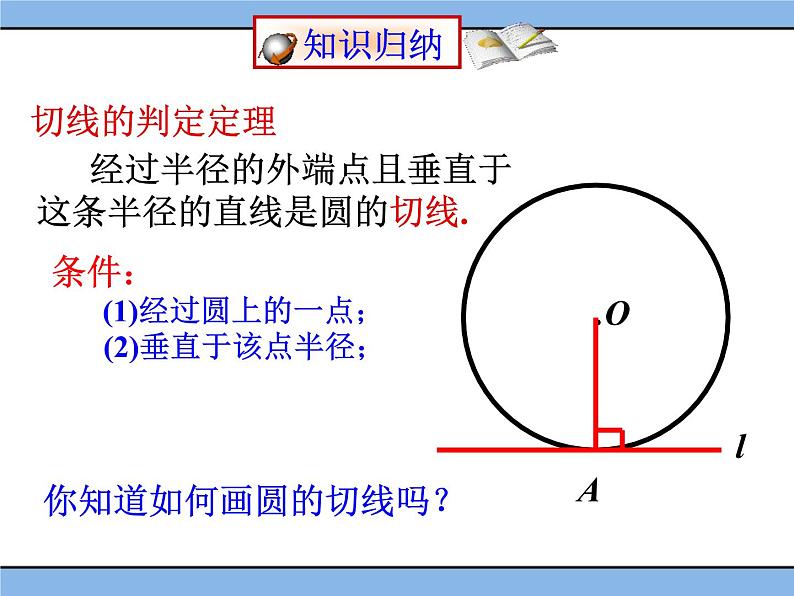
经过半径的外端点且垂直于这条半径的直线是圆的切线.
(1)经过圆上的一点；
(2)垂直于该点半径；
你知道如何画圆的切线吗？
如果直线l是⊙O的切线，点A为切点，那么半径OA与l垂直吗？
推理格式 ∵直线l是⊙ O 的切线∴ OA⊥l
圆的切线垂直于经过切点的半径.
直线AB经过圆O上的C，并且OA=OBAC=BC.求证：直线AB是圆O 的切线
证明一条直线是圆的切线时:直线与圆有交点时，连接交点与圆心，证垂直.
解：直线AC与⊙O相切.理由如下：
∴AB2+AC2=BC2.
∴△ABC为直角三角形，∠BAC=900.
∴直线AC经过⊙O半径的外端A.
∴直线AC与⊙O相切，A为切点.
证明一条直线是圆的切线的常见方法有两种：
（1）当直线和圆有一个公共点时，把圆心和这个公共点连接起来，然后证明直线垂直于这条半径，简称“作半径，证垂直”.
(2)当直线和圆的公共点没有明确时，可过圆心作直线的垂线，再证圆心到直线的距离等于半径，简称“作垂直，证半径”.
如图AB是⊙O的切线，点A是⊙O上的一点则 AB ___ OA.
切线的性质： 圆的切线垂直于经过切点的半径.
如果l是 ⊙O 的切线，A 为切点，那么AM⊥OA.你能说明理由吗？
反证法：假设l与OA不垂直则过点O作OM⊥l，垂足为M根据垂线段最短的性质， 得OM＜OA，即圆心O到直线l的距离d＜R∴直线l 与⊙O 相交这与已知“l是 ⊙O 的切线”矛盾∴假设不成立，即OA⊥l
例2 如图所示，AB是⊙O的弦，AC切⊙于点A，且∠BAC=54°，求∠OBA的度数.
∴∠OAB=90°－∠CAB=46°
∴∠OBA=∠OAB=46°
(1) 垂直于圆的半径的直线一定是这个圆的切线
(2) 过圆的半径的外端的直线一定是这个圆的切线
2.如图，AB是⊙O的直径，∠B＝45°，AC＝AB， AC是⊙O的切线吗？为什么？
解：AC是⊙O的切线 。理由如下：
又∵∠BAC＋∠B＋∠C ＝ 180°
∵ AC＝AB ， ∠B＝45°(已知)
∴∠C＝∠B＝45°(等边对等角)
∴∠ BAC ＝ 180°-∠B-∠C＝90°
3.PA、PB是⊙O的切线，切点分别为A、B，C是⊙O上一点，若∠APB=40°，求∠ACB的度数.
1、如何判定一条直线是已知圆的切线？
(1)和圆只有一个公共点的直线是圆的切线；
(2)和圆心的距离等于半径的直线是圆的切线；
(3)过半径外端且和半径垂直的直线是圆的切线；
A 、经过圆上的一点；
2、圆的切线有什么性质？
圆的切线垂直于经过切点的半径.
1.理解切线长的概念，掌握切线长定理．2.学会运用切线长定理解有关问题．3.通过对例题的分析，培养学生分析总结问题的习 惯，提高学生综合运用知识解题的能力，培养数 形结合的思想．
1.如何过⊙O外一点P画出⊙O的切线？
2.这样的切线能画出几条？
如下左图，借助三角板，我们可以画出PA是⊙O的切线.
如何用圆规和直尺作出这两条切线呢？
思考：已画出切线PA,PB，A,B为切点，则∠OAP=90°,连接OP，可知A,B 除了在⊙O上，还在怎样的圆上?
     议一议如图 ，PA，PB 是 ⊙O 的两条切线，A，B 是切点．（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？（2）在这个图中你能发现相等的线段吗？说说你的理由．
过圆外一点作圆的切线，这点和切点之间的线段长叫做这点到圆的切线长.
切线与切线长是一回事吗？它们有什么区别与联系呢？
切线和切线长是两个不同的概念：1.切线是一条与圆相切的直线，不能度量；2.切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量.
思考：已知⊙O切线PA，PB，A，B为切点，把圆沿着直线OP对折，你能发现什么?
请证明你所发现的结论.
证明：∵PA，PB与⊙O相切，点A，B是切点，∴OA⊥PA，OB⊥PB.即∠OAP=∠OBP=90°，∵ OA=OB，OP=OP，∴Rt△AOP≌Rt△BOP(HL)∴ PA = PB， ∠OPA=∠OPB.
∵PA，PB分别切⊙O于A，B，∴PA=PB,OP平分∠APB.
过圆外一点所画的圆的两条切线长相等.
反思：切线长定理为证明线段相等、角相等提供新的方法
若连接两切点A，B，AB交OP于点M.你又能得出什么新的结论?并给出证明.
证明：∵PA，PB是⊙O的切线，点A，B是切点，∴PA=PB，∠OPA=∠OPB.∴△PAB是等腰三角形，PM为顶角的平分线.∴OP垂直平分AB.
（3）连接圆心和圆外一点
（1）分别连接圆心和切点
反思：在解决有关圆的切线长问题时，往往需要我们构建基本图形.
探究：PA，PB是⊙O的两条切线，A，B为切点，直线OP交⊙O于点D，E，交AB于点C.
（1）写出图中所有的垂直关系
OA⊥PA OB⊥PB AB⊥OP
（2）写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
△AOP≌△BOP，△AOC≌△BOC，△ACP≌△BCP
（4）写出图中所有的等腰三角形
（3）写出图中所有的全等三角形
内切圆圆心：三角形三个内角平分线的交点内切圆的半径：交点到三角形任意一边的垂直距离
这个三角形称为这个圆的外切三角形.
内切圆圆心叫做三角形的内心.
例3 如图，Rt△ABC 的两条直角边 AC = 10，BC = 24，⊙O 是△ABC 的内切圆，切点分别为D，E，F，求 ⊙O 的半径．
解：连接 OD，OE，OF，设 OD = r．　　在 Rt△ABC 中，AC = 10，BC = 24,　　∵ ⊙O 分别与 AB，BC，CA 相切于点 D，E，F，
∴ OD⊥AB，OE⊥BC，OF⊥AC，BE =BD， AF =AD， CE =CF.又∵ ∠C = 90° ，∴ 四边形OECF 为正方形.∴EC = FC = r. BE = 24 –r，AF = 10 - r.∴AB =BD + AD = BE + AF = 34 - 2r = 26.∴ r = 4,即 ⊙O半径为4.
例4 △ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=9cm，BC=14cm，CA=13cm，求AF，BD，CE的长.
设AF=x,则AE=x
∴CD=CE=AC-AE=13-x，BD=BF=AB-AF=9-x.
由BD+CD=BC可得13-x+9-x=14，
∴ AF=4 cm, BD=5 cm, CE=9 cm.
如图 ，四边形 ABCD 的四条边都与 ⊙O 相切，图中的线段之间有哪些等量关系？与同伴进行交流．
证明：由切线长定理得AL=AP，LB=MB，NC=MC，DN=DP,∴AP+MB+MC+DP=AL+LB+NC+DN,即AD+BC=AB+CD，补充：圆的外切四边形的两组对边的和相等．
1.如图，PA,PB是⊙O的切线，切点分别是A,B，如果∠P＝60°,那么∠PAB等于（ ）
A.60° B.90°C.120° D.150°
2. PA，PB是⊙O的两条切线，A，B为切点，直线OP交⊙O于点D，E，交AB于点C.如果PA=4cm,PD=2cm,求半径OA的长.
【解析】设OA=xcm；
在Rt△OAP中，OA=xcm，OP=OD+PD=（x+2）cm，PA=4cm,
由勾股定理，得PA2+OA2=OP2，
即42+x2=(x+2)2,
所以，半径OA的长为3cm.