华东师大数学八年级上册 14《章末复习》PPT课件

这是一份华东师大数学八年级上册 14《章末复习》PPT课件，共35页。

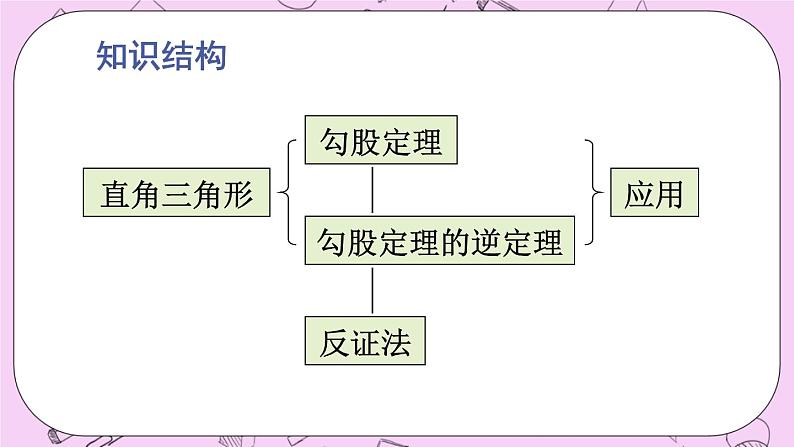
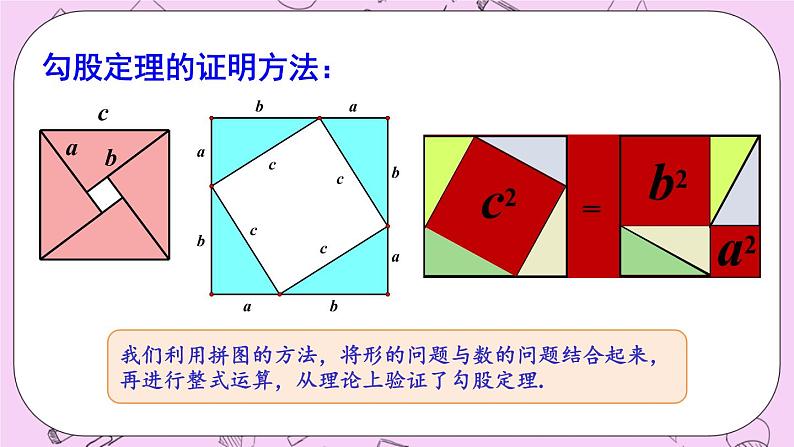
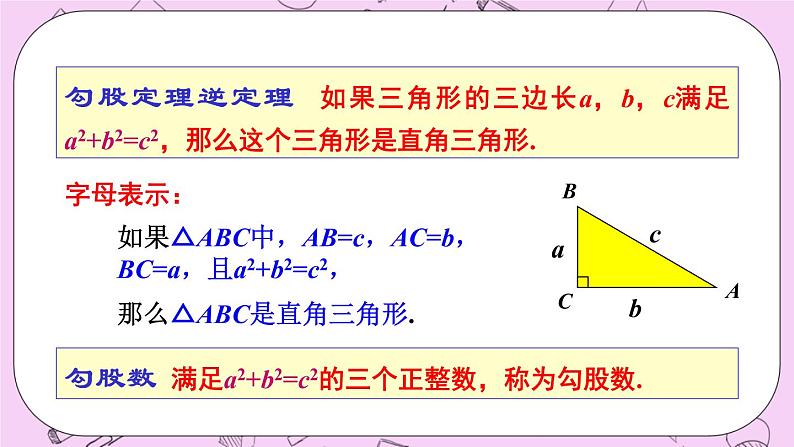
华东师大版数学八年级上册14《章末复习》知识结构直角三角形勾股定理勾股定理的逆定理应用反证法思考并回答下列问题：问题1：勾股定理与逆定理的内容是什么？问题2：勾股定理与逆定理的证明方法是怎样的，它们各体现什么样的数学思想？你是怎样理解的？问题3：如何判定一个三角形是直角三角形？问题4：反证法的步骤是什么？要 点勾股定理 如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2.AB如果在Rt△ABC中，∠C=90°，字母表示：那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理的证明方法：我们利用拼图的方法，将形的问题与数的问题结合起来，再进行整式运算，从理论上验证了勾股定理.勾股定理逆定理 如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形.ABC字母表示：如果△ABC中，AB=c，AC=b，BC=a，且a2+b2=c2，那么△ABC是直角三角形.勾股数 满足a2+b2=c2的三个正整数，称为勾股数.反证法是从反面的角度着手的间接证明方法，即：肯定条件而否定结论，从而得出矛盾，使命题获得证明.反证法是数学中常用的一种证明方法.当命题从正面不容易或不能得到证明时，就可以考虑运用反证法.典例精析例1（1）下列命题中正确的是（ ） A.1.5，2，2.5是勾股数 B.至少有一个角大于60°的反面是至多有一个角大于60° C.边长为3a，4a，5a的三角形是直角三角形 D.直角三角形的两边是3和4，它的面积是6C（2）如图，每个小正方形的边长为1，点A、B、C是小正方形的顶点，则∠ABC=_________.（3）如图，长方形ABCD中，AB=15cm，点E在AD上，且AE=9cm，连结EC将长方形沿BE翻折，点A恰好落在EC上的点A′处，则A′C=____cm.45°8例2 如图圆柱形的玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底4cm的C处有一滴蜂蜜，此时一只蚂蚁正好在外壁离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离是多少厘米？解：画出全半侧面的展开图，如图，则EF=9cm，AE=4cm，CM=4cm，取点A关于直线EF的对称点A′，则A′E=4cm，连结A′C交EF于P，则PA+PC最短，作GC⊥EN于G，在Rt△A′GC中，AP+PC= =15(cm).例3 在Rt△ABC中，已知两直角边a与b的和为pcm，斜边长为qcm，求这个三角形的面积.例4 如图所示，有一个正方形水池，每边长4米，池中央长了一棵芦苇，露出水面1米，把芦苇的顶端引到岸边，芦苇顶和岸边水面刚好相齐，你能算出水池的深度吗？解：设水池深为x米，BC=x米，AC=(x+1)米，因为池边长为4米，所以BA′=2米，在Rt△A′BC中，根据勾股定理得x2+22=(x+1)2，解得x=1.5.例5 如图所示，△ABC中，AB=26，BC=20，BC边上的中线AD=24，求AC. 例6 已知，如图，在四边形ABCD中，∠ABC=90°，CD⊥AD于点D，且CD2+AD2=2AB2.(1)求证AB=BC；(2)当BE⊥AD于点E时，试证明：BE=AE+CD.(1)证明：由条件CD2+AD2=2AB2，并结合图形，有CD2+AD2=AC2，又AC2=AB2+BC2(连结AC)，从而2AB2=AB2+BC2，有BC=AB；(2)证明：过C作CF⊥BE于F，由AB=BC，∠ABE=∠BCF，∠AEB=∠CFB，知△ABE≌△BCF，有BF=AE，且CD=FE，∴BE=BF+EF=AE+CD.F复习题1.求下列各图形着色部分的面积：(1)着色部分是正方形； (2)着色部分是长方形；A组12cm13cm15cm8cm3cmS=132-122=25(cm2).(3)着色部分是半圆.6cm10cm2.如图，以Rt△ABC的三边为斜边分别向外作三个等腰直角三角形，试探索这三个等腰直角三角形的面积之间的关系.解：以a、b为斜边的两个等腰直角三角形的面积等于以c为斜边的等腰直角三角形的面积．3.试判断由下列三边围成的三角形是否是直角三角形：(1)三边长分别为m2+ n2、mn、m2-n2(m>n>0)；(2)三边长之比为1∶1∶ .不是是4.一架2.5米长的梯子靠在一座建筑物上，梯子的底部离建筑物0.7米，如果梯子的顶部滑下0.4米，梯子的底部向外滑出多远？解：设下滑之前，梯子顶部到地面的距离为下滑0.4米之后，梯子顶部到地面的距离h2=2.4-0.4=2(米)，梯子底部离建筑物的距离梯子底部向外滑出1.5-0.7=0.8(米).所以梯子底部向外滑出0.8米.5.在如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为7cm.求正方形A、B、C、D的面积和.ABEFCDG解：SA+SB+SC+SD =SE+SF =SG=72=49(cm2).6.在△ABC中，AB=AC=10，BD是AC边上的高，DC=2.求BD的长.B组7.有一块四边形地ABCD(如图)，∠B=∠90°. AB=4m，BC=3m，CD=12m，DA=13m.求该四边形地的面积.AC2+CD2=52+122=132=AD2，由勾股定理的逆定理得∠ACD=90°，所以S四边形ABCD=S△ACD+S△ABC8.我们已经知道，3、4、5，6、8、10 等都是一些勾股数.请你再写出其他5组勾股数.解：5，12，13；7，24，25；8，15，17；9，12，15；12，16，20(答案不唯一).9.试证明一个五边形不可能有4个内角为锐角.证明：假设五边形有四个内角是锐角，那么与它们相邻的四个外角均为钝角，其和大于360°，与多边形外角和为360°矛盾，所以假设不成立，故五边形不可能有4个内角为锐角.C组10.已知△ABC的三边长a、b、c满足条件：a4-b4+b2c2-a2c2=0.试判断△ABC的形状.解：因为a4-b4+b2c2-a2c2=0，∴(a2+b2)(a2-b2)+c2(b2-a2)=0，∴(a2-b2)·(a2+b2-c2)=0，∴a2-b2=0或a2+b2-c2=0，∴a+b=0(舍)或a=b或a2+b2=c2，∴△ABC为等腰三角形或直角三角形.11.如图，在四边形ABCD中，AB=BC=2，CD=3，DA=1，且∠B=90°.求∠DAB的大小.解：连接AC，∵AB=BC=2，∠B=90°，在△ACD中，AD2+AC2=9=CD2，∴△ACD中是直角三角形，∠DAC=90°，∴∠DAB=∠DAC+∠BAC=135°.12.如图，在五边形ABCDE中，∠B=∠E=90°，AB=5cm，△ABC的面积是30cm2，△ACD与△AED关于AD所在的直线成轴对称.求AE的长.又∵△ACD与△AED关于AD所在的直线成轴对称，∴AE=AC=13cm.13.折竹抵地（源自《九章算术》）： 今有竹高一丈，末折抵地，去本三尺.问折者高几何？意即：一根竹子，原高一丈，虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子处3尺远.问原处还有多高的竹子？解：设原处还有x尺高的竹子，由勾股定理得x2+32=(10-x)2，答：原处还有4.55尺高的竹子.课后作业1.从课后习题中选取；2.完成练习册本课时的习题.