















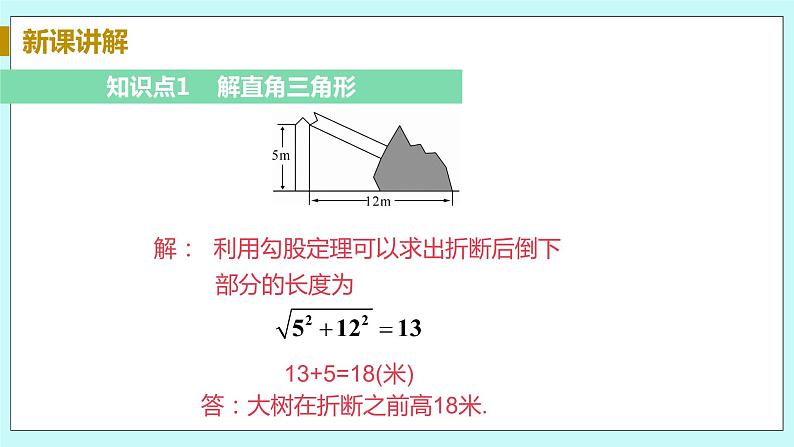










数学九年级上册第24章 解直角三角形24.4 解直角三角形评优课课件ppt
展开24.4 解直角三角形
一、选择题
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AB=c,∠a=α,则CD的长为( )
(第1题图)
A. c • sin2α B. c • cos2α
C. c• sin α• tan α D. c • sin α • cos α
2. 数学活动课上,小敏和小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC,S△DEF,那么它们的大小关系是( )
(第2题图)
A. S△ABC >S△DEF B. S△ABC <S△DEF C. S△ABC = S△DEF D. 不能确定
3. 如图,在Rt△ABC中,∠C=90°,若AB=5,sin A=,则AC的长是( )
(第3题图)
A. 3 B. 4 C. 5 D. 6
4. 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB. 其中能根据所测数据求得A,B两树距离的有( )
(第4题图)
A. 0组 B. 1组 C. 2组 D. 3组
5. 在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin 18°≈0.31,tan 18°≈0.32,sin 66°≈0.91,tan 66°≈2.2)( )
(第5题图)
A. 1.2米 B. 1.5米 C. 1.9米 D. 2.5米
6. 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
(第6题图)
A. 5米 B. 6米 C. 8米 D.(3+)米
7. 如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.则放水后水面上升的高度是( )
(第7题图)
A. 0.55 B. 0.8 C. 0.6 D. 0.75
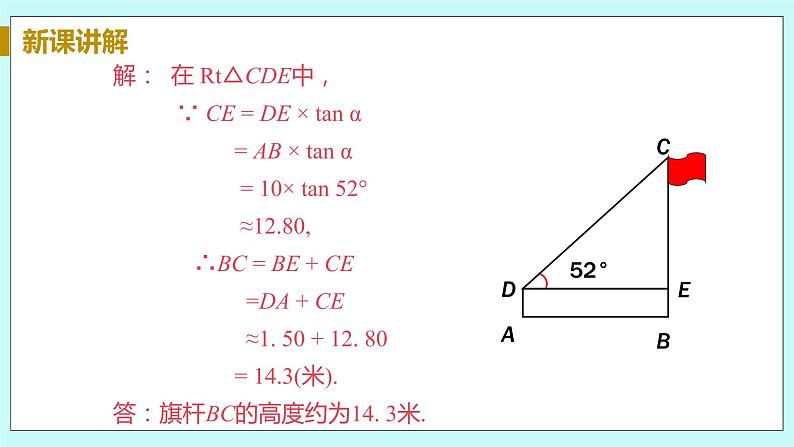
8. 湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
(第8题图)
A. 34米 B. 38米 C. 45米 D. 50米
9. 在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走菁优网了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A. 北偏东20°方向上 B. 北偏西20°方向上
C. 北偏西30°方向上 D. 北偏西40°方向上
二、填空题
10. 如图,港口A在观测站O的正东方向,OA=4 km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 km.
(第10题图)
三、解答题
11. 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
(第11题图)
12. 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)
(第12题图)
参考答案
一、1. D 分析:在Rt△ABC中,∵∠ACB=90°,AB=c,∠A=α,sin α=,∴BC=c • sin α. ∵∠A+∠B=90°,∠DCB+∠B=90°,∴∠DCB=∠A=α.在Rt△DCB中,∵∠CDB=90°,cos∠DCB=,∴CD=BC • cos α=c • sin α • cos α.故选D.
2. C 分析:如答图,分别过点A,D作AG⊥BC,DH⊥EF,垂足分别为G,H.在Rt△ABG中,AG=AB • sin B=5×sin 50°=5sin 50°.在Rt△DHE中,∠DEH=180°- 130°=50°,∴DH=DE • sin∠DEH=5sin 50°,∴AG=DH.∵BC=4,EF=4,∴S△ABC=S△DEF.故选C.
(第2题答图)
3. B 分析:∵∠C=90°,sin A=,AB=5,∴BC=AB •sin A=5×=3. 由勾股定理,得AC==4.故选B.
4. D 分析:第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长.第②组中可利用∠ACB和∠ADB的正切求出AB.第③组中设AC=x,AD=CD+x,AB=,AB=. 因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB. 故选D.
5. B 分析:设CD为x. 在Rt△BCD中,∠BDC=α=18°. ∵tan∠BDC=,∴BC=CD•tan∠BDC=0.32x. 在Rt△ACD中,∠ADC=β=66°. ∵tan∠ADC=,∴AC=CD•tan∠ADC=2.2x. ∵AB=AC -BC,∴2.82=2.2x-0.32x,解得x=1.5. 故CD长约为1.5米.故选B.
6. A 分析:设CD=x,则AD=2x.由勾股定理,得AC=.∵AC=3米,∴x=3,解得x=3. ∴CD=3米,∴AD=2×3=6(米). 在Rt△ABD中,BD==8(米),∴BC=8-3=5(米).故选A.
7. D 分析:如答图,过点E作EM⊥GH于点M. ∵水渠的横断面是等腰梯形,∴GM=×(GH-EF)=×(2.1-1.2)=0.45.∵斜坡AD的坡度为1:0.6,∴EM:GM=1:0.6,∴EM:0.45=1:0.6,∴EM=0.75. 故选D.
(第7题答图)
8. C 分析:过点D作DE⊥AB于点E,则DE=BC=50米. 在Rt△ADE中,AE= DE•tan41,5°≈50×0.88=44(米). ∵CD=1米,∴BE=1米,∴AB=AE+BE=44+1=45(米),∴桥塔AB的高度为45米.
9. B 分析:如答图.∵AC=10千米,AB=8千米,BC=6千米,∴AC2=AB2+BC2,∴△ABC为直角三角形,即∠ABC=90°,又∵B点在A的北偏东70°方向,∴∠1= 90°-70°=20°,∴∠2=∠1=20°,即C点在B的北偏西20°的方向上.故选B.
(第9题答图)
二、 10. 2 分析:如答图,过点A作AD⊥OB于点D. 在Rt△AOD中,∵∠ADO= 90°,∠AOD=30°,OA=4 km,∴AD=OA=2(km).在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB-∠AOB=75°-30°=45°,∴BD=AD=2 km,∴AB=AD=2(km).即该船航行的距离(即AB的长)为2km.
(第10题答图)
三、11. 解:连接EC,如答图.
∵四边形ABCD为矩形,
∴OA=OC,∠ABC=90°.
由勾股定理,得AC==10,即OA=5.
∵OE⊥AC,∴AE=CE.
在Rt△EDC中,设EC=AE=x,则有ED=AD -AE=8-x,DC=AB=6.
根据勾股定理,得x2=(8-x)2+62.解得x=.
∴AE=.
在Rt△AOE中,sin∠OEA=.
(第11题答图)
12. 解:需要拆除.理由如下:
∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米.
在Rt△BCD中,新坡面DC的坡度为i=:3,即∠CDB=30°,
∴DC=2BC=20米,BD=(米),
∴AD=BD -AB=10-10≈7.32(米).
∵3+7.32=10.32>10,
∴需要拆除.
初中数学华师大版九年级上册24.1 测量优质课课件ppt: 这是一份初中数学华师大版九年级上册24.1 测量优质课课件ppt,文件包含241测量课件pptx、习题241测量doc、教案241测量doc等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
华师大版九年级上册2. 图形的变换与坐标优秀课件ppt: 这是一份华师大版九年级上册2. 图形的变换与坐标优秀课件ppt,文件包含2362图形变换与坐标变化课件pptx、2361用坐标确定位置课件pptx、习题236图形与坐标doc、教案2362图形的交换与坐标doc、教案2361用坐标确定位置doc等5份课件配套教学资源,其中PPT共40页, 欢迎下载使用。
数学九年级上册23.5 位似图形优秀ppt课件: 这是一份数学九年级上册23.5 位似图形优秀ppt课件,文件包含235位似图形课件pptx、习题235位似图形doc、教案235位似图形doc等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。













