





初中青岛版1.2 怎样判定三角形相似一等奖教学ppt课件
展开1.2 怎样判定三角形相似(1)
【学习内容】教材P8-11
【学习目标】
1、 理解掌握平行线分线段成比例定理
2、三角形相似的预备定理:
【学习重点】1、理解掌握平行线分线段成比例定理及应用.
2、三角形相似的预备定理
【学习难点】1、掌握平行线分线段成比例定理应用.
2、三角形相似的预备定理应用.
【学习过程】
一、学生回顾,教师导学:
1、相似多边形的主要特征是什么?
2、相似三角形有什么性质?
3、在相似多边形中,最简单的就是相似三角形.
在△ABC与△A′B′C′中,
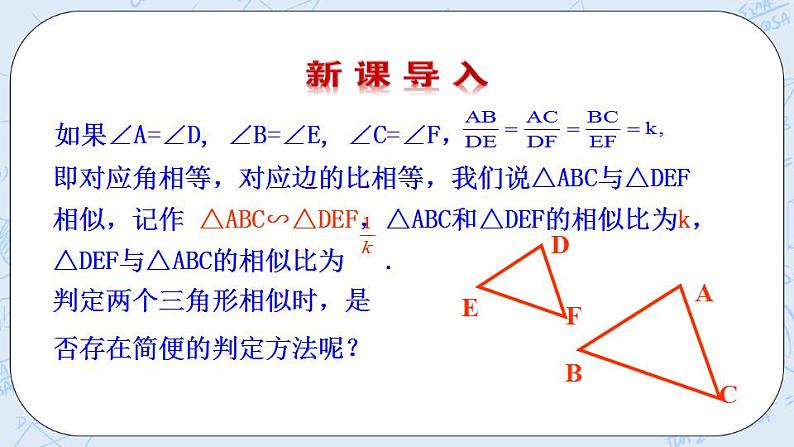
如果∠A=∠A′, ∠B=∠B′, ∠C=∠C′, 且.
我们就说△ABC与△A′B′C′相似,记作△ABC∽△A′B′C′,k就是它们的相似比.
反之如果△ABC∽△A′B′C′,
则有∠A=_____, ∠B=_____, ∠C=____, 且.
4、问题:(1)如果k=1,这两个三角形有怎样的关系?
(2)当△ABC与△的相似比为k时,△与△ABC的相似比为_______
二、学生探究,教师引领
[活动1] (教材P8-9探究)
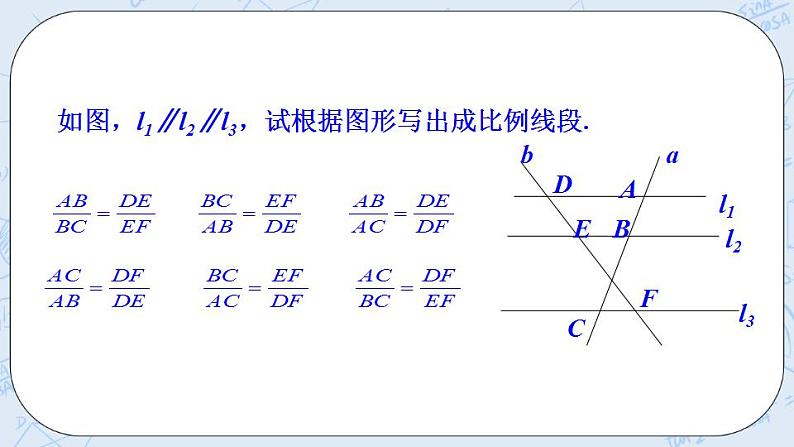
(1) 如图,任意画两条直线l1 , l2,再画三条与l1 , l2 相交的平行线l3 , l4, l5.分别量度l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB:BC 与DE:EF相等吗?任意平移l5 , 再量度AB, BC, DE, EF的长度, AB:BC 与DE:EF相等吗?
(2)问题,AB:AC=DE:( ),BC:AC=( ):DF.
(3) 归纳总结:
平行线分线段成比例定理:三条_______截两条直线,所得的________线段的比________.
(4) 例 如图、若AB=3cm,BC=5cm,EK=4cm,写出=_____=_____、_____=______. 求FK的长?
[活动2]平行线分线段成比例定理推论
思考:1、如果把图中l1 , l2两条直线相交,交点A刚落到l3上,如图(1),,所得的对应线段的比会相等吗?依据是什么?
2、 如果把图中l1 , l2两条直线相交,交点A刚落到l4上,如图(2),所得的对应线段的比会相等吗?依据是什么?
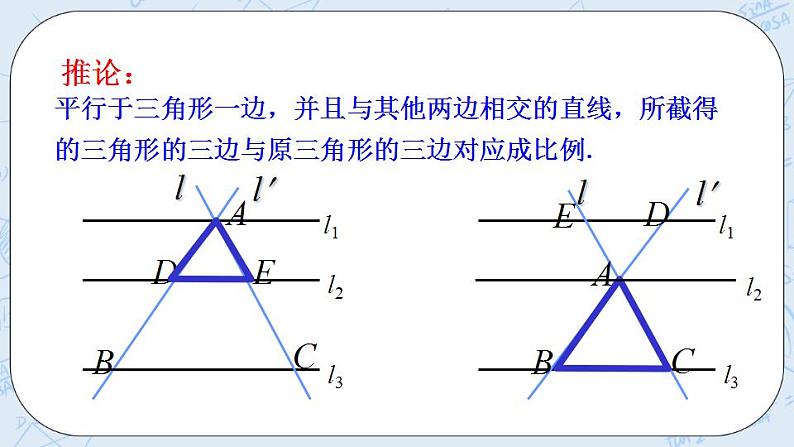
3、 归纳总结:
平行线分线段成比例定理推论 平行于三角形一边的直线截其他两边(或两边延长线),所得的_______线段的比_________.
4、如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
[活动3]
1 问题:如果△ABC∽△ADE,那么你能找出哪些角的关系?边呢?
2 思考
如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E.问题:
(1) △ADE与△ABC满足“对应角相等”吗?为什么?
(2) △ADE与△ABC满足对应边成比例吗?由“DE∥BC”的条件可得到哪些线段的比相等?
(3) 根据以前学习的知识如何把DE移到BC上去?(作辅助线EF∥AB)
你能证明AE:AC=DE:BC吗?
(4)写出△ABC∽△ADE的证明过程.
(5)归纳总结:判定三角形相似的(预备)定理:
平行于三角形一边的直线和其他两边相交,所成的三角形 .
(6)如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.
解:
三、学生展示,教师激励
展示各学习小组合作探究结果.
四、学生归纳,教师提炼
1、你对同学有那些温馨的提示?____________
2、你还需要老师为你解决那些问题?____________
五、学生达标,教师测评
1.(选择)下列各组三角形一定相似的是( )
A.两个直角三角形 B.两个钝角三角形
C.两个等腰三角形 D.两个等边三角形
2.(选择)如图,DE∥BC,EF∥AB,则图中相似三角形一共有( )
A.1对 B.2对 C.3对 D.4对
3. 如图,AB∥EF∥CD,图中共有 对相似三角形,写出来并说明理由.
4.如图,在中,EF∥AB,DE:EA=2:3,EF=4,求CD的长.
教(学)后感:
初中数学青岛版九年级上册3.2 确定圆的条件公开课教学ppt课件: 这是一份初中数学青岛版九年级上册3.2 确定圆的条件公开课教学ppt课件,文件包含《确定圆的条件1》课件ppt、《确定圆的条件1》教学设计doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
九年级上册3.1 圆的对称性完美版教学ppt课件: 这是一份九年级上册3.1 圆的对称性完美版教学ppt课件,文件包含《圆的对称性1》课件ppt、《圆的对称性1》教学设计doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
青岛版九年级上册第3章 对圆的进一步认识3.3 圆周角优质教学课件ppt: 这是一份青岛版九年级上册第3章 对圆的进一步认识3.3 圆周角优质教学课件ppt,文件包含《圆周角1》课件ppt、《圆周角1》教学设计doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













