









高中湘教版(2019)3.1 函数获奖ppt课件
展开4.1.3 幂函数
课标要求 1.了解幂函数的概念,会求幂函数的解析式.2.通过具体实例,结合y=x,y=x2,y=x3,y=x-1,y=x的图象,理解它们的变化规律,了解幂函数.
素养要求 以五个常见幂函数为载体,归纳幂函数的图象与性质,发展学生的数学抽象、逻辑推理素养.
自 主 梳 理
1.幂函数
当x为自变量而α为非零实数时,函数y=xα叫作(α次)幂函数.
2.实数次幂函数y=xα的性质(α≠0)
(1)当α>0时,它在[0,+∞)有定义且递增,值域为[0,+∞),函数图象过(0,0)和(1,1)两点;
(2)当α<0时,它在(0,+∞)有定义且递减,值域为(0,+∞),函数图象过(1,1),向上与y轴正向无限接近,向右与x轴正向无限接近.
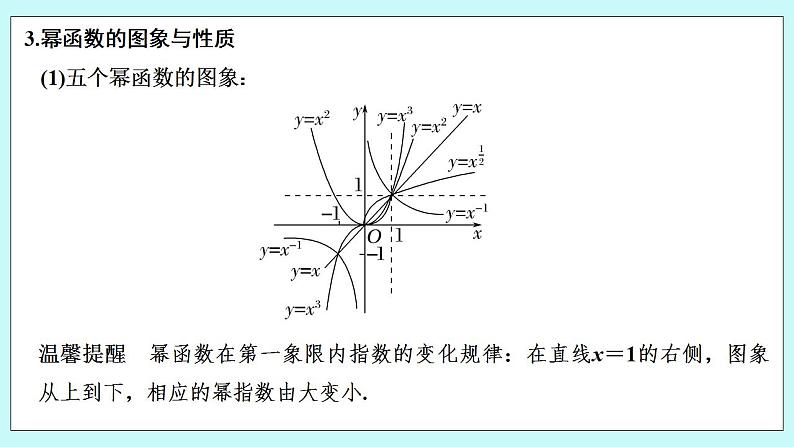
3.幂函数的图象与性质
(1)五个幂函数的图象:
温馨提醒 幂函数在第一象限内指数的变化规律:在直线x=1的右侧,图象从上到下,相应的幂指数由大变小.
(2)幂函数的性质:
幂函数 | y=x | y=x2 | y=x3 | y=x | y=x-1 |
定义域 | R | R | R | [0,+∞) | (-∞,0)∪(0,+∞) |
值域 | R | [0,+∞) | R | [0,+∞) | {y|y∈R,且y≠0} |
奇偶性 | 奇 | 偶 | 奇 | 非奇非偶 | 奇 |
单调性 | 增 | x∈[0,+∞),增 x∈(-∞,0],减 | 增 | 增 | x∈(0,+∞),减 x∈(-∞,0),减 |
公共点 | 都经过点(1,1) | ||||
自 主 检 验
1.思考辨析,判断正误
(1)函数y=x2是幂函数.(√)
(2)幂函数的图象都过点(1,1).(√)
2.下列所给的函数中是幂函数的为( )
A.y=2x5 B.y=x3+1
C.y=x-3 D.y=3x
答案 C
解析 选项C符合y=xα的形式,
对于A系数不为1,
B中含有常数项,
而D不符合y=xα的形式.
3.已知幂函数y=xα的图象经过点(2,4),则f(-3)=________.
答案 9
解析 由于幂函数y=xα的图象经过点(2,4),即2α=4,解得α=2,
故f(-3)=(-3)2=9.
4.3.17-1与3.71-1的大小关系为___________________________.
答案 3.17-1>3.71-1
题型一 幂函数的概念
例1 (1)在函数y=x-2,y=2x2,y=(x+1)2,y=3x中,幂函数的个数为( )
A.0 B.1
C.2 D.3
(2)若f(x)=(m2-4m-4)xm是幂函数,则m=________.
答案 (1)B (2)5或-1
解析 (1)根据幂函数定义可知,只有y=x-2是幂函数,所以选B.
(2)因为f(x)是幂函数,所以m2-4m-4=1,即m2-4m-5=0,解得m=5或m=-1.
思维升华 判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,需满足:①指数为常数,②底数为自变量,③xα系数为1.形如y=(3x)α,y=2xα,y=xα+5,…,形式的函数都不是幂函数.反过来,若一个函数为幂函数,则该函数也必具有这一形式.
训练1 函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.
解 根据幂函数定义得,
m2-m-1=1,解得m=2或m=-1,
当m=2时,f(x)=x3,在(0,+∞)上是增函数,
当m=-1时,f(x)=x-3,在(0,+∞)上是减函数,不合要求.∴f(x)的解析式为f(x)=x3.
题型二 幂函数的图象及应用
例2 如图所示,图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
答案 B
解析 根据幂函数y=xn的性质,在第一象限内的图象当n>0时,n越大,y=xn递增速度越快,故C1的n=2,C2的n=;当n<0时,|n|越大,曲线越陡峭,所以曲线C3的n=-,曲线C4的n=-2,故选B.
思维升华 解决幂函数图象问题应把握的两个原则
(1)依据图象高低判断幂的指数大小,相关结论为:
①在(0,1)上,幂的指数越大,幂函数图象越靠近x轴(简记为指大图低);②在(1,+∞)上,幂的指数越大,幂函数图象越远离x轴(简记为指大图高).
(2)依据图象确定幂的指数α与0,1的大小关系,即根据幂函数在第一象限内的图象(类似于y=x-1或y=x或y=x3)来判断.
训练2 如图是幂函数y=xm与y=xn在第一象限内的图象,则( )
A.-1<n<0<m<1 B.n<-1,0<m<1
C.-1<n<0,m>1 D.n<-1,m>1
答案 B
解析 在(0,1)内取同一值x0,作直线x=x0,与各图象有交点,如图所示.
根据点低指数大,有0<m<1,n<-1.
题型三 幂函数的性质及应用
例3 比较下列各组数中两个数的大小:
(1)与;(2)与.
解 (1)因为幂函数y=x0.3在(0,+∞)上是增函数,且>,所以>.
(2)因为幂函数y=x-1在(-∞,0)上是减函数,且-<-,
所以>.
思维升华 比较幂值大小的两种基本方法
训练3 比较下列各组数的大小:
(1)与;(2)-3.143与-π3.
解 (1)∵y=x0.5在[0,+∞)上是增函数且>,
∴>.
(2)∵y=x3是R上的增函数,且3.14<π,
∴3.143<π3,∴-3.143>-π3.
[课堂小结]
1.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数,这是判断一个函数是不是幂函数的重要依据和唯一标准.
2.幂函数y=xα的图象与性质由于α的值不同而比较复杂,一般从两个方向考查:(1)α>0时,图象过(0,0),(1,1),在第一象限的图象上升;α<0时,图象不过原点,在第一象限的图象下降,反之也成立.
(2)曲线在第一象限的凹凸性:α>1时,曲线下凸;0<α<1时,曲线上凸;α<0时,曲线下凸.
一、基础达标
1.下列函数是幂函数的是( )
A.y=5x B.y=x5
C.y=5x D.y=(x+1)3
答案 B
解析 函数y=5x的底数是常数,指数是自变量x,不是幂函数;
函数y=5x是正比例函数,不是幂函数;
函数y=(x+1)3的底数不是自变量x,不是幂函数;
函数y=x5是幂函数.
2.函数y=x的图象大致是( )
答案 B
解析 函数y=x=的定义域为R,且此函数在定义域上是增函数,排除A,C.
另外,因为>1,在第一象限图象下凸.故选B.
3.如图所示,曲线C1与C2分别是函数y=xm和y=xn在第一象限内的图象,则下列结论正确的是( )
A.n<m<0 B.m<n<0
C.n>m>0 D.m>n>0
答案 A
解析 由图象可知,两函数在第一象限内递减,故m<0,n<0.
由幂函数图象的特点知n<m,故n<m<0.
4.幂函数f(x)=xm-2(m∈N)在(0,+∞)上是减函数,且f(-x)=f(x),则m可能等于( )
A.0 B.1
C.2 D.0或1
答案 A
解析 因为f(x)=xm-2(m∈N)在(0,+∞)上是减函数,所以m-2<0,故m<2.
又因为m∈N,所以m=0或m=1,
当m=0时,f(x)=x-2,f(-x)=f(x),符合题意;
当m=1时,f(x)=x-1,f(-x)≠f(x),不符合题意.
综上知,m=0.
5.(多选)已知不相等的实数a,b满足等式a=b,则下列结论可能成立的是( )
A.0<b<a<1 B.-1<a<b<0
C.1<a<b D.-1<b<a<0
答案 AC
解析 首先画出y1=x与y2=x的图象(如图),已知a=b=m,作直线y=m.
若m=0或1,则a=b;若0<m<1,
则0<b<a<1;
若m>1,则1<a<b.由图象知,成立的是A,C.
6.幂函数y=f(x)的图象经过点(2,),则满足f(x)=-27的x值等于________.
答案 -
解析 设f(x)=xα,
由题意可知2α=,α=-3,
即f(x)=x-3.
由x-3=-27可知x=-.
7.幂函数f(x)=(m2-m-1)·xm2-2m-3在(0,+∞)上是减函数,则实数m=________.
答案 2
解析 ∵f(x)=(m2-m-1)x m2-2m-3为幂函数,
∴m2-m-1=1,∴m=2或m=-1.
当m=2时,f(x)=x-3在(0,+∞)上是减函数,
当m=-1时,f(x)=x0=1不符合题意.
综上可知m=2.
8.给出以下结论:
①当α=0时,函数y=xα的图象是一条直线;
②幂函数的图象都经过(0,0),(1,1)两点;
③若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大;
④幂函数的图象不可能在第四象限,但可能在第二象限.
则正确结论的序号为________.
答案 ④
解析 当α=0时,函数y=xα的定义域为{x|x≠0,x∈R},故①不正确;
当α<0时,函数y=xα的图象不过(0,0)点,故②不正确;
幂函数y=x-1的图象关于原点对称,但其在定义域内不是增函数,故③不正确.④正确.
9.已知函数f(x)=(m2+2m)·x m2+m-1,m为何值时,函数f(x)是:(1)正比例函数;(2)反比例函数;(3)幂函数?
解 (1)若函数f(x)为正比例函数,则
∴m=1.
(2)若函数f(x)为反比例函数,则
∴m=-1.
(3)若函数f(x)为幂函数,则m2+2m=1,
∴m=-1±.
10.比较下列各组中两个值的大小:
(1)1.5与1.6;(2)0.61.3与0.71.3;
(3)3.5-与5.3-;(4)0.18-0.3与0.15-0.3.
解 (1)∵幂函数y=x在(0,+∞)上单调递增,且1.5<1.6,∴1.5<1.6.
(2)∵幂函数y=x1.3在(0,+∞)上单调递增,且0.6<0.7,∴0.61.3<0.71.3.
(3)∵幂函数y=x-在(0,+∞)上单调递减,且3.5<5.3,∴3.5->5.3-.
(4)∵幂函数y=x-0.3在(0,+∞)上单调递减,且0.18>0.15,∴0.18-0.3<0.15-0.3.
二、能力提升
11.对于幂函数f(x)=x,若0<x1<x2,则f,的大小关系是( )
A.f> B.f<
C.f= D.无法确定
答案 A
解析 幂函数f(x)=x在(0,+∞)上单调递增,大致图象如图所示.设A(x1,0),C(x2,0),其中0<x1<x2,则AC的中点E的坐标为,|AB|=f(x1),|CD|=f(x2),|EF|=f.
∵|EF|>(|AB|+|CD|),
∴f>,故选A.
12.已知幂函数f(x)=x,若f(10-2a)<f(a+1),则a的取值范围是________.
答案 (3,5]
解析 因为f(x)=x(x≥0),易知f(x)在(0,+∞)上为增函数,
又f(10-2a)<f(a+1),
所以解得
所以3<a≤5.
13.已知幂函数y=f(x)=x-2m2-m+3,其中m∈{m|-2<m<2,m∈Z},满足:
(1)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(-x)+f(x)=0.求同时满足(1),(2)的幂函数f(x)的解析式,并求x∈[0,3]时f(x)的值域.
解 因为m∈{m|-2<m<2,m∈Z},所以m=-1,0,1.因为对任意x∈R,都有f(-x)+f(x)=0,即f(-x)=-f(x),所以f(x)是奇函数.
当m=-1时,f(x)=x2只满足条件(1)而不满足条件(2);
当m=1时,f(x)=x0条件(1),(2)都不满足.
当m=0时,f(x)=x3条件(1),(2)都满足,且在区间[0,3]上是增函数,f(0)=03=0,f(3)=33=27,所以x∈[0,3]时,函数f(x)的值域为[0,27].
三、创新拓展
14.(多选)已知幂函数y=xm2-2m-3(m∈Z)的图象与x轴和y轴没有交点,且关于y轴对称,则m可等于( )
A.-1 B.0
C.1 D.3
答案 ACD
解析 ∵幂函数y=xm2-2m-3(m∈Z)的图象与x轴、y轴没有交点,且关于y轴对称,
∴m2-2m-3≤0,且m2-2m-3(m∈Z)为偶数,
由m2-2m-3≤0,得-1≤m≤3,
又m∈Z,∴m=-1,0,1,2,3.
当m=-1时,m2-2m-3=1+2-3=0,为偶数,符合题意;
当m=0时,m2-2m-3=-3,为奇数,不符合题意;
当m=1时,m2-2m-3=1-2-3=-4,为偶数,符合题意;
当m=2时,m2-2m-3=4-4-3=-3,为奇数,不符合题意;
当m=3时,m2-2m-3=9-6-3=0,为偶数,符合题意.
高中数学湘教版(2019)必修 第一册3.1 函数优秀习题ppt课件: 这是一份高中数学湘教版(2019)必修 第一册3.1 函数优秀习题ppt课件,文件包含培优课幂函数单调性的常见应用doc、培优课幂函数单调性的常见应用pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
必修 第一册3.1 函数精品习题ppt课件: 这是一份必修 第一册3.1 函数精品习题ppt课件,文件包含限时小练27幂函数doc、限时小练27幂函数pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
高中数学湘教版(2019)必修 第一册5.1 任意角与弧度制完美版课件ppt: 这是一份高中数学湘教版(2019)必修 第一册5.1 任意角与弧度制完美版课件ppt,文件包含512弧度制doc、512弧度制pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。













