2021年黑龙江省双鸭山市宝清县中考数学一模试卷(含答案)

这是一份2021年黑龙江省双鸭山市宝清县中考数学一模试卷(含答案)，共32页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2021年黑龙江省双鸭山市宝清县中考数学一模试卷
一、选择题（每小题3分，共30分）
1．（3分）下列运算正确的是（　　）
A．a2•a3＝a6 B．a8÷a4＝a2
C．5a﹣3a＝2a D．（﹣ab2）2＝﹣a2b4
2．（3分）下列垃圾分类标识图案，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
3．（3分）如果点P（m，1+2m）在第二象限，那么m的取值范围是（　　）
A． B． C．m＜0 D．
4．（3分）如图，已知▱ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC＝60°，∠ADA′＝50°，则∠DA′E′的大小为（　　）

A．130° B．150° C．160° D．170°
5．（3分）某校足球队有16名队员，队员的年龄情况统计如下：
年龄/岁
13
14
15
16
人数
3
5
6
2
则这16名队员年龄的中位数和众数分别是（　　）
A．14，15 B．15，15 C．14.5，14 D．14.5，15
6．（3分）为了美化环境，我县加大对绿化的投资，2016年用于绿化的投资为20万元，2018年用于绿化的投资为25万元，求这两年绿化投资的年平均增长率．设这两年绿化投资的年平均增长率为x，根据题意，所列方程为（　　）
A．20x2＝25 B．20（1+x）＝25
C．20（1+x）2＝25 D．20（1+x）+20（1+x）2＝25
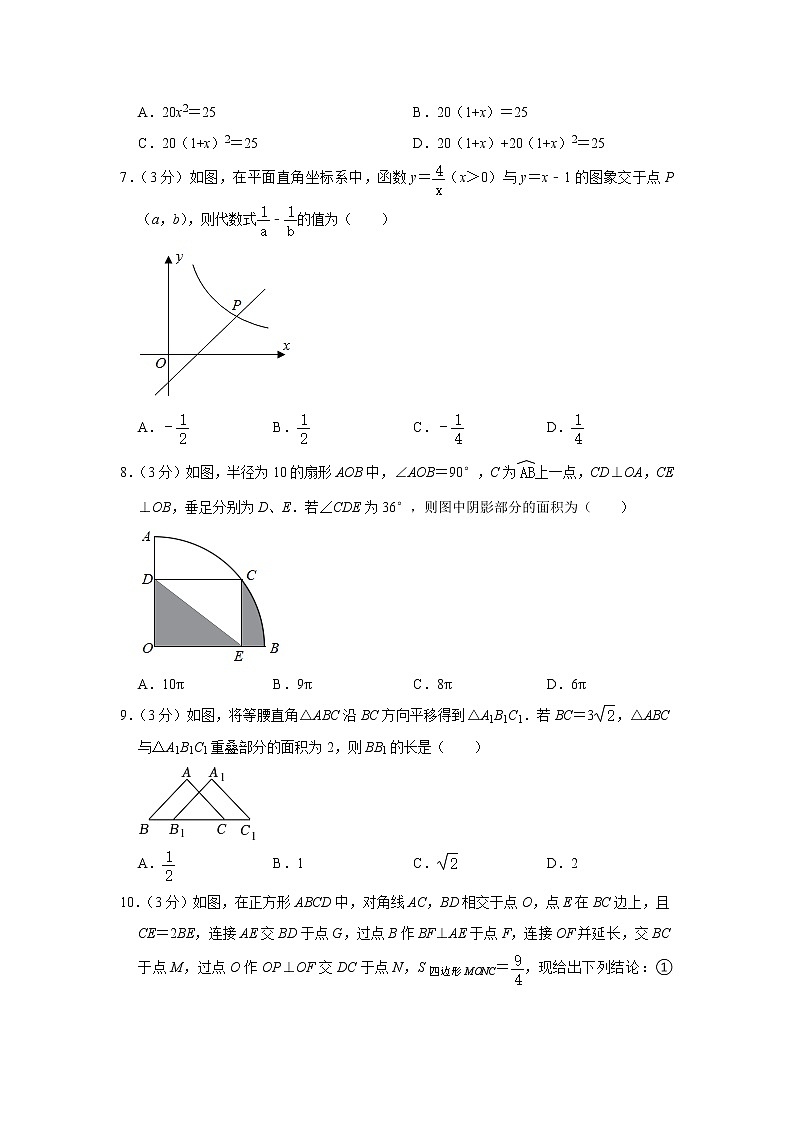
7．（3分）如图，在平面直角坐标系中，函数y＝（x＞0）与y＝x﹣1的图象交于点P（a，b），则代数式﹣的值为（　　）

A．﹣ B． C．﹣ D．
8．（3分）如图，半径为10的扇形AOB中，∠AOB＝90°，C为上一点，CD⊥OA，CE⊥OB，垂足分别为D、E．若∠CDE为36°，则图中阴影部分的面积为（　　）

A．10π B．9π C．8π D．6π
9．（3分）如图，将等腰直角△ABC沿BC方向平移得到△A1B1C1．若BC＝3，△ABC与△A1B1C1重叠部分的面积为2，则BB1的长是（　　）

A． B．1 C． D．2
10．（3分）如图，在正方形ABCD中，对角线AC，BD相交于点O，点E在BC边上，且CE＝2BE，连接AE交BD于点G，过点B作BF⊥AE于点F，连接OF并延长，交BC于点M，过点O作OP⊥OF交DC于点N，S四边形MONC＝，现给出下列结论：①；②sin∠BOF＝；③OF＝；④OG＝BG；其中正确的结论有（　　）

A．①②③ B．②③④ C．①②④ D．①③④
二、填空题（每小题3分，共30分）
11．（3分）2019年1月1日，“学习强国”平台全国上线，截至2019年3月17日，某市党员“学习强国”客户端注册人数约1180000，将数据1180000用科学记数法表示为　 　．
12．（3分）代数式有意义，则x的取值范围是 　 　．
13．（3分）某商品每件的标价是330元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为　 　元．
14．（3分）如图，▱ABCD中，∠ADC＝119°，BE⊥DC于点E，DF⊥BC于点F，BE与DF交于点H，则∠BHF＝　 　度．

15．（3分）如图，在⊙O中，弦AB＝1，点C在AB上移动，连接OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为　 　．

16．（3分）若关于x的方程+＝无解，则m的值为　 　．
17．（3分）如图，D是等边三角形ABC外一点．若BD＝8，CD＝6，连接AD，则AD的最大值与最小值的差为 　 　．

18．（3分）一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中有 　 　个白球．
19．（3分）某校三个绿化小组一天植树的棵数如下：10，x，8，已知这组数据只有一个众数且众数等于中位数，那么这组数据的平均数是　 　．
20．（3分）如图，在矩形OAA1B中，OA＝3，AA1＝2，连接OA1，以OA1为边，作矩形OA1A2B1使A1A2＝OA1，连接OA2交A1B于点C；以OA2为边，作矩形OA2A3B2，使A2A3＝OA2，连接OA3交A2B1于点C1；以OA3为边，作矩形OA3A4B3，使A3A4＝OA3，连接OA4交A3B2于点C2；…按照这个规律进行下去，则△C2019C2020A2022的面积为　 　．

三、解答题（满分60分）
21．（5分）化简求值：（﹣）÷，当a＝﹣1时，请你选择一个适当的数作为b的值，代入求值．
22．（6分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，O、M也在格点上．
（1）画出△ABC关于直线OM对称的△A1B1C1；
（2）画出△ABC绕点O按顺时针方向旋转90°后所得的△A2B2C2；
（3）△A1B1C1与△A2B2C2组成的图形是轴对称图形吗？如果是轴对称图形，请画出对称轴．

23．（6分）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx﹣2（a≠0）与x轴交于A（1，0），B（3，0）两点，与y轴交于点C，其顶点为点D，点E的坐标为（0，﹣1），该抛物线与BE交于另一点F，连接BC．
（1）求该抛物线的解析式，并用配方法把解析式化为y＝a（x﹣h）2+k的形式；
（2）若点H（1，y）在BC上，连接FH，求△FHB的面积．

24．（7分）学生的学习兴趣如何是每位教师非常关注的问题．为此，某校教师对该校部分学生的学习兴趣进行了一次抽样调查（把学生的学习兴趣分为三个层次，A层次：很感兴趣；B层次：较感兴趣；C层次：不感兴趣）；并将调查结果绘制成了图①和图②的统计图（不完整）．请你根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了　 　名学生；
（2）图①、②补充完整；
（3）将图②中C层次所在扇形的圆心角的度数；
（4）根据抽样调查的结果，请你估计该校1200名学生中大约有多少名学生对学习感兴趣（包括A层次和B层次）．

25．（8分）甲、乙二人骑自行车同时从张庄出发，沿同一路线去李庄．甲行驶20分钟因事耽误一会儿，事后继续按原速行驶．如图表示甲、乙二人骑自行车行驶的路程y（千米）随时间x（分）变化的图象（全程），根据图象回答下列问题：
（1）乙比甲晚多长时间到达李庄？
（2）甲因事耽误了多长时间？
（3）x为何值时，乙行驶的路程比甲行驶的路程多1千米？

26．（8分）在△ABC中，AB＝BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．
（1）如图1，请直接写出线段OE与OF的数量关系；
（2）如图2，当∠ABC＝90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由
（3）若|CF﹣AE|＝2，EF＝2，当△POF为等腰三角形时，请直接写出线段OP的长．

27．（10分）某中学为落实市教育局提出的“全员育人，创办特色学校”的会议精神，决心打造“书香校园”，计划用不超过1900本科技类书籍和1620本人文类书籍，组建中、小型两类图书角共30个．已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．
（1）符合题意的组建方案有几种？请你帮学校设计出来；
（2）若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570元，试说明（1）中哪种方案费用最低，最低费用是多少元？
28．（10分）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12＝0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
（1）求A、B两点的坐标．
（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．
（3）当t＝2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．


2021年黑龙江省双鸭山市宝清县中考数学一模试卷
（参考答案与详解）
一、选择题（每小题3分，共30分）
1．（3分）下列运算正确的是（　　）
A．a2•a3＝a6 B．a8÷a4＝a2
C．5a﹣3a＝2a D．（﹣ab2）2＝﹣a2b4
【解答】解：（A）原式＝a5，故A错误．
（B）原式＝a4，故B错误．
（D）原式＝a2b4，故D错误．
故选：C．
2．（3分）下列垃圾分类标识图案，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【解答】解：A、不是中心对称图形，不是轴对称图形，故此选项不合题意；
B、不是中心对称图形，是轴对称图形，故此选项不合题意；
C、既是中心对称图形，也是轴对称图形，故此选项符合题意；
D、不是中心对称图形，不是轴对称图形，故此选项不合题意；
故选：C．
3．（3分）如果点P（m，1+2m）在第二象限，那么m的取值范围是（　　）
A． B． C．m＜0 D．
【解答】解：∵点P（m，1+2m）在第二象限，
∴，
解得．
故选：B．
4．（3分）如图，已知▱ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC＝60°，∠ADA′＝50°，则∠DA′E′的大小为（　　）

A．130° B．150° C．160° D．170°
【解答】解：∵四边形ABCD是平行四边形，∠ADC＝60°，
∴∠ABC＝60°，∠DCB＝120°，
∵∠ADA′＝50°，
∴∠A′DC＝10°，
∴∠DA′B＝130°，
∵AE⊥BC于点E，
∴∠BAE＝30°，
∵△BAE顺时针旋转，得到△BA′E′，
∴∠BA′E′＝∠BAE＝30°，
∴∠DA′E′＝∠DA′B+∠BA′E′＝160°．
故选：C．
5．（3分）某校足球队有16名队员，队员的年龄情况统计如下：
年龄/岁
13
14
15
16
人数
3
5
6
2
则这16名队员年龄的中位数和众数分别是（　　）
A．14，15 B．15，15 C．14.5，14 D．14.5，15
【解答】解：共有16个数，最中间两个数的平均数是（14+15）÷2＝14.5，则中位数是14.5；
15出现了6次，出现的次数最多，则众数是15；
故选：D．
6．（3分）为了美化环境，我县加大对绿化的投资，2016年用于绿化的投资为20万元，2018年用于绿化的投资为25万元，求这两年绿化投资的年平均增长率．设这两年绿化投资的年平均增长率为x，根据题意，所列方程为（　　）
A．20x2＝25 B．20（1+x）＝25
C．20（1+x）2＝25 D．20（1+x）+20（1+x）2＝25
【解答】解：设这两年绿化投资的年平均增长率为x，那么依题意得：
20（1+x）2＝25
故选：C．
7．（3分）如图，在平面直角坐标系中，函数y＝（x＞0）与y＝x﹣1的图象交于点P（a，b），则代数式﹣的值为（　　）

A．﹣ B． C．﹣ D．
【解答】解：
法一：由题意得，
，解得，或（舍去），
∴点P（，），
即：a＝，b＝，
∴﹣＝﹣＝﹣；
法二：由题意得，
函数y＝（x＞0）与y＝x﹣1的图象交于点P（a，b），
∴ab＝4，b＝a﹣1，
∴﹣＝＝；
故选：C．
8．（3分）如图，半径为10的扇形AOB中，∠AOB＝90°，C为上一点，CD⊥OA，CE⊥OB，垂足分别为D、E．若∠CDE为36°，则图中阴影部分的面积为（　　）

A．10π B．9π C．8π D．6π
【解答】解：连接OC，
∵∠AOB＝90°，CD⊥OA，CE⊥OB，
∴四边形CDOE是矩形，
∴CD∥OE，
∴∠DEO＝∠CDE＝36°，
由矩形CDOE易得到△DOE≌△CEO，
∴∠COB＝∠DEO＝36°
∴图中阴影部分的面积＝扇形OBC的面积，
∵S扇形OBC＝＝10π
∴图中阴影部分的面积＝10π，
故选：A．

9．（3分）如图，将等腰直角△ABC沿BC方向平移得到△A1B1C1．若BC＝3，△ABC与△A1B1C1重叠部分的面积为2，则BB1的长是（　　）

A． B．1 C． D．2
【解答】解：设B1C＝2x，
根据等腰三角形的性质可知，重叠部分为等腰直角三角形
则B1C边上的高为x，
∴×x×2x＝2，解得x＝（舍去负值），
∴B1C＝2，
∴BB1＝BC﹣B1C＝．
故选：C．
10．（3分）如图，在正方形ABCD中，对角线AC，BD相交于点O，点E在BC边上，且CE＝2BE，连接AE交BD于点G，过点B作BF⊥AE于点F，连接OF并延长，交BC于点M，过点O作OP⊥OF交DC于点N，S四边形MONC＝，现给出下列结论：①；②sin∠BOF＝；③OF＝；④OG＝BG；其中正确的结论有（　　）

A．①②③ B．②③④ C．①②④ D．①③④
【解答】解：如图，过点O作OH∥BC交AE于点H，过点O作OQ⊥BC交BC于点Q，过点B作BK⊥OM交OM的延长线于点K，

∵四边形ABCD是正方形，
∴，
∴OB＝OC，∠BOC＝90°，
∴∠BOM+∠MOC＝90°．
∵OP⊥OF，
∴∠MON＝90°，
∴∠CON+∠MOC＝90°，
∴∠BOM＝∠CON，
∴△BOM≌△CON（ASA），
∴S△BOM＝S△CON，
∴，
∴，
∴．
∵CE＝2BE，
∴，
∴．
∵BF⊥AE，
∴，
∴，
∴，
∴，
∴，
∴，
∴BM＝，MQ＝．
∵AD∥BC，
∴，故①正确；
∵OH∥BC，
∴，
又∵CE＝2BE，
∴OH＝BE，AH＝HE＝．
∵∠HGO＝∠EGB，
∴△HOG≌△EBG（AAS），
∴OG＝BG，故④正确；
∵OQ2+MQ2＝OM2，
∴，
∴，故③正确；
∵，
即，
∴，
∴，故②错误；
∴正确的有①③④．
故选：D．
二、填空题（每小题3分，共30分）
11．（3分）2019年1月1日，“学习强国”平台全国上线，截至2019年3月17日，某市党员“学习强国”客户端注册人数约1180000，将数据1180000用科学记数法表示为　1.18×106　．
【解答】解：1180000＝1.18×106，
故答案为：1.18×106．
12．（3分）代数式有意义，则x的取值范围是 　x≥3　．
【解答】解：根据二次根式有意义，分式有意义得x﹣3≥0且x﹣2≠0，
解得：x≥3．
故答案为：x≥3．
13．（3分）某商品每件的标价是330元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为　240　元．
【解答】解：设这种商品每件的进价为x元，
根据题意得：330×80%﹣x＝10%x，
解得：x＝240，
则这种商品每件的进价为240元．
故答案为：240
14．（3分）如图，▱ABCD中，∠ADC＝119°，BE⊥DC于点E，DF⊥BC于点F，BE与DF交于点H，则∠BHF＝　61　度．

【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，DC∥AB，
∵∠ADC＝119°，DF⊥BC，
∴∠ADF＝90°，
则∠EDH＝29°，
∵BE⊥DC，
∴∠DEH＝90°，
∴∠DHE＝∠BHF＝90°﹣29°＝61°．
故答案为：61．
15．（3分）如图，在⊙O中，弦AB＝1，点C在AB上移动，连接OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为　　．

【解答】解：连接OD，如图，
∵CD⊥OC，
∴∠DCO＝90°，
∴CD＝＝，
当OC的值最小时，CD的值最大，
而OC⊥AB时，OC最小，此时D、B两点重合，
∴CD＝CB＝AB＝×1＝，
即CD的最大值为，
故答案为：．
16．（3分）若关于x的方程+＝无解，则m的值为　﹣1或5或﹣　．
【解答】解：去分母得：x+4+m（x﹣4）＝m+3，
可得：（m+1）x＝5m﹣1，
当m+1＝0时，一元一次方程无解，
此时m＝﹣1，
当m+1≠0时，
则x＝＝±4，
解得：m＝5或﹣，
综上所述：m＝﹣1或5或﹣，
故答案为：﹣1或5或﹣．
17．（3分）如图，D是等边三角形ABC外一点．若BD＝8，CD＝6，连接AD，则AD的最大值与最小值的差为 　12　．

【解答】解：如图，以CD为边向外作等边△CDE，连接BE，

∵△CDE和△ABC是等边三角形，
∴CE＝CD，CB＝CA，∠ECD＝∠BCA＝60°，
∴∠ECB＝∠DCA，
在△ECB和△DCA中，，
∴△ECB≌△DCA（SAS），
∴BE＝AD，
∵DE＝CD＝6，BD＝8，
∴BD﹣DE≤BE≤BD+DE，
即8﹣6≤BE≤8+6，
∴2≤BE≤14，
∴2≤AD≤14．
则当B、D、E三点共线时，如图所示：

可得BE的最大值与最小值分别为14和2．
∴AD的最大值与最小值的差为14﹣2＝12．
故答案为：12．
18．（3分）一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中有 　3　个白球．
【解答】解：由题意可得，红球的概率为70%．则白球的概率为30%，
这个口袋中白球的个数：10×30%＝3（个），
故答案为3．
19．（3分）某校三个绿化小组一天植树的棵数如下：10，x，8，已知这组数据只有一个众数且众数等于中位数，那么这组数据的平均数是　或　．
【解答】解：因为这组数据只有一个众数且众数等于中位数，
所以x＝10或8，
那么这组数据的平均数是×（10+10+8）＝，或×（10+8+8）＝．
故填或．
20．（3分）如图，在矩形OAA1B中，OA＝3，AA1＝2，连接OA1，以OA1为边，作矩形OA1A2B1使A1A2＝OA1，连接OA2交A1B于点C；以OA2为边，作矩形OA2A3B2，使A2A3＝OA2，连接OA3交A2B1于点C1；以OA3为边，作矩形OA3A4B3，使A3A4＝OA3，连接OA4交A3B2于点C2；…按照这个规律进行下去，则△C2019C2020A2022的面积为　　．

【解答】解：在矩形OAA1B中，∵OA＝3，AA1＝2，
∴∠A＝90°，
∴OA1＝＝＝，
∵＝＝，
∴＝，
∵∠OA1A2＝∠A＝90°，
∴△OA1A2∽△OAA1，
∴∠A1OA2＝∠AOA1，
∵A1B∥OA，
∴∠CA1O＝∠AOA1，
∴∠COA1＝∠CA1O，
∴OC＝CA1，
∵∠A2OA1+∠OA2A1＝90°，∠OA1C+∠A2A1C＝90°，
∴∠CA2A1＝∠CA1A2，
∴CA1＝CA2＝OC，
同法可证OC1＝A3C1，
∴CC1∥A2A3，CC1＝A2A3，
∴＝，
∵A1A2＝，
∴OA2＝＝＝，
∴A2A3＝×＝，
∴CC1＝A2A3＝，
∴＝＝××＝，
同法可证＝S，
由题意，＝＝＝，
∵△C2A3C1∽△C1A2C，
∴相似比为：＝，
∴＝（）2×＝，＝，…，
由此规律可得，△C2019C2020A2022的面积为．
故答案为．

三、解答题（满分60分）
21．（5分）化简求值：（﹣）÷，当a＝﹣1时，请你选择一个适当的数作为b的值，代入求值．
【解答】解：原式＝•
＝•
＝，
当a＝﹣1，b＝0（注意b不能为1或﹣1）时，原式＝﹣1．
22．（6分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，O、M也在格点上．
（1）画出△ABC关于直线OM对称的△A1B1C1；
（2）画出△ABC绕点O按顺时针方向旋转90°后所得的△A2B2C2；
（3）△A1B1C1与△A2B2C2组成的图形是轴对称图形吗？如果是轴对称图形，请画出对称轴．

【解答】解：（1）如图所示，对称图形正确给2分；

（2）如图所示，旋转正确给2分；

（3）如图所示，对称轴每一条正确给1分，共2分．

23．（6分）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx﹣2（a≠0）与x轴交于A（1，0），B（3，0）两点，与y轴交于点C，其顶点为点D，点E的坐标为（0，﹣1），该抛物线与BE交于另一点F，连接BC．
（1）求该抛物线的解析式，并用配方法把解析式化为y＝a（x﹣h）2+k的形式；
（2）若点H（1，y）在BC上，连接FH，求△FHB的面积．

【解答】解：（1）∵抛物线y＝ax2+bx﹣2（a≠0）与x轴交于A（1，0）、B（3，0）两点，
∴，
解得a＝﹣，b＝，
∴抛物线解析式为y＝﹣x2+x﹣2＝﹣（x﹣2）2+；
（2）过A作y轴的平行线，交BC于H，交BE于G，
由（1）有：C（0，﹣2），
∵B（3，0），
∴BC所在直线解析式：y＝x﹣2，
∵H（1，y）在BC上，
∴y＝×1﹣2＝﹣，
∴H（1，﹣），
∵B（3，0），E（0，﹣1），
∴BE所在直线解析式：y＝x﹣1，
∴G（1，﹣），
∴GH＝﹣﹣（﹣）＝，
∵直线BE：y＝x﹣1与抛物线：y＝﹣x2+x﹣2交于F，B两点，
∴F（，﹣），
∴S△FHB＝GH×（xG﹣xF）+CH×（xB﹣xG）
＝GH×（xB﹣xF）
＝××（3﹣）
＝．

24．（7分）学生的学习兴趣如何是每位教师非常关注的问题．为此，某校教师对该校部分学生的学习兴趣进行了一次抽样调查（把学生的学习兴趣分为三个层次，A层次：很感兴趣；B层次：较感兴趣；C层次：不感兴趣）；并将调查结果绘制成了图①和图②的统计图（不完整）．请你根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了　200　名学生；
（2）图①、②补充完整；
（3）将图②中C层次所在扇形的圆心角的度数；
（4）根据抽样调查的结果，请你估计该校1200名学生中大约有多少名学生对学习感兴趣（包括A层次和B层次）．

【解答】解：（1）此次抽样调查中，共调查了
50÷25%＝200（名）；
故答案为：200．

（2）C层次的人数为：200﹣120﹣50＝30（人）；
所占的百分比是：×100%＝15%；
B层次的人数所占的百分比是1﹣25%﹣15%＝60%；

（3）C层次所在扇形的圆心角的度数是：360×15%＝54°；

（4）根据题意得：
（25%+60%）×1200＝1020（名）
答：估计该校1200名学生中大约有1020名学生对学习感兴趣．

25．（8分）甲、乙二人骑自行车同时从张庄出发，沿同一路线去李庄．甲行驶20分钟因事耽误一会儿，事后继续按原速行驶．如图表示甲、乙二人骑自行车行驶的路程y（千米）随时间x（分）变化的图象（全程），根据图象回答下列问题：
（1）乙比甲晚多长时间到达李庄？
（2）甲因事耽误了多长时间？
（3）x为何值时，乙行驶的路程比甲行驶的路程多1千米？

【解答】解：（1）设直线OD解析式为y＝k1x（k1≠0），
由题意可得60k1＝10，，
当y＝15时，，x＝90，90﹣80＝10分
故乙比甲晚10分钟到达李庄．
（2）设直线BC解析式为y＝k2x+b（k2≠0），
由题意可得
解得∴y＝x﹣5
由图象可知甲20分钟行驶的路程为5千米，x﹣5＝5，x＝40，40﹣20＝20分
故甲因事耽误了20分钟．
（3）分两种情况：
①，解得：x＝36
②x﹣（x﹣5）＝1，解得：x＝48
当x为36或48时，乙行驶的路程比甲行驶的路程多1千米．
26．（8分）在△ABC中，AB＝BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．
（1）如图1，请直接写出线段OE与OF的数量关系；
（2）如图2，当∠ABC＝90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由
（3）若|CF﹣AE|＝2，EF＝2，当△POF为等腰三角形时，请直接写出线段OP的长．

【解答】解：（1）如图1中，延长EO交CF于K．

∵AE⊥BE，CF⊥BE，
∴AE∥CK，
∴∠EAO＝∠KCO，
∵OA＝OC，∠AOE＝∠COK，
∴△AOE≌△COK，
∴OE＝OK，
∵△EFK是直角三角形，
∴OF＝EK＝OE．

（2）如图2中，延长EO交CF于K．

∵∠ABC＝∠AEB＝∠CFB＝90°，
∴∠ABE+∠BAE＝90°，∠ABE+∠CBF＝90°，
∴∠BAE＝∠CBF，
∵AB＝BC，
∴△ABE≌△BCF，
∴BE＝CF，AE＝BF，
∵△AOE≌△COK，
∴AE＝CK，OE＝OK，
∴FK＝EF，
∴△EFK是等腰直角三角形，
∴OF⊥EK，OF＝OE．

（3）如图3中，延长EO交CF于K．作PH⊥OF于H．

∵|CF﹣AE|＝2，EF＝2，AE＝CK，
∴FK＝2，
在Rt△EFK中，tan∠FEK＝，
∴∠FEK＝30°，∠EKF＝60°，
∴EK＝2FK＝4，OF＝EK＝2，
∵△OPF是等腰三角形，观察图形可知，只有OF＝FP＝2，
在Rt△PHF中，PH＝PF＝1，HF＝，OH＝2﹣，
∴OP＝＝﹣

如图4中，当点P在线段OC上时，作PG⊥OF于G．

同法可得：HE＝2，OH＝OF，EF＝2，
∴tan∠HFE＝，
∴∠HFE＝30°，
∴FH＝2HE＝4，
∵OH＝OF，
∴OH＝OF＝OE＝2，
∵△OPF的等腰三角形，
∴PO＝PF，
∵PG⊥OF，
∴OG＝GF＝1，
∴OP＝＝
综上所述，OP的长为﹣或．
27．（10分）某中学为落实市教育局提出的“全员育人，创办特色学校”的会议精神，决心打造“书香校园”，计划用不超过1900本科技类书籍和1620本人文类书籍，组建中、小型两类图书角共30个．已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．
（1）符合题意的组建方案有几种？请你帮学校设计出来；
（2）若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570元，试说明（1）中哪种方案费用最低，最低费用是多少元？
【解答】解：（1）设组建中型图书角x个，则组建小型图书角为（30﹣x）个．
由题意，得，
化简得，
解这个不等式组，得18≤x≤20．
由于x只能取整数，∴x的取值是18，19，20．
当x＝18时，30﹣x＝12；当x＝19时，30﹣x＝11；当x＝20时，30﹣x＝10．
故有三种组建方案：
方案一，中型图书角18个，小型图书角12个；
方案二，中型图书角19个，小型图书角11个；
方案三，中型图书角20个，小型图书角10个．

（2）方案一的费用是：860×18+570×12＝22320（元）；
方案二的费用是：860×19+570×11＝22610（元）；
方案三的费用是：860×20+570×10＝22900（元）．
故方案一费用最低，最低费用是22320元．
28．（10分）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12＝0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
（1）求A、B两点的坐标．
（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．
（3）当t＝2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．

【解答】解：（1）解方程x2﹣7x+12＝0，得x1＝3，x2＝4，
∵OA＜OB，∴OA＝3，OB＝4．
∴A（0，3），B（4，0）．

（2）在Rt△AOB中，OA＝3，OB＝4，
∴AB＝5，
∴AP＝t，QB＝2t，AQ＝5﹣2t．
△APQ与△AOB相似，可能有两种情况：
①△APQ∽△AOB，如图（2）a所示．
则有，即，解得t＝．
此时OP＝OA﹣AP＝，PQ＝AP•tanA＝，
∴Q（，）；
②△APQ∽△ABO，如图（2）b所示．
则有，即，解得t＝．
此时AQ＝，AH＝AQ•cosA＝，HQ＝AQ•sinA＝，OH＝OA﹣AH＝，
∴Q（，）．
综上所述，当t＝秒或t＝秒时，△APQ与△AOB相似，所对应的Q点坐标分别为（，）或（，）．

（3）结论：存在．如图（3）所示．
∵t＝2，∴AP＝2，AQ＝1，OP＝1．
过Q点作QE⊥y轴于点E，则QE＝AQ•sin∠QAP＝，AE＝AQ•cos∠QAP＝，
∴OE＝OA﹣AE＝，
∴Q（，）．
∵▱APM1Q，
∴QM1⊥x轴，且QM1＝AP＝2，
∴M1（，）；
∵▱APQM2，
∴QM2⊥x轴，且QM2＝AP＝2，
∴M2（，）；
如图（3），过M3点作M3F⊥y轴于点F，
∵▱AQPM3，
∴M3P＝AQ，∠QAE＝∠M3PF，
∴∠PM3F＝∠AQE；
在△M3PF与△QAE中，
∵∠QAE＝∠M3PF，M3P＝AQ，∠PM3F＝∠AQE，
∴△M3PF≌△QAE，
∴M3F＝QE＝，PF＝AE＝，
∴OF＝OP+PF＝，
∴M3（﹣，）．
∴当t＝2时，在坐标平面内，存在点M，使以A、P、Q、M为顶点的四边形是平行四边形．
点M的坐标为：M1（，），M2（，），M3（﹣，）．