




2023年中考数学二轮复习必会几何模型剖析--3.4 “半角”模型(旋转)(全等模型)(精品课件)
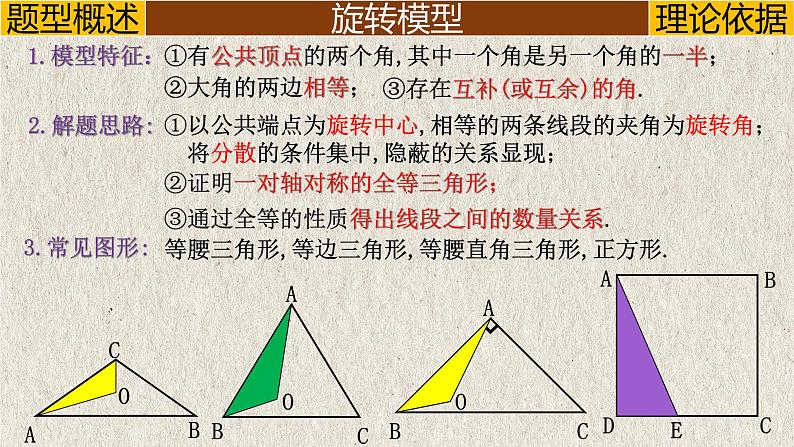
展开①有公共顶点的两个角,其中一个角是另一个角的一半;
③存在互补(或互余)的角.
③通过全等的性质得出线段之间的数量关系.
①以公共端点为旋转中心,相等的两条线段的夹角为旋转角; 将分散的条件集中,隐蔽的关系显现;
②证明一对轴对称的全等三角形;
等腰三角形,等边三角形,等腰直角三角形,正方形.
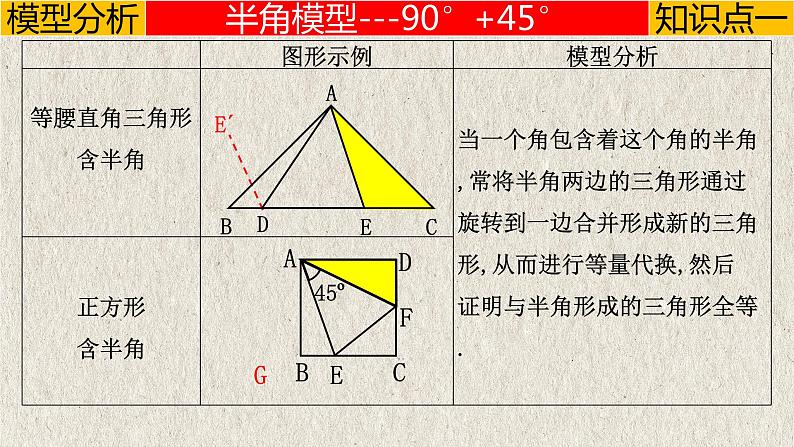
半角模型---90°+45°
半角模型---120°+60°
半角模型---邻补四边形
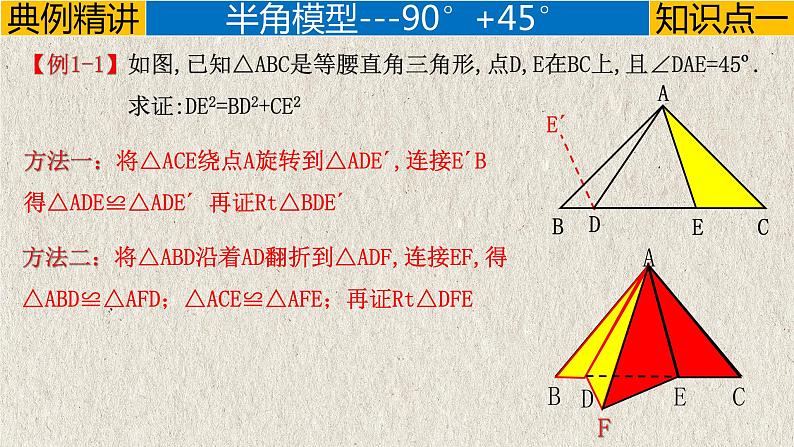
【例1-1】如图,已知△ABC是等腰直角三角形,点D,E在BC上,且∠DAE=45º. 求证:DE2=BD2+CE2
方法一:将△ACE绕点A旋转到△ADE´,连接E´B得△ADE≌△ADE´ 再证Rt△BDE´
方法二:将△ABD沿着AD翻折到△ADF,连接EF,得△ABD≌△AFD;△ACE≌△AFE;再证Rt△DFE
【例1-2】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º.求证:EF=DF+BE;
【分析】将△ABE绕点A逆时针旋转90º得△ADE´.
易证:AE´=AE,BE=DE´,∠E´AF=45º
易证:△AFE´≌△AFE(SAS)→EF=E´F
∴EF=E´F=DF+DE´=DF+BE.
将△ABE绕点A逆时针旋转90º得△ADE´.
∴△AEF≌△AE´F.(SAS)
证明:∵四边形ABCD正方形.
∴BC=CD=DA=AB,∠BAD=∠B=∠ADC=90º.
∴∠ADE´=∠B=90º,∠E´AD=BAE,AE´=AE,DE´=BE,
∵∠EAF=45º,∠BAD=90º.
∴∠BAE+∠DAF=45º.
∴∠E´AF=∠E´AD+∠DAF=∠BAE+∠DAF=45º.
∴EF=E´F=DF+BE
【例1-2】如图,若E,F分别在CB,DC延长线上时,∠EAF=45º.EF=DF+BE还成立吗?若成立,请证明.若不成立,写出新的结论,并证明.
∴EF=E´F=DF-DE´=DF-BE.
【变式1】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º.求证:C△CEF=2BC;
∴C△CEF=CF+EF+CE
=CF+DF+BE+CE
易证:EF=E´F=DF+DE´=DF+BE.
【变式2】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于点M,N.求证:BM2+DN2=MN2
【分析】将△ADN绕点A顺时针旋转90º得△AMN´,连接MN´
易证:AN´=AN,DN=BN´,∠N´BA=∠NDA=45º,∠N´AM=45º
易证:△AMN´≌△AMN(SAS)→MN=MN´,∠N´BM=90º
易证:BN´2+BM2=MN´2.
∴BM2+DN2=MN2
【变式3】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于点M,N,过点A作AH⊥EF于点H,求证:(1)△ABE≌△AHE;△AHF≌△ADF; (2)EA平分∠BEF,FA平分∠DFE.
【变式4】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于点M,N.求证:(1)A、B、E、N四点共圆; (2)A、D、F、M四点共圆; (3)M、N、F、E四点共圆.
(1)∵∠EAN=∠EBN=45º,∴A、B、E、N四点共圆
(2)∵∠FAM=∠FBM=45º,∴A、D、F、M四点共圆
(3)∵∠MEN=∠MFN=45º,∴M、N、F、E四点共圆
(1)∵∠MEN=∠MFN=45º,∴M、N、F、E四点共圆
∴∠ANM=∠AEF,∠AMN=∠AFE,
∴△AMN∽△AFE.
【变式6】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于点M,N,求证:(1)△MAN∽△MDA;(2)△NAM∽△NBA.
(1)∴∠AMN=∠AMN,∠MAN=∠ADM=45º,
∴△MAN∽△MDA.
(2)∴∠ANM=∠ANM,∠MAN=∠ABN=45º,
∴△NAM∽△NBA.
【变式7】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于点M,N,求证:(1)△AMB∽△AFC;(2)△AND∽△AEC;
如图:正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,连接BD交AE于G,AF于M,连接EM、GF.GF与EM相交于O点.则有下列结论.
②GB2+MD2=GM2
④AM=EM,AG=FG
⑦△AEF的边EF上的高等于正方形的边长;
⑧△EFC的周长等于正方形的边长的2倍.
①∠AEB=∠AEF,∠AFE=∠AFD
②根据下面共圆,每个共圆都至少可以得到四队相等的角.
△AGF与△AME是等腰直角三角形
①S△AEF=S△ABE+S△ADF
②S△AEF=2S△AGM
③S正方形ABCD:S△AEF=2AB:EF
①△AEF∽△AMG∽△BGE∽△DMF∽△DAG∽△MBA
【例2】如图,△ABC是等边三角形,BD=CD且∠BDC=120º,E、F在边AB、AC上且∠EDF=60º.求证:EF=BE+CF.
【分析】将△BDN绕点D顺时针旋转120º得△DCG,
易证:△DBE≌△DCG(SAS)→DE=DG,∠FDG=∠FDE=60º
易证:△DFE≌△DFG(SAS)→EF=GF,
∴EF=GF=GC+CF=BE+CF
如图,△ABC是等边三角形,BD=CD且∠BDC=120º,E在直线AB上,点F在AC的延长线上,且∠EDF=60º.试问EF、BE、CF之间又有何数量关系?
先将△ABE绕点A旋转得△ADE´再证△AEF≌△AE´F结论:EF=BE-DF
【例3】如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180º,E,F分别是BC,CD上的点,且∠EAF=0.5∠BAD,BE,DF,EF三条线段之间的数量关系是否仍然成立,若不成立,写出它们之间的数量关系并证明.
半角信息——带形旋转——轴对称的全等三角形.
邻补四边形内含半角(邻边相等,对角互补的四边形)
1.如图:四边形ABCD中,E、F分别是CD、AD上的点,∠ABC= ∠ADC=90º且∠EBF=45º.猜想并证明线段EF、CE、AF之间的数量关系.
2.如图:四边形ABCD中,E、F分别是CD、AD上的点, ∠ABC+∠ADC=180º且∠EBF=1/2∠ABCº.猜想并证明线段EF、CE、AF之间的数量关系.
2.如图:等腰直角△ABC中,∠ABC =90º,E、F都是AC上的点,且∠EBF=45º,猜想并证明线段EF、CE、AF之间的数量关系.
备注:用旋转法和截长补短法两种方法证明.
说明:上图依次是45º,30º的三角形对称(翻折),翻折形成正方形或等边三角形等的对称全等.(半角可以任意角去折叠,常见度数还有22.5º半角)
说明:轴对称有如下性质:
①把图形变为与之全等的图形,因而面积和周长不变.
②在反射变换下,任意两点A和B,变换后的对应点为A´和B´,则有直线AB和A´B´所成的角的平分线为l.
③两点之间的距离保持不变,任意两点A和B,变换后的对应点为A´和B´,则有AB=A´B´.
中小学数学中的很多图形都是轴对称图形,利用这些图形的对称轴性质,可以帮助我们解决一些计算和证明的几何问题.
旋转+截长补短:破解半角模型——口诀:
正方形,等直三,内含半角转一转.
共顶点,等线段,绕着顶点来旋转;
鸡爪图,三线段,抓住定角也旋转;
线段和,要得证,截长补短是正本;
1.如图,E是正方形ABCD的边DC上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线,并说明理由.
【分析】结论:AG平分∠BAF,AG平分∠BGF,GH平分∠EGM,CH平分∠DCM. (1)易证:△AFG≌△ABG,∴AG平分∠BAF,AG平分∠BGF;
(2)过点H作HN⊥BM,易证:△ABG≌△GNH,∴HN=BG,GN=AB,∴BG=CN,∴CN=HN,∴△CNH是等腰直角三角形,∴∠HCN=45°,∴CH平分∠DCN;(3)∵∠AGH=90°,AG平分∠BGE,∴可证GH平分∠EGM.
几何模型3.4 “半角”模型(旋转)(全等模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型3.4 “半角”模型(旋转)(全等模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共28页。PPT课件主要包含了模型特征,②大角的两边相等,解题思路,常见图形,BC+CD,2BC,线段之间的关系,①EFBE+FD,③BM·DGAB2,角度之间的关系等内容,欢迎下载使用。
几何模型3.3 “三叉口”模型(旋转)(全等模型)中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型3.3 “三叉口”模型(旋转)(全等模型)中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共17页。PPT课件主要包含了模型特征,②大角的两边相等,解题思路,常见图形,等边三角形,等腰直角三角形,正方形,解1连接PD,∴ADBP10,又∵AP8等内容,欢迎下载使用。
几何模型3.1 全等的四种模型(全等模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型3.1 全等的四种模型(全等模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共27页。PPT课件主要包含了平移模型,对称模型,三垂直型,旋转模型等内容,欢迎下载使用。












