2023年中考数学二轮复习必会几何模型剖析--3.5 “费马点”模型（旋转）（全等模型）（精品课件）

这是一份2023年中考数学二轮复习必会几何模型剖析--3.5 “费马点”模型（旋转）（全等模型）（精品课件），共10页。PPT课件主要包含了费马点性质，如何证明这个结论等内容，欢迎下载使用。
皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等. 据说费马在提出“费马大定理”时,在笔记本上写道：“我已经想到了一个绝妙的证明方法,但是这个地方不够写,我就不写了吧.”看得出那个时候纸确实挺贵的,几百年来,无数的数学家用一生的时间都没有证明出这条定理,直到1995年,才由英国数学家怀尔斯证明出来,此时费马已经逝世330年.
费马(1601-1665)向意大利物理学家托里拆利(1608-1647)提出了一个著名的极值问题,“求一点,使它到三角形三顶点的距离和最小”,并由托里拆利解决,“若三角形3个内角均小于120º,在三角形的三边各向其外侧作等边三角形,这三个等边三角形的外接圆交于一点T,该点T即称为托里拆利点,也称费马点.”而三个等边三角形的外接圆称为托里拆利圆.即该点所对三角形三边的张角相等,均为120º.所以三角形的费马点也称为三角形的等角中心.此后德国斯太纳((1796-1863)独立提出并推广了它,故又称斯太纳问题.
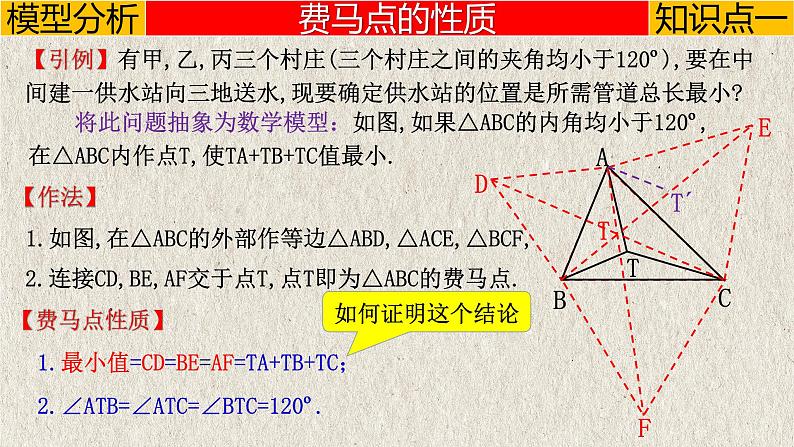
【引例】有甲,乙,丙三个村庄(三个村庄之间的夹角均小于120º),要在中间建一供水站向三地送水,现要确定供水站的位置是所需管道总长最小?
将此问题抽象为数学模型：如图,如果△ABC的内角均小于120º,在△ABC内作点T,使TA+TB+TC值最小.
【作法】 1.如图,在△ABC的外部作等边△ABD,△ACE,△BCF,
2.连接CD,BE,AF交于点T,点T即为△ABC的费马点.
2.∠ATB=∠ATC=∠BTC=120º.
1.最小值=CD=BE=AF=TA+TB+TC；
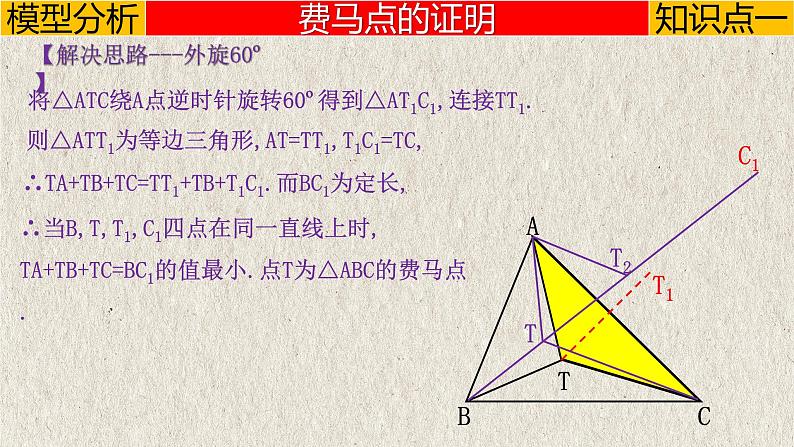
∴当B,T,T1,C1四点在同一直线上时,TA+TB+TC=BC1的值最小.点T为△ABC的费马点.
将△ATC绕A点逆时针旋转60º得到△AT1C1,连接TT1.
则△ATT1为等边三角形,AT=TT1,T1C1=TC,
∴TA+TB+TC=TT1+TB+T1C1.而BC1为定长,
【解决思路---外旋60º】
如图,等边△ABC和等边△CDE中B,C,D三点共线,AD,BE交于点P.点P为△ACE的费马点.
【例1】如图,在△ABC中,∠ACB=30º,BC=4,AC=3,在△ABC内部有点P,连接PA,PB,PC,求PA+PB+PC的最小值.