
2023年中考数学二轮复习必会几何模型剖析--5.3 K字型(一线三直角)模型(相似模型)(精品课件)
展开在坐标系中构造一线三直角
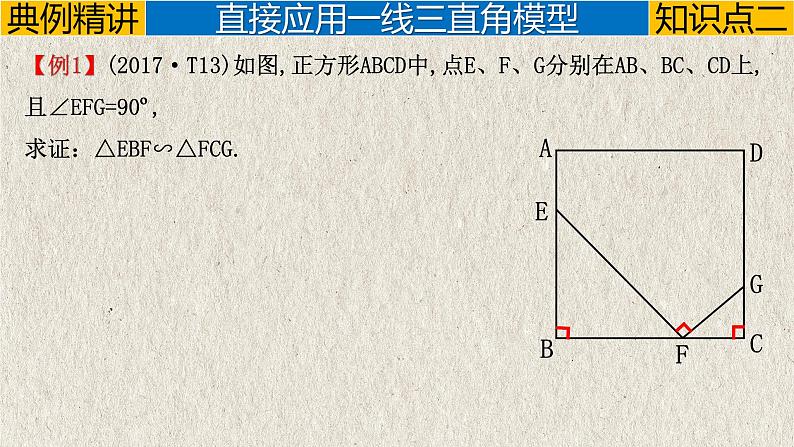
【例1】(2017·T13)如图,正方形ABCD中,点E、F、G分别在AB、BC、CD上,且∠EFG=90º,求证:△EBF∽△FCG.
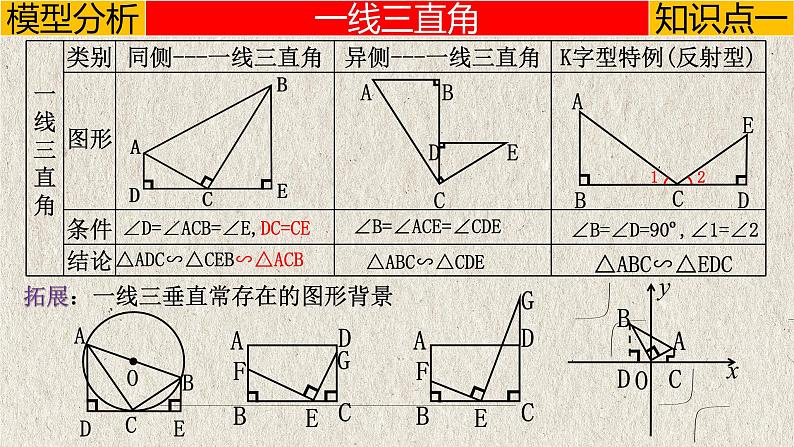
∠B=∠D=90º,∠1=∠2
∠D=∠ACB=∠E,DC=CE
△ADC∽△CEB∽△ACB
拓展:一线三垂直常存在的图形背景
∠B=∠ACE=∠CDE
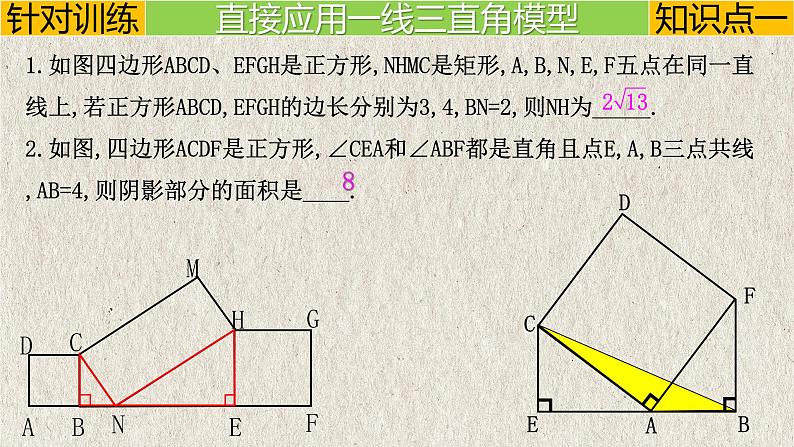
1.如图四边形ABCD、EFGH是正方形,NHMC是矩形,A,B,N,E,F五点在同一直线上,若正方形ABCD,EFGH的边长分别为3,4,BN=2,则NH为_____.2.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是____.
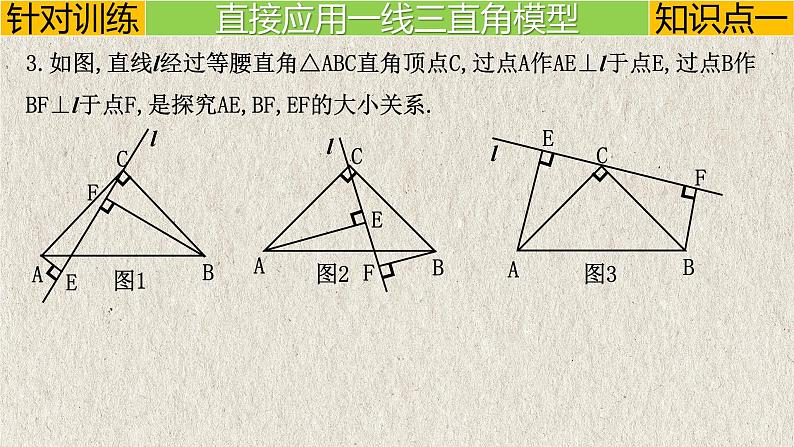
3.如图,直线l经过等腰直角△ABC直角顶点C,过点A作AE⊥l于点E,过点B作BF⊥l于点F,是探究AE,BF,EF的大小关系.
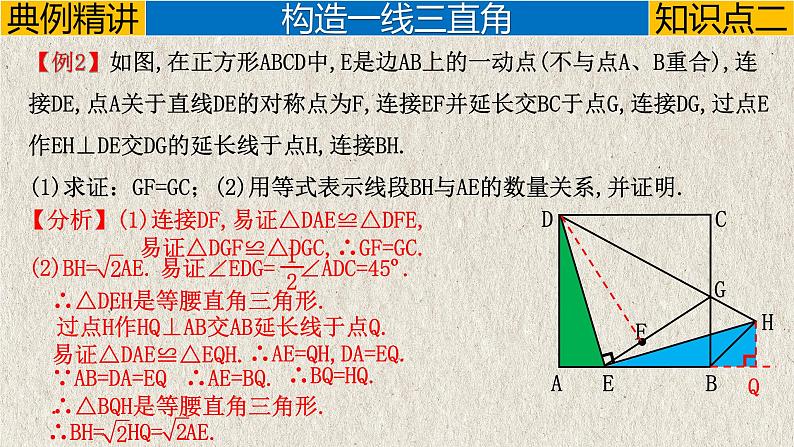
【例2】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH. (1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.
【分析】(1)连接DF,易证△DAE≌△DFE, 易证△DGF≌△DGC,∴GF=GC.
∴△DEH是等腰直角三角形.
过点H作HQ⊥AB交AB延长线于点Q.
易证△DAE≌△EQH.
∴AE=QH,DA=EQ.
∴△BQH是等腰直角三角形.
∠AEC=∠ACB=90º
【变形一】由(1),(3)→(2)如图,E是正方形ABCD的边AB上一点,∠CBH=45º,过点E作EH⊥DE交BH于点H,求证:∠EDH=45º.
在本题图中,除了正方形条件外,其实还存在另外三个条件与结论:(1)∠DEH=90º;(2)∠EDH=45º;(3)∠CBH=45º.其中任意两个组合均可得到第三个,本题是由(1),(2)结合得到(3).
【分析】可以采用构造三垂直思路,但是对于△DAE和△EQH,并没有已知的相等线段,此路不通.
不同的条件下方法可能会不同,利用好题目的已知条件,比如此处∠CBH=45º如何运用?
证明:在AD边上取点F使得AF=AE,连接EF.
∴∠DFE=135º=∠EBH,易证∠FDE=∠BEH,DF=EB,
∴△DFE≌△EBH,
∴△DEH是等腰直角三角形,
【变形二】由(2),(3)→(1)如图,E是正方形ABCD的边AB上一点, ∠EDH=∠CBH=45º,求证:DE⊥EH.
∴∠DEH=∠DBH=90º.
证明:∵∠EDH=45º,∠EBH=90º+45º=135º.
∴∠EDH+∠EBH=180º.
∴B、E、D、H四点共圆,连接BD.
1.在四边形ABCD中,∠BAD=∠ACB=90º,AB=AD,AC=4BC,若CD的长为5,则四边形ABCD的面积为____.
【例3】如图,将正方形OABC放在平面直角坐标系中,O是坐标原点,点A的坐标为(2,3),则点B的坐标为_______.
作x轴的垂线,构造一线三直角.
作y轴的垂线,构造一线三直角.
1.如图,在平面直角坐标系中,等腰直角三角形OAB的一个顶点在原点处,∠ABO=90º,OB=AB,已知点A(2,4),则点B的坐标为_______.2.如图,已知抛物线y=-0.5x2与直线AB交于A(-2,-4),B两点连接AO,BO,若∠AOB=90º,则点B的坐标为_______.
构造一线三直角的基本步骤
一线三直角是一个常见的相似模型,指的是有三个直角的顶点在同一条直线上构成的相似图形,也有称三垂直模型、K型图或M型图.(一线三等角不仅可以是直角,也可以是锐角或钝角)
(1)找图中已知的直角,顺着这个直角的顶点寻找或者构造模型中的一线;(2)构造其他直角,构造的直角的顶点必须在同一条直线上,这条直线可能在已知角的外部,也可能穿过这个角.
若出现一直角的顶点在一条直线上的形式,就可以构造两侧的直角三角形,利用全等三角形或相似三角形解决相关问题.本质就是找角、定线、构相似.
4.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90º而得,则AC所在直线的解析式是________.5.如图,点A(0,8),点B(4,0),连接AB,点M、N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__________________.
6.如图直角梯形ABCD中,AD//BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是____.7.如图,已知△ABC中∠ABC=90º,AB=BC,△ABC三个顶点在相互平行的三条直线上,且l1与l2之间的距离为2,l2与l3之间的距离为3,则AC的长是_____.
12.如图,在四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45º,则BD的长为______. 13.如图,已知∠ACB=90º,AD=BC,CD=BE,AE与BD相交于点F,则∠AFD=____.
4.如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=___.
【分析】动态问题先分析何时∠ABF最大.F点轨迹是以点A为圆心,AF为半径的圆,当BF与圆相切时,∠ABF最大,分别过点E、F作直线DA的垂线,垂足分别记为M、N,
易证△AME≌△FNA,
∴EM=AN=4×3/5=12/5.
∴S△ADE=1/2×5×12/5=6.
【分析】求三角形的面积,可以首先考虑面积公式,以BD为底,需作高 分别过C、E作BA的垂线,垂足分别记为点M、N.
故△BDE面积的最大值为8.
易证△DMC≌△END,
由tan∠ABC=1/2得:CM=4,BM=8,
设BD=x,则EN=DM=8-x.
∴S△BDE=1/2x(8-x)=-1/2x2+4x.
当x=4时,S△BDE取到最大值8.
6.如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接FG并延长,交4C的延长线于点P,若AB=5,CF=2,则线段EP的长是________.
【分析】有直角便可考虑构造三垂直.如下左图,过点E作EM⊥CD交CD于M点,过点G作GN⊥ME交ME延长线于点N,易证△FME≌△ENG,连接GA,点F作FH⊥AP交AP于H点,
易证△GAE∽△EHF,
∴△PHF∽△PAG.
∴FH:GA=PH:PA.
9.两块三角板如图放置,已知∠BAC=∠ADC=90º,∠ABC=45º,∠ACD=30º,BC= cm.(1)分别求线段AD,CD的长度;(2)求BD2的值。
(1)A(0,6),B(10,0)(2)
12.已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(12,0),点B(0,6),点P、Q分别为BC、AC边上的动点(P不与B、C重合),沿OP折叠该纸片,得点B´.沿PQ再次折叠纸片,使点C落在直线PB´上,得点C´.设BP=t,AQ=m.(1)试用含有t的式子表示m;(2)当点C´恰好落在边OA上时,求点P的坐标.
P1(2,6)或P2(6,6)
5.如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).(1)求证:△AEP≌△CEP;(2)判断CF与AB的位置关系,并说明理由;(3)求△AEF的周长.
解:(1)在△AEP和△CEP中.
∴△APE≌△CEP(SAS).
(2)∵△APE≌△CEP.
∴∠PAE=∠PCE.
∵∠EAP=∠BAP.
∴∠PCE=∠BAP.
∴∠PCE+∠CPA=∠BAP+∠AFC.
∴∠AFC=∠CPA=90º.
C△AEF=AE+AF+EF=CE+EF+AF=CF+AF.
(3)过点C作CH⊥BG交BG于点H, 过点P作PN⊥CF交CF于点N.
∴△AEF的周长为16.
易证△ABP≌△PHC.
∵NF=PB=CH=BF.
∴AF+FN=AF+FB=AB=8.
∴C△AEF=CF+AF=CN+NF+AF=PH+AB=2AB=16.
6.如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90º,FG⊥AD,垂足为点G.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.
解:(1)相等.过点F作FM⊥BA交BA 延长线于点M.
易证△EBC≌△FME.
∴BE=MF,BC=ME.
∴ME=AB,即BE=MA.
∴四边形AMFG是正方形.
(2)延长DH、FG交于点N.
易证△CDH≌△FNH.
∴CD=FN,FN=AD.
∴△DGN是等腰直角三角形,又H是DN中点.
7.如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90º,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长.
设BE=x,则MP=x,PN=3-x,EM=AB=3,CM=x-2.
解:①当∠PDC=90º时,如图2.
易证△ABE是等腰直角三角形,
②当∠DPC=90º时,如图3.
过点P作MN⊥BC于点M,与AD延长线交于点N.
易证△ABE≌△CMP,△CMP∽△PND.
解:(1)过点M分别作ME⊥AB于点E,MF⊥AC于点F.
易证△MEA≌△MFN.
几何模型6.4 “胡不归”模型(直角三角形模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型6.4 “胡不归”模型(直角三角形模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共26页。PPT课件主要包含了第四步计算,模型的特征,解题思想,折转直,解题步骤,12345模型等内容,欢迎下载使用。
几何模型5.5 “母子、旋转、三平行”模型(相似模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型5.5 “母子、旋转、三平行”模型(相似模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共22页。PPT课件主要包含了“母子”型相似,“旋转”型相似,三平行模型,④HC2HA·HB,②AC2AH·AB,∠ABD∠C,②AB2AD·AC,④△BAD∽△CAE,△ABC∽△ADE,②∠BAC∠DAE等内容,欢迎下载使用。
几何模型5.2 K字型(一线三等角)模型(相似模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型5.2 K字型(一线三等角)模型(相似模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共13页。PPT课件主要包含了∠B∠1∠D,△ABC∽△CDE,∠B∠1∠C,△FBD∽△DCE,∠1∠2∠ACE,∴△AOE∽△BFO,∵∠EOF45º,∴∠3∠1,∴AE•BF=4,∵AO=BO=2等内容,欢迎下载使用。












