2023年中考数学常见几何模型全归纳 专题06 相似模型-母子型（共角共边模型）和A（X）字型

中考经典几何模型与最值问题

每年中考高考，数学都是很受关注的一门学科。每次数学中考结束，相当一部分学生的心情都不轻松。如果有效刷题，有效学生，有一点很重要，那就是搜集经典题目，汇总经典题型，尤其是对一些经典的数学模型，多解题或者易错题，不妨专门用一个本子搜集一下，整理一下，考前复习一下，效果会很不错。

今天整理了初三中考总复习阶段在教学过程中收集的经典题目，一共有16讲，包括原卷版和解析版，供大家学习复习参考。

经典题目1：这是一道非常经典的最值问题，最值模型将军饮马和一箭穿心。对于利用一穿心求圆外一点到圆上的最大值和最小值问题，弄懂这道题就够了。

经典题目2：上面三道题是费马点经典问题，旋转转化是费马点问题的关键，其核心思想是化折为直，掌握关键技巧，掌握核心思想，才能解决一类数学题目。

经典题目3：阿氏圆经典题目，这道题目实际包括了隐圆模型，一箭穿心模型等常见几何模型，核心思想依旧是化值为直，构造子母相似三角形实现线段的转化。

经典题目4：这是中考出现频率比较高的胡不归问题，也是经典最值问题，这是一个有历史故事的最值问题。构造锐角三角函数实现线段的转化，利用垂线段最短解决问题。

专题06 相似模型-母子型（共角共边模型）和A（X）字型

相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到相似三角形的问题就信心更足了．本专题重点讲解相似三角形的母子模型与A（X）字模型．

模型1.“母子”模型(共边角模型)

【模型解读与图示】“母子”模型的图形（通常有一个公共顶点和另外一个不是公共的顶点，由于小三角形寓于大三角形中，恰似子依母怀），也是有一个“公共角”，再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似．“双垂线”型是其特例。

 “ 母子”模型（斜射影）           双垂直（射影定理）        “母子型”的变形

斜射影结论：

△ABD∽△ACB，AB2＝AD·AC.

双垂直结论：

①△ABD∽△ACB，AB2＝AD·AC；②△ADC∽△ACB，AC2＝AD·AB；③△CDB∽△ACB，CB2＝BD·BA.

1．（2022·贵州贵阳·中考真题）如图，在中，是边上的点，，，则与的周长比是（       ）

A． B． C． D．

2．（2022·陕西汉中·九年级期末）如图，是等腰直角斜边的中线，以点为顶点的绕点旋转，角的两边分别与、的延长线相交，交点分别为点、，与交于点，与交于点，且．(1)如图1，若，求证：；(2)如图2，若，求证：；

(3)如图2，过作于点，若，，求的长．

3．（2022·浙江绍兴·九年级期末）如果两个相似三角形的对应边存在2倍关系，则称这两个相似三角形互为母子三角形．（1）如果与互为母子三角形，则的值可能为（    ）

A．2    B．    C．2或

（2）已知：如图1，中，是的角平分线，．

求证：与互为母子三角形．

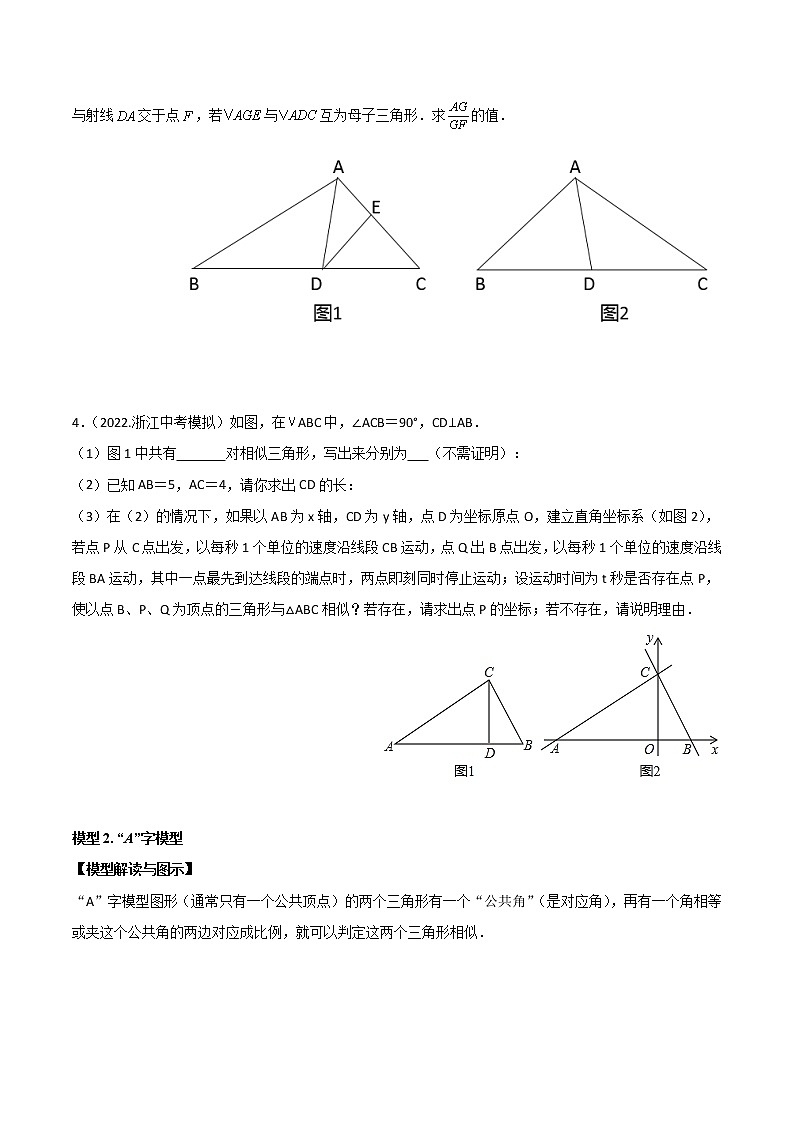
（3）如图2，中，是中线，过射线上点作，交射线于点，连结，射线与射线交于点，若与互为母子三角形．求的值．

4．（2022.浙江中考模拟）如图，在ABC中，∠ACB＝90°，CD⊥AB．

（1）图1中共有　   　对相似三角形，写出来分别为　 （不需证明）：

（2）已知AB＝5，AC＝4，请你求出CD的长：

（3）在（2）的情况下，如果以AB为x轴，CD为y轴，点D为坐标原点O，建立直角坐标系（如图2），若点P从C点出发，以每秒1个单位的速度沿线段CB运动，点Q出B点出发，以每秒1个单位的速度沿线段BA运动，其中一点最先到达线段的端点时，两点即刻同时停止运动；设运动时间为t秒是否存在点P，使以点B、P、Q为顶点的三角形与△ABC相似？若存在，请求出点P的坐标；若不存在，请说明理由．

模型2. “A”字模型

【模型解读与图示】

“A”字模型图形（通常只有一个公共顶点）的两个三角形有一个“公共角”（是对应角），再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．

1．（2022·湖南怀化·中考真题）如图，△ABC中，点D、E分别是AB、AC的中点，若S△ADE＝2，则S△ABC＝_____．

2．（2022·浙江杭州·中考真题）如图，在ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，EF，已知四边形BFED是平行四边形，．(1)若，求线段AD的长．(2)若的面积为1，求平行四边形BFED的面积．

3．（2022·浙江宁波·中考真题）(1)如图1，在中，D，E，F分别为上的点，交于点G，求证：．

(2)如图2，在（1）的条件下，连接．若，求的值．

(3)如图3，在中，与交于点O，E为上一点，交于点G，交于点F．若平分，求的长．

4．（2022·辽宁·中考真题）如图，在中，，D，E，F分别为的中点，连接．(1)如图1，求证：；(2)如图2，将绕点D顺时针旋转一定角度，得到，当射线交于点G，射线交于点N时，连接并延长交射线于点M，判断与的数量关系，并说明理由；(3)如图3，在（2）的条件下，当时，求的长．

模型3. “X”字模型（“8”模型）

【模型解读与图示】

“X”字模型图形的两个三角形有“对顶角”，再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似．

1．（2022·河北·中考真题）如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A，B的连线与钉点C，D的连线交于点E，则

（1）AB与CD是否垂直？______（填“是”或“否”）；（2）AE＝______．

2．（2022·四川内江·中考真题）如图，在矩形ABCD中，AB＝6，BC＝4，点M、N分别在AB、AD上，且MN⊥MC，点E为CD的中点，连接BE交MC于点F．

(1)当F为BE的中点时，求证：AM＝CE；(2)若＝2，求的值；(3)若MN∥BE，求的值．

3．（2022·广西贵港·中考真题）已知：点C，D均在直线l的上方，与都是直线l的垂线段，且在的右侧，，与相交于点O．

(1)如图1，若连接，则的形状为______，的值为______；

(2)若将沿直线l平移，并以为一边在直线l的上方作等边．

①如图2，当与重合时，连接，若，求的长；

②如图3，当时，连接并延长交直线l于点F，连接．求证：．

4．（2022·江苏镇江·九年级期末）梅涅劳斯（Menelaus）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图（1），如果一条直线与△ABC的三边AB，BC，CA或它们的延长线交于F、D、E三点，那么一定有．

下面是利用相似三角形的有关知识证明该定理的部分过程：

证明：如图（2），过点A作，交DF的延长线于点G，

则有，，∴．

请用上述定理的证明方法解决以下问题：

(1)如图（3），△ABC三边CB，AB，AC的延长线分别交直线l于X，Y，Z三点，证明：．

(2)如图（4），等边△ABC的边长为2，点D为BC的中点，点F在AB上，且，CF与AD交于点E，则AE的长为________．

(3)如图（5），△ABC的面积为2，F为AB中点，延长BC至D，使，连接FD交AC于E，则四边形BCEF的面积为________．

课后专项训练：

1．（2022•江苏中考模拟）对于两个相似三角形，如果沿周界按对应点顺序环绕的方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．例如，如图（1），△CDE∽△CAB，且沿周界CDEC与CABC环绕的方向（同为逆时针方向）相同，因此△CDE和△CAB互为顺相似；如图（2），△CDE∽△CBA，且沿周界CDEC与CBAC环绕的方向相反，因此△CDE和△CBA互为逆相似．

（1）根据以上材料填空：

①如图（3），AB∥CD，则△AOB∽△COD，它们互为　   　相似（填“顺”或“逆”，下同）；

②如图（4），Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，则△ABC∽　   　，它们互为　   　相似；

③如图（5），若∠DAB＝∠EBC＝90°，并且BD⊥CE于点F，则△ABD∽　   　，它们互为　   　相似；

（2）如图（6），若△AOB∽△COD，指出图中另外的一对相似三角形并说明理由，同时指出它们互为顺相似还是互为逆相似；

（3）如图（7），在Rt△ABC中，∠C＝90°，AC＝20，BC＝15，点P在△ABC的斜边上，且AP＝16，过点P画直线截△ABC，使截得的一个三角形与△ABC相似，则满足的截线共有　   　条．

2．（2022·吉林·中考真题）下面是王倩同学的作业及自主探究笔记，请认真阅读并补充完整．

【作业】如图①，直线，与的面积相等吗？为什么？

解：相等．理由如下：设与之间的距离为，则，．∴．

【探究】(1)如图②，当点在，之间时，设点，到直线的距离分别为，，则．

证明：∵                   

(2)如图③，当点在，之间时，连接并延长交于点，则．

证明：过点作，垂足为，过点作，垂足为，则，

∴          ．

∴          ．

∴．

由【探究】（1）可知          ，∴．

(3)如图④，当点在下方时，连接交于点．若点，，所对应的刻度值分别为5，1.5，0，的值为          ．

3．（2022·上海·九年级专题练习）如图，在中，，，，平分，交边于点，过点作的平行线，交边于点．

（1）求线段的长；（2）取线段的中点，联结，交线段于点，延长线段交边于点，求的值．

4．（2022·上海市奉贤区古华中学九年级期中）已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE＝AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．

（1）求证：△BND∽△CNM；（2）如果AD2＝AB•AF，求证：CM•AB＝DM•CN．

5．（2022•安庆模拟）在四边形ABCD中，对角线AC、BD相交于点O．

（1）如图①，若四边形ABCD为矩形，过点O作OE⊥BC，求证：OE＝CD．

（2）如图②，若AB∥CD，过点O作EF∥AB分别交BC、AD于点E、F．求证：＝2．

（3）如图③，若OC平分∠AOB，D、E分别为OA、OB上的点，DE交OC于点M，作MN∥OB交OA于一点N，若OD＝8，OE＝6，直接写出线段MN长度．

6．（2022•重庆中考模拟）问题提出：如图1，D、E分别在△ABC的边AB、AC上，连接DE，已知线段AD＝a，DB＝b，AE＝c，EC＝d，则S△ADE，S△ABC和a，b，c，d之间会有怎样的数量关系呢？

问题解决：探究一：（1）看到这个问题后，我们可以考虑先从特例入手，找出其中的规律．如图2，若DE∥BC，则∠ADE＝∠B，且∠A＝∠A，所以△ADE∽△ABC，可得比例式：而根据相似三角形面积之比等于相似比的平方．可得．根据上述这两个式子，可以推出：．

（2）如图3，若∠ADE＝∠C，上述结论还成立吗？若成立，请写出证明过程；着不成立，请说明理由．

探究二：回到最初的问题，若图1中没有相似的条件，是否仍存在结论：？方法回顾：两个三角形面积之比，不仅可以在相似的条件下求得，当两个三角形的底成高具有一定的关系时，也可以解决．如图4，D在△ABC的边上，做AH⊥BC于H，可得：．借用这个结论，请你解决最初的问题．

延伸探究：（1）如图5，D、E分别在△ABC的边AB、AC反向延长线上，连接DE，已知线段AD＝a，AB＝b，AE＝c，AC＝d，则　 　．（2）如图6，E在△ABC的边AC上，D在AB反向延长线上，连接DE，已知线段AD＝a，AB＝b，AE＝c，AC＝d，　 　．

结论应用：如图7，在平行四边形ABCD中，G是BC边上的中点，延长GA到E，连接DE交BA的延长线于F，若AB＝5，AG＝4，AE＝2，▱ABCD的面积为30，则△AEF的面积是 　 　．

7．（2022·贵州铜仁·中考真题）如图，在四边形中，对角线与相交于点O，记的面积为，的面积为．（1）问题解决：如图①，若AB//CD，求证：

（2）探索推广：如图②，若与不平行，（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由．（3）拓展应用：如图③，在上取一点E，使，过点E作交于点F，点H为的中点，交于点G，且，若，求值．

8．（2022·湖北随州·九年级期末）请阅读下列材料，并完成相应的任务．

梅涅劳斯（Menelaus）是公元一世纪时的希腊数学家兼天文学家，著有几何学和三角学方面的许多书籍．梅涅劳斯发现，三角形各边（或其延长线）被一条不过任何一个顶点也不与任何一条边平行的直线所截，这条直线可能与三角形的两条边相交（一定还会与一条边的延长线相交），也可能与三条边都不相交（与三条边的延长线都相交）．他进行了深入研究并证明了著名的梅涅劳斯定理（简称梅氏定理）：

设D，E，F依次是△ABC的三边AB，BC，CA或其延长线上的点，且这三点共线，则满足．

这个定理的证明步骤如下：

情况①：如图1，直线DE交△ABC的边AB于点D，交边AC于点F，交边BC的延长线与点E．

过点C作CM∥DE交AB于点M，则，（依据），

∴＝，

∴BE•AD•FC＝BD•AF•EC，即．

情况②：如图2，直线DE分别交△ABC的边BA，BC，CA的延长线于点D，E，F．

…

（1）情况①中的依据指：　                             　；

（2）请你根据情况①的证明思路完成情况②的证明；

（3）如图3，D，F分别是△ABC的边AB，AC上的点，且AD:DB＝CF:FA＝2:3，连接DF并延长，交BC的延长线于点E，那么BE:CE＝　   　．

9.（2022长宁一模）已知, 在 中, , 点 是射线 上的动点, 点 是边 上的动点，且 , 射线 交射线 于点 ．

（1）如图 1, 如果 , 求 的值；

（2）联结, 如果 是以为腰的等腰三角形，求线段的长；

（3）当点在边上时, 联结, 求线段的长．

10.（2022松江中考模拟）如图，已知在△ABC中，BC＞AB，BD平分∠ABC，交边AC于点D，E是BC边上一点，且BE＝BA，过点A作AG∥DE，分别交BD、BC于点F、G，联结FE．（1）求证：四边形AFED是菱形；（2）求证：AB2＝BG•BC；（3）若AB＝AC，BG＝CE，联结AE，求的值．

11．（2022•静安区期末）如图1，四边形ABCD中，∠BAD的平分线AE交边BC于点E，已知AB＝9，AE＝6，AE2＝AB•AD，且DC∥AE．（1）求证：DE2＝AE•DC；（2）如果BE＝9，求四边形ABCD的面积；

（3）如图2，延长AD、BC交于点F，设BE＝x，EF＝y，求y关于x的函数解析式，并写出定义域．

12．（2022·浙江·九年级单元测试）如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，且＝．

（1）求证 △ACD∽△ABC；（2）若AD＝3，BD＝2，求CD的长．

13．（2021·广西百色·中考真题）如图，△ABC中，AB＝AC，∠B＝72°，∠ACB的平分线CD交AB于点D，则点D是线段AB的黄金分割点．若AC＝2，则BD＝______．

14．（2022·江苏盐城·中考真题）如图，在与中，点、分别在边、上，且，若___________，则．请从①；②；③这三个选项中选择一个作为条件（写序号），并加以证明．