2023年四川省自贡市初中数学模拟试卷（一）（含答案）

这是一份2023年四川省自贡市初中数学模拟试卷（一）（含答案），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
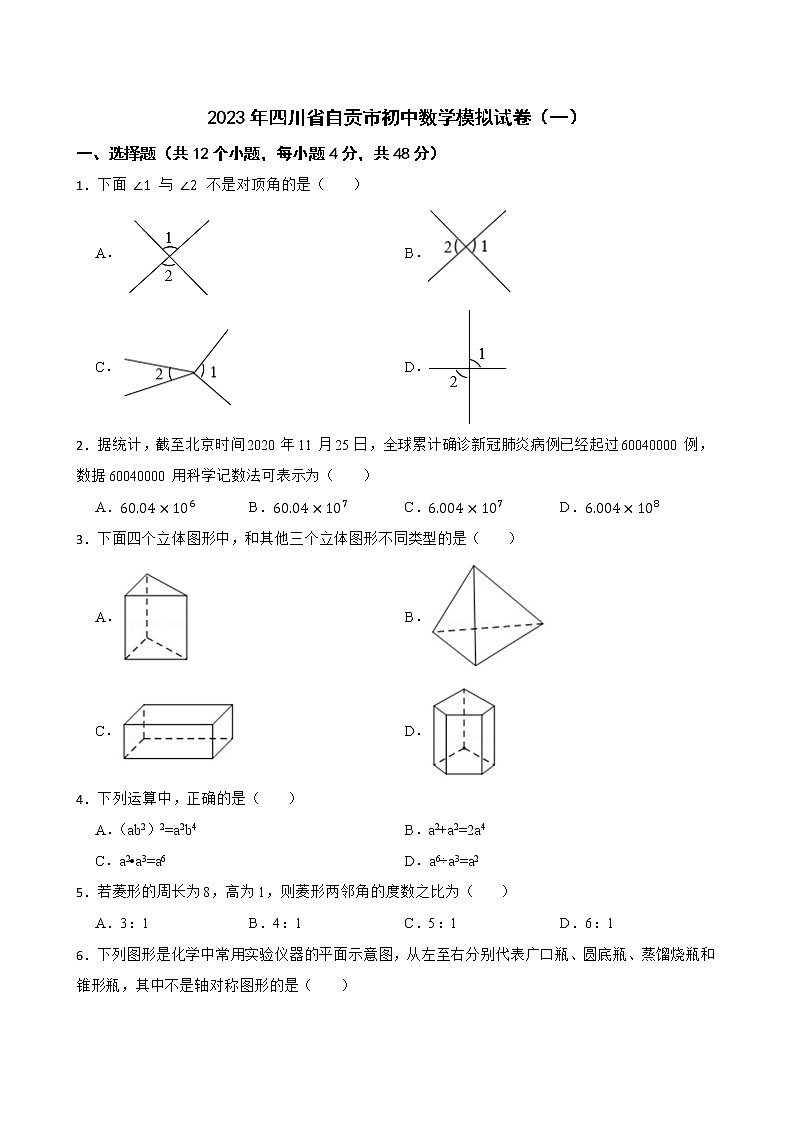
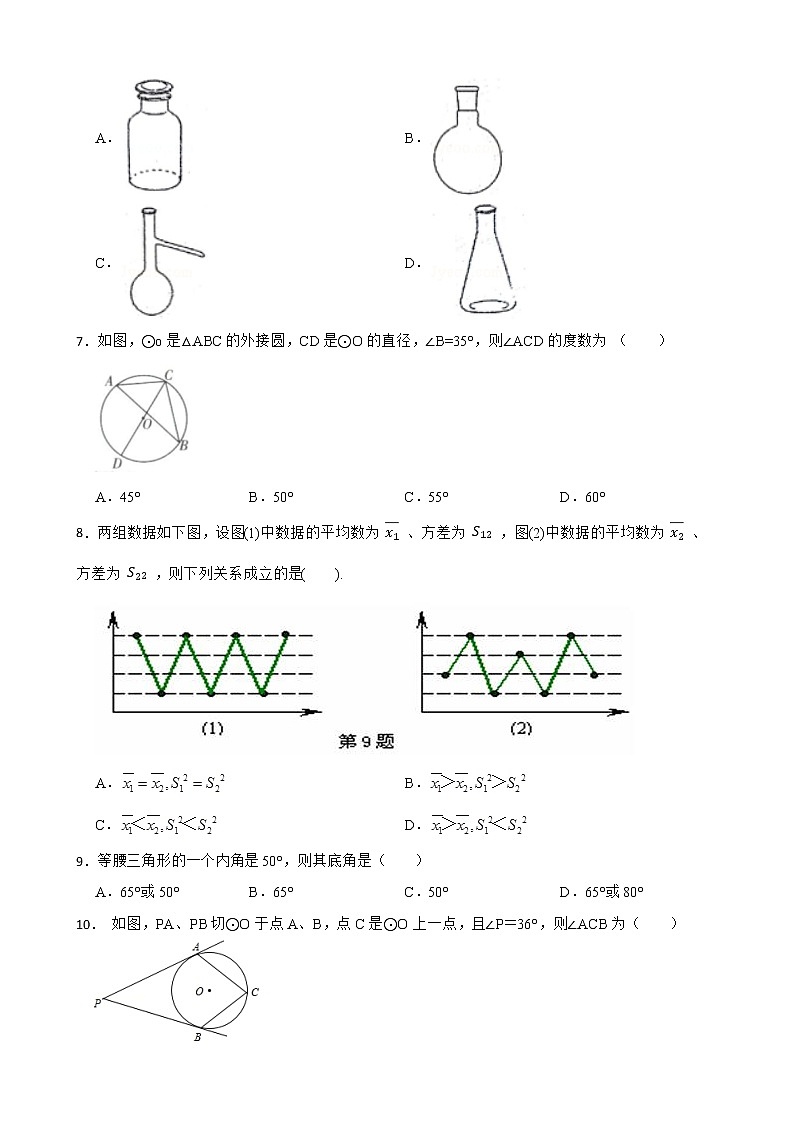
 2023年四川省自贡市初中数学模拟试卷（一）一、选择题（共12个小题，每小题4分，共48分）1．下面 与 不是对顶角的是（　　）  A． B．C． D．2．据统计，截至北京时间2020年11月25日，全球累计确诊新冠肺炎病例已经起过60040000例，数据60040000用科学记数法可表示为（　　）  A． B． C． D．3．下面四个立体图形中，和其他三个立体图形不同类型的是（　　）A． B．C． D．4．下列运算中，正确的是（　　）   A．（ab2）2=a2b4 B．a2+a2=2a4C．a2•a3=a6 D．a6÷a3=a25．若菱形的周长为8，高为1，则菱形两邻角的度数之比为（　　）   A．3：1 B．4：1 C．5：1 D．6：16．下列图形是化学中常用实验仪器的平面示意图，从左至右分别代表广口瓶、圆底瓶、蒸馏烧瓶和锥形瓶，其中不是轴对称图形的是（　　）   A． B．C． D．7．如图，⊙o是△ABC的外接圆，CD是⊙O的直径，∠B=35°，则∠ACD的度数为 （　　）A．45° B．50° C．55° D．60°8．两组数据如下图，设图(1)中数据的平均数为 、方差为 ，图(2)中数据的平均数为 、方差为 ，则下列关系成立的是(　　).   A． B．C． D．9．等腰三角形的一个内角是50°，则其底角是（　　）A．65°或50° B．65° C．50° D．65°或80°10． 如图，PA、PB切⊙O于点A、B，点C是⊙O上一点，且∠P＝36°，则∠ACB为（　　）A．54° B．72° C．108° D．144°11．如图，在Rt△ABC中，∠C＝90°，AC＝9，BC＝12，则点C到AB的距离是（　　）  A． B． C． D．12．二次函数y＝ax2+bx+c（a≠0）的图象与x轴的两个交点横坐标为﹣2，x0，且满足（a+b+c）（4a+2b+c）＜0，与y轴的负半轴相交，抛物线经过点A（﹣1，y1），B（﹣ ，y2），C（1，y3），正确结论是（　　）  A．y3＞y2＞y1 B．y3＞y1＞y2 C．y1＞y2＞y3 D．y1＞y3＞y2二、填空题（共6个小题，每小题4分，共24分）13．绝对值小于4的所有负整数的和是　     　．14．多项式 的公因式是　     　.   15．若（）•ω=1，则ω=　     　 ．16．如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生700人，则据此估计步行的有　     　人．  17．如图，点 是等边 内的一点， ， ， .若点 是 外的一点，且 ，则 的度数为　     　．  18．如图，在菱形ABCD中，AB=6，∠B=60°，点E在边AD上，且AE=2。若直线l经过点E，将该菱形的面积平分，并与菱形的另一边交于点F，则线段EF的长为　     　。三、解答题（共8个题，共78分）19．解不等式组： 并把解集在数轴上表示出来．  20．如图，在△ABC与△DEF中，如果AB=DE，BE=CF，∠ABC=∠DEF；求证：AC∥DF．21．为了防止雾霾，某口罩生产企业需要在若干天内加工2400个口罩，在实际生产中，由于提高了生产技术水平，每天加工的个数为原来的1.5倍，从而提前2天完成任务，问该企业原计划每天生产多少个口罩？   22．2021年，“碳中和、碳达峰”成为高频热词．为了解学生对“碳中和、碳达峰”知识的知晓情况，某校团委随机对该校九年级部分学生进行了问卷调查，调查结果共分成四个类别：A表示“从未听说过”，B表示“不太了解”，C表示“比较了解”，D表示“非常了解”．根据调查统计结果，绘制成两种不完整的统计图．请结合统计图，回答下列问题．（1）参加这次调查的学生总人数为　     　人；（2）扇形统计图中，B部分扇形所对应的圆心角是　     　；（3）将条形统计图补充完整；（4）在D类的学生中，有2名男生和2名女生，现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员，请利用画树状图或列表的方法，求所抽取的2名学生恰好是1名男生和1名女生的概率．23．已知双曲线与直线相交于A（-3，m）、B两点.（1）直接写出此双曲线的解析式；（2）若点M（a，b），且a，b都是不大于3的正整数，用画树状图法或列表法求点M在双曲线上的概率.24．如图，在等腰中，，以为直径作，交于点D，过点D作，垂足为E．（1）求证：是的切线；（2）如果，，求的长．25．为加强对市内道路交通安全的监督，王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB（如图所示），当无人机在限速道路的正上方C处时，测得限速道路的起点A的俯角是37°，无人机继续向右水平飞行220米到达D处，此时又测得起点A的俯角是30°，同时测得限速道路终点B的俯角是45°（注：即四边形ABDC是梯形）.（1）求限速道路AB的长（精确到1米）；（2）如果李师傅在道路AB上行驶的时间是1分20秒，请判断他是否超速？并说明理由.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，）26．综合与探究如图，已知抛物线经过，两点，交y轴于点C．（1）求抛物线的解析式，连接，并求出直线的解析式；（2）请在抛物线的对称轴上找一点P，使的值最小，此时点P的坐标是　          　（3）点Q在第一象限的抛物线上，连接CQ，BQ，求出△BCQ面积的最大值．（4）点M为x轴上一动点，在抛物线上是否存在一点N，使得以A、C、M、N四点为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．
答案解析部分1．【答案】C2．【答案】C3．【答案】B4．【答案】A5．【答案】C6．【答案】C7．【答案】C8．【答案】B9．【答案】A10．【答案】B11．【答案】A12．【答案】B13．【答案】-614．【答案】4ab15．【答案】﹣a﹣216．【答案】28017．【答案】150°18．【答案】19．【答案】解：解x﹣2＞0得：x＞2；  解不等式2（x+1）≥3x﹣1得：x≤3．∴不等式组的解集是：2＜x≤3．20．【答案】证明：∵BE=CF，∴BE+EC=CF+EC，即BC=EF，在和中，，∴，∴，∴AC∥DF.21．【答案】解：设该企业原计划每天生产x个口罩，依题意得：  解之得：x=400.答：该企业原计划每天生产400个口罩.22．【答案】（1）40（2）108°（3）解：C类别人数为（人），补全图形如下：（4）解：画树状图为：共有12种等可能的结果数，其中恰好选中1名男生和1名女生的结果数为8，∴所抽取的2名学生恰好是1名男生和1名女生的概率．23．【答案】（1）解：；（2）解：列表如下： （a， b）1231（1，1）（1，2）（1，3）2（2，1）（2，2）（2，3）3（3，1）（3，2）（3，3）由上表可知，一共有9种等可能结果，其中在双曲线上的有2种，所以点M在双曲线上的概率为.24．【答案】（1）证明：连接，∵，∴，∵等腰中，，∴，∵∴，∴，∴，∴，∴，∵是的半径，∴是的切线；（2）解：∵，∴，∴，∴，∵为的中点，∴，∵，∴，连接，∵为的直径，∴，∵，∴，∴，∴，即的长为．25．【答案】（1）解：根据题意，得∠CAB=37°，CD=220米，∠DAB=30°，∠DBA=45°， 如图，过点C和点D作CE和DF垂直于AB于点E和F，∵CD∥AB，∴四边形CDFE是矩形，∴CE=DF，CD=EF，∵∠DBA=45°，∴DF=BF，设DF=BF=CE=x米，在Rt△ADF中，∠DAF=30°，DF=x米，∴AF=DF÷tan30°=DF=x（米），∴AE=AF-EF=（x-220）米，在Rt△AEC中，∠CAE=37°，∵CE=AE•tan37°，∴x=（x-220）×0.75，解得x=60（3+4）=（180+240）米，∴AE=x-220=（320+240）米，FB=x=（180+240）（米），∴AB=AE+EF+FB=320+240+220+180+240=780+420≈1507（米），答：限速道路AB的长约为1507米；（2）解：∵1分20秒=小时， ∴该汽车的速度约为：1507÷≈67.8km/h＞60km/h，∴该车超速.26．【答案】（1）解：∵抛物线经过，两点，∴，解得：，∴抛物线的解析式为；∵抛物线与y轴的交点为C，∴，设直线的解析式为，把点B、C的坐标代入得：，解得：，∴直线的解析式为；（2）（3）解：过Q作QD⊥x轴，交BC于D，设Q，其中 ，则D，∴，∵，∴，∴，当时，取最大值，最大值为8，∴△BCQ的最大面积为8；（4）解：存在，理由如下：由题意可设点，，当以A、C、M、N四点为顶点的四边形是平行四边形，则可分：①当AC为对角线时，连接MN，交AC于点D，如图所示：∵四边形ANCM是平行四边形，∴点D为AC、MN的中点，∴根据中点坐标公式可得：，即，解得：，∴；②当AM为对角线时，同理可得：，即，解得：，∴；③当AN为对角线时，同理可得：，即，解得：，∴；∴综上所述：当A、C、M、N四点为顶点的四边形是平行四边形，点N的坐标为或或．