鲁教版 (五四制)九年级上册6 二次函数的应用试讲课ppt课件

这是一份鲁教版 (五四制)九年级上册6 二次函数的应用试讲课ppt课件，文件包含鲁教版五四制数学九上《二次函数的应用3》课件pptx、鲁教版五四制数学九上《二次函数的应用3》教案doc等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。
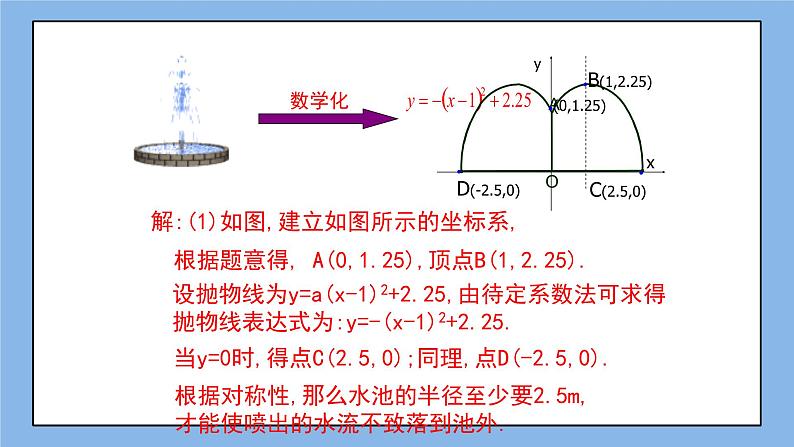
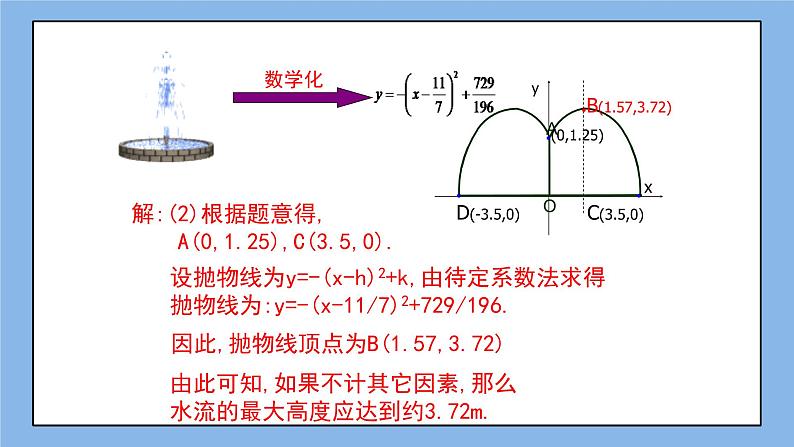
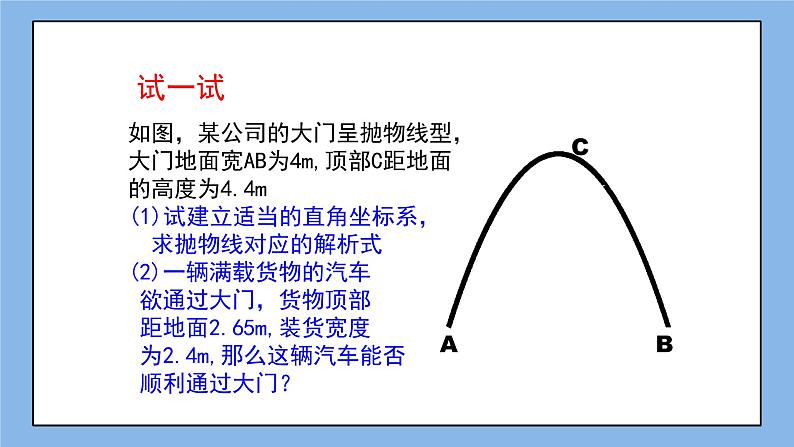
§3.6  二次函数的应用（3）【学习目标】1、会建立适当的直角坐标系，能准确求出二次函数的解析式。2、能够分析和表示实际问题中变量之间的二次函数关系。3、经历探索实际问题的过程，感受数学模型思想和数学的应用价值。【学习重点】分析和表示变量之间的二次函数关系，求函数解析式。【学习难点】探索实际问题，构建函数模型。【学习流程】一、自主预习例题：某公司的大门呈抛物线型，大门地面宽AB为4m，顶点C距地面的高度为4.4m，（1）试建立适当的直角坐标系，求抛物线的解析式；（2）一辆满载货物的汽车欲通过大门，货物顶部距地面2.65米，装货宽度为2.4m，那么这辆汽车能否顺利通过大门？【预习导航】请自学例题，在10分钟内，完成下列预习问题：（1）请建立适当的平面直角坐标系。（2）在该坐标系中，点A、B、C的坐标依次是_______、_______、_______；（3）根据函数图象，我们设出二次函数的解析式是_________________；（4）根据三个点的坐标，请求出抛物线的解析式。【问题解答】解：    【学习疑惑】通过预习，我的（发现/疑惑）是__________________________________；二、合作交流【疑惑交流】1、点评：预习导学中存在问题。2、思考：在坐标系中，如何来判断“车辆能否顺利通过大门”？3、交流：结合坐标轴，讨论解题方法的灵活性。4、讨论：请独立思考后，总结此类问题的一般解法是什么？请用①②③……来表述。【知识研讨】请根据所提供的坐标系，完成变式练习：变式1：在该情景中，如果装货宽度为2.4米的汽车能够顺利通过大门，那么货物顶部距地面的最大高度是多少？（精确到0.01m）     变式2：在该情景中，若该门口的路面改为双车道，货车是否可以顺利通过呢？     变式3：改为双车道后，为了安全起见，在正中间设有宽为0.4m的隔离带，此时，车辆还能顺利通过吗？      【合作交流】1、结合三个变式，进一步体会“用二次函数模型解实际问题”的思路。2、对于此类问题，你还有什么疑惑吗？若有，请说明。三、达标测评【知识巩固】1、  喷泉问题某公园要建造一圆形喷水池，水流在各方向沿形状相同的抛物线落下，如果喷头所在处A（0，1.25），水流路线最高处B（1，2.25），则该抛物线的解析式为___________；如果不考虑其他因素，那么水池的半径至少要______ 米，才能使喷出的水流不致落到池外。     2、  拱桥问题河北赵县的赵州桥是我国著名的石拱桥。它的桥拱是抛物线型，建立如图所示的坐标系，其表达式是，当水位线在AB的位置时，水面的宽度为30m，这时水面离桥顶的高度h是（    ）米。A、5米      B、6米；   C、8米；     D、9米 3、投篮问题：姚明在某次比赛中, 出手投篮，球的运动路线是抛物线            的一部分,若命中篮圈中心,则他与篮底的距离L是（     ）A、3.5cm   B、4m   C、4.5cm     D、4.6cm4、隧道问题：某隧道的截面由抛物线和矩形构成，矩形的长=，宽=，如图，建立平面直角坐标系，顶点到坐标原点的距离为．（1）求抛物线的解析式；（2）一辆货运卡车高，宽2.4m，它能通过该隧道吗？（3）如果该隧道内设双行道，在隧道正中间设有0.4m的隔离带，则：该辆货运卡车还能通过隧道吗？        四、课堂小结：1、本节课我们接触了几种实际生活情境？问题的处理方式相同吗？2、利用二次函数模型解决问题时，最需要注意的是什么？3、通过“实际问题数学化”的探究，你最深的感受是什么？4、对于本节课，你还有哪些疑惑和困难？五、作业设置（一）巩固作业：课后习题3.14第1、2题六、课后反思： 收获疑惑知识  方法