







高中数学5.2 余弦函数的图象与性质再认识优秀课件ppt
展开课时把关练
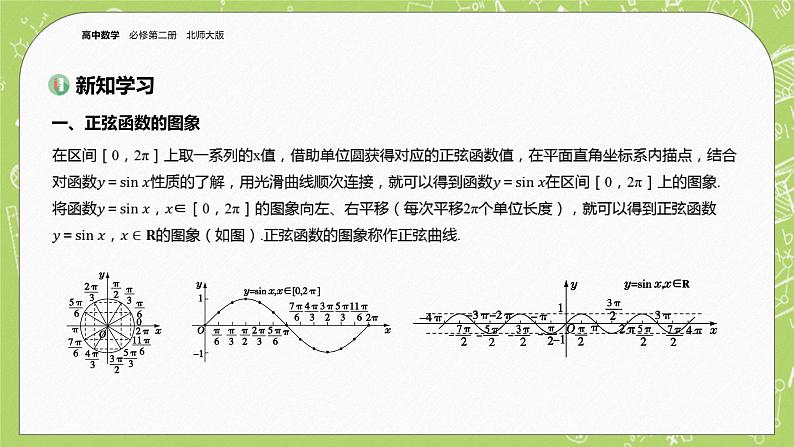
§5 正弦函数、余弦函数的图象与性质再认识
5.1 正弦函数的图象与性质再认识
1.函数y=1-sin x,x∈[0,2π]的大致图象是( )
A B C D
2.M和m分别是函数y=sin x-1的最大值和最小值,则M+m等于( )
A. B.- C.- D.-2
3.下列关系式中正确的是( )
A.sin 11°<cos 10°<sin 168° B.sin 168°<sin 11°<cos 10°
C.sin 11°<sin 168°<cos 10° D.sin 168°<cos 10°<sin 11°
4.函数y=-sin 2x,x∈R是( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为2π的奇函数 D.最小正周期为2π的偶函数
5.已知函数f(x)=,则f(x)的最大值为( )
A.-2 B.-1 C.0 D.1
6.已知α,β∈,且cos α+ sin β>0,则下列式子正确的是( )
A.α+β<π B.α+β>π C.α+β=π D.α+β<π
7.已知函数f(x)=sin x- ,现有命题:① f(x)的最大值为0;② f(x)是偶函数;③ f(x)的周期为π;④ f(x)的图象关于直线x=对称.其中真命题的个数是( )
A.4 B.3 C.2 D.1
8.若方程sin2x-2sin x-a=0在x∈R上有解,则a的取值范围是( )
A.[-1,+∞) B.(-1,+∞) C.[-1,3] D.[-1,3)
9.(多选题)下列说法正确的是( )
A.y=|sin x|的定义域为R B.y=3sin x+1的最小值为1
C.y=-sin x为奇函数 D.y=sin x-1的单调递增区间为 (k∈Z)
10.(多选题)已知函数y=2sin x的定义域为[a,b],值域为[-2,1],则b-a可能的取值是( )
A. B. C. D.
11. 函数y=+的定义域是 .
12.下列结论中正确的有 .(只写出正确结论的序号即可)
① 若函数f(x)的定义域为[1,2],则函数f(2cos x)的定义域为,k∈Z;
② 若函数y=lg(ax2 +2x+a)的值域为R,则实数a的取值范围为(0,1];
③ 函数f(x)=的最大值为6;④ 函数y=sin2x-sin x+的值域为.
13.写出一个最小正周期为2的奇函数f(x)= .
14.若f(x)=x2+bx+c,对任意的x∈R,都有f(1+x)= f(1-x), 则f(sin 1)与 f(sin)的大小关系是 .
15. 已知函数f(x)=-3.
(1)求f(x)的定义域;(2)若x∈,求f(x)的值域.
16. 已知函数f(x)=1-2sin x.
(1)用“五点(画图)法”作出函数f(x)在x∈[0,2π]上的简图;
(2)若方程f(x)=a在x∈上有两个实根,求a的取值范围.
课时把关练
§5 正弦函数、余弦函数的图象与性质再认识
5.1 正弦函数的图象与性质再认识
参考答案
1.B 2.D 3.C 4.A 5.D 6.D 7.A 8.C 9.AC 10.BCD
11.∪
12.①③ 13.sin πx(答案不唯一) 14. f(sin 1)f(sin)
15.解:(1)由题意,知2sin x+1>0,即sin x,解得x∈,k∈Z,
所以f(x)的定义域为,k∈Z.
(2)当x∈时,sin x∈,2sin x+1∈[1,2],∈[-1,0],
所以f(x)的值域为[-4,-3].
16.解:(1)列表:
x | 0 | π | 2π | ||
f(x) | 1 | -1 | 1 | 3 | 1 |
作图如图所示.
(2)若方程f(x)=a在x∈上有两个实根,
则y=sin x与y=的图象在x∈上有两个不同的交点.
因为x∈,所以sin x∈[-1,1].
作出函数y=sin x在x∈上的图象,如图所示.
又=-,=-1,sin=,sin=1,
由图象可得-1<≤-或≤<1,故a的取值范围是(-1,0]∪[1+,3).
北师大版 (2019)必修 第二册第一章 三角函数5 正弦函数、余弦函数的图象与性质再认识5.2 余弦函数的图象与性质再认识获奖课件ppt: 这是一份北师大版 (2019)必修 第二册第一章 三角函数5 正弦函数、余弦函数的图象与性质再认识5.2 余弦函数的图象与性质再认识获奖课件ppt,共20页。
北师大版 (2019)必修 第二册第一章 三角函数5 正弦函数、余弦函数的图象与性质再认识5.2 余弦函数的图象与性质再认识优秀课件ppt: 这是一份北师大版 (2019)必修 第二册第一章 三角函数5 正弦函数、余弦函数的图象与性质再认识5.2 余弦函数的图象与性质再认识优秀课件ppt,共18页。
高中数学5.2 余弦函数的图象与性质再认识备课ppt课件: 这是一份高中数学5.2 余弦函数的图象与性质再认识备课ppt课件,共27页。













