






北师大版高中数学必修第一册5.2 实际问题中的函数模型课件+练习
展开同步练习
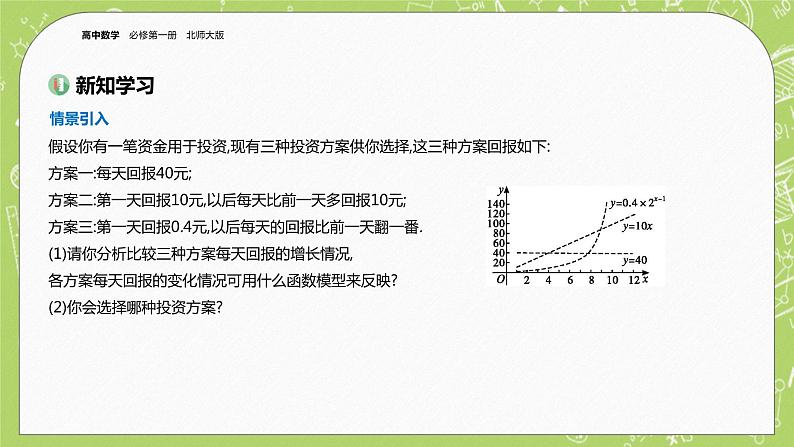
§2 实际问题中的函数模型
2.2 用函数模型解决实际问题
1.设某种蜡烛所剩长度(单位:厘米)与点燃时间(单位:分钟)的函数关系式是.若点燃6分钟后,蜡烛的长度为17.4厘米,点燃21分钟后,蜡烛的长度为8.4厘米,则这支蜡烛燃尽的时间为( )
A.21分钟 B.25分钟 C.30分钟 D.35分钟
2.某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为=2+21和=2,其中为销售量(单位:辆),若该公司在两地共销售15辆车,则能获得的最大利润为( )
A.120万元 B.120.25万元 C.114万元 D.118万元
3.加工爆米花时,爆开且不煳的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率与加工时间(单位:分钟)满足函数关系=2++(,,是常数),如图记录了三次数据,根据上述函数模型和数据,可得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟
4.若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过年后剩留量为,则,的函数关系是( )
A. B. 0.957 6100x C. = D.
5.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为=其中代表拟录用人数,代表面试人数.若面试人数为60,则该公司拟录用人数为( )
A.15 B.40 C.25 D.70
6.把物体放在冷空气中冷却,如果物体原来的温度是(单位:℃),空气的温度是(单位:℃),经过分钟后物体的温度(单位:℃)可由公式求得.把温度是90℃的物体放在10℃的空气中冷却分钟后,物体的温度是50℃,那么的值约为(参考数据:ln 3≈1.099,ln 2 ≈0.693)( )
A.1.78 B.2.77 C.2.89 D.4.40
7.要制作一个容积为4 m3,高为1 m的无盖长方体容器,已知该容器底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )
A.80元 B.120元 C.160元 D.240元
8.火箭的最大速度(单位:km/s)、燃料的质量(单位:kg)和火箭(除燃料外)的质量(单位:kg)的函数关系是=2 .若火箭的最大速度为11.2 km/s,则燃料质量与火箭质量(除燃料外)的比值约为( )(参考数据:e0.005 6≈1.005 6)
A. 1.005 6 B. 0.502 8 C. 0.005 6 D. 0.002 8
9.大学生甲利用业余时间在网上开了一家文具店,为积累客户,甲决定开展一次促销活动:每笔订单总价达到100元,客户就少付元.已知根据网站协议,每笔订单客户网上支付成功后,店家会得到支付款的80%.现为保证甲每笔订单得到的支付款金额不低于促销前总价的70%,则的最大值为 .
10.生产一定数量商品的全部费用称为生产成本,某企业一个月生产某种商品万件时的生产成本为()=2+2+20(单位:万元),商品的售价是每件20元,为获取最大利润(利润=收入-成本),该企业一个月应生产该商品的数量为 万件.
11.某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常.排气4分钟后测得车库内一氧化碳浓度为 64 ppm(ppm为浓度单位,1 ppm表示百万分之一),经检验知,该地下车库一氧化碳浓度(ppm)与排气时间(分钟)之间存在函数关系(为常数),可求得= ;若空气中一氧化碳浓度不高于0.5 ppm为正常,则至少需要排气 分钟才能使这个地下车库中一氧化碳含量达到正常状态.
12.某市科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值(值越大,产品的性能越好)与这种新合金材料的含量(单位:克)的关系为:当0≤7时,是的二次函数;当≥7时,=.测得部分数据如下表所示.
(单位:克) | 0 | 2 | 6 | 10 | … |
-4 | 8 | 8 |
| … |
(1)求关于的函数关系式;
(2)求该新合金材料的含量为何值时,产品的性能达到最佳.
§2 实际问题中的函数模型
2.2 用函数模型解决实际问题
参考答案
1.D 2.A 3.B 4.A 5.C 6.B 7.C 8.C
9.12.5 10.18 11. 32
12.解:(1)当0≤<7时,是的二次函数,可设=2++(≠0),由=0,=4,得=4,
由=2,=8,得=12①,
由=6,=8,得36+6=12②,
联立①②解得=1,=8,即=2+84(0≤<7);
当≥7时,=,由=10,=,可得=8,
即=(≥7).
综上可得=
(2)当0≤<7时,=2+84=(4)2+12,
当=4时,取得最大值12;
当≥7时,=单调递减,当=7时,取得最大值3.
综上可得,当=4时,产品的性能达到最佳.









