高中数学北师大版 (2019)必修 第一册3.2 基本不等式精品课件ppt

基本不等式

【学习目标】

1．通过两个探究实例，引导学生基本不等式，了解基本不等式的几何背景，体会数形结合的思想；

2．借助基本不等式解决简单的最值问题，

【学习难点】

1．基本不等式成立时的三个限制条件（简称一正、二定、三相等）；

2．利用基本不等式求解实际问题中的最大值和最小值。

【学习重点】

应用数形结合的思想证明基本不等式，并从不同角度探索基本不等式的证明过程及应用。

【学习过程】

一、自主预习

1．两个非负实数的算术平均值________它们的几何平均值

2．若，取，，，则：当且仅当时，等号成立这个不等式称为__________

3．当，均为正数时，下面的命题均成立：

（1）若（s为定值）则当且仅当时，取得最大值________

（2）若(p为定值）则当且仅当时，取得最小值_____

二、例题探究

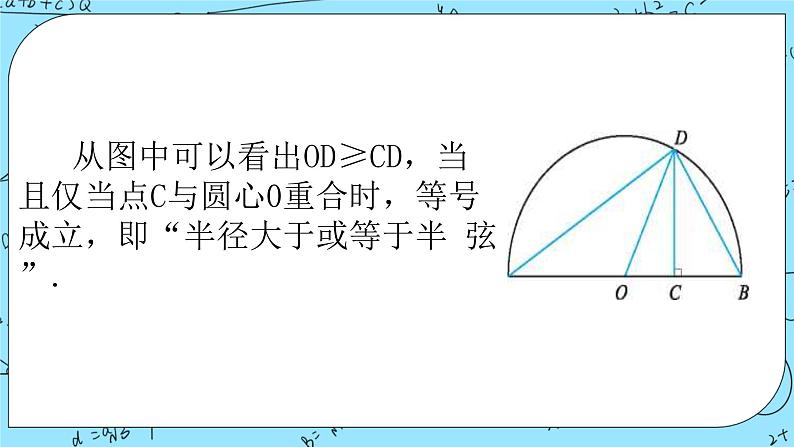
1．《几何原本》中的几何代数法（以几何方法研究代数问题）成为了后世数学家处理问题的重要依据．通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明．如图所示的图形，在AB上取一点C，使得，，过点C作交圆周于D，连接OD．作交OD于E．由可以证明的不等式为（  ）

A．

B．

C．

D．

2．若，，则的最小值为（  ）

A．2

B．

C．

D．

3．若矩形的周长1为定值，则该矩形的面积的最大值是（  ）

A．

B．

C．

D．

4．已知，，当时，不等式恒成立，则的取值范围是（  ）

A．

B．

C．

D．

【课后巩固】

1．下列命题中正确的是（  ）

A．若，则

B．若，则 

C．若，则

D．若，则

2．下列函数中，最小值是2的是（  ）

A．

B．

C．

D．

3．函数的最小值为（  ）

A．6

B．7

C．8

D．9

4．已知实数，且，则的最小值为（  ）

A．9 B． C．5 D．4

5．已知，则的最小值为（  ）

A．4 B．16 C．8 D．10

6．若正数a，b满足，则当ab取最小值时，b的值为（  ）

A． B． C． D．

7．已知，，则的最小值为（  ）

A．9

B．12

C．15

D．

8．已知正实数满足，则最小值为（  ）

A．8

B．9

C．10

D．11

9．（1）设，求函数的最大值；

（2）解关于的不等式．

10．如图，要设计一张矩形广告牌，该广告牌含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为，四周空白的宽度为，两栏之间的中缝空白的宽度为，设广告牌的高为．

（1）求广告牌的面积关于的函数；

（2）求广告牌的面积的最小值．

【答案解析】

1．【解析】解：由射影定理可知，即，由得，

故选：A．

2．【解析】解：，，

，

，

，，

，

当且仅当即时取“”，

故选：D．

3．【解析】解：设矩形ABCD的长为，宽为，则其周长为定值，即；

所以该矩形的面积为，

当且仅当时取得最大值是．

故选：C．

4．【解答】解：，，，

，

不等式恒成立，，

整理得，解得，即，

的取值范围为．

故选：B．

【课后巩固答案解析】

1．D

2．C

3．C

4．B

5．C

6．A

7．D

8．B

9．【解析】解：（1）设，函数，故当时，函数取得最大值为．

（2）关于的不等式，即．

当时，不等式即，不等式无解；

当时，不等式的解集为；

当时，不等式的解集为．

综上可得，当时，不等式的解集为，当时，不等式的解集为，当时，不等式的解集为．

10．【解析】解：（1）依题意广告牌的高为，则，

所以，且，

所以广告牌的面积．

（2）由（1）知，

，

当且仅当，即号成立．

所以，

广告牌的面积的最小值为61.25．