北京市西城区2023届高三数学二模试卷含答案

这是一份北京市西城区2023届高三数学二模试卷含答案，共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
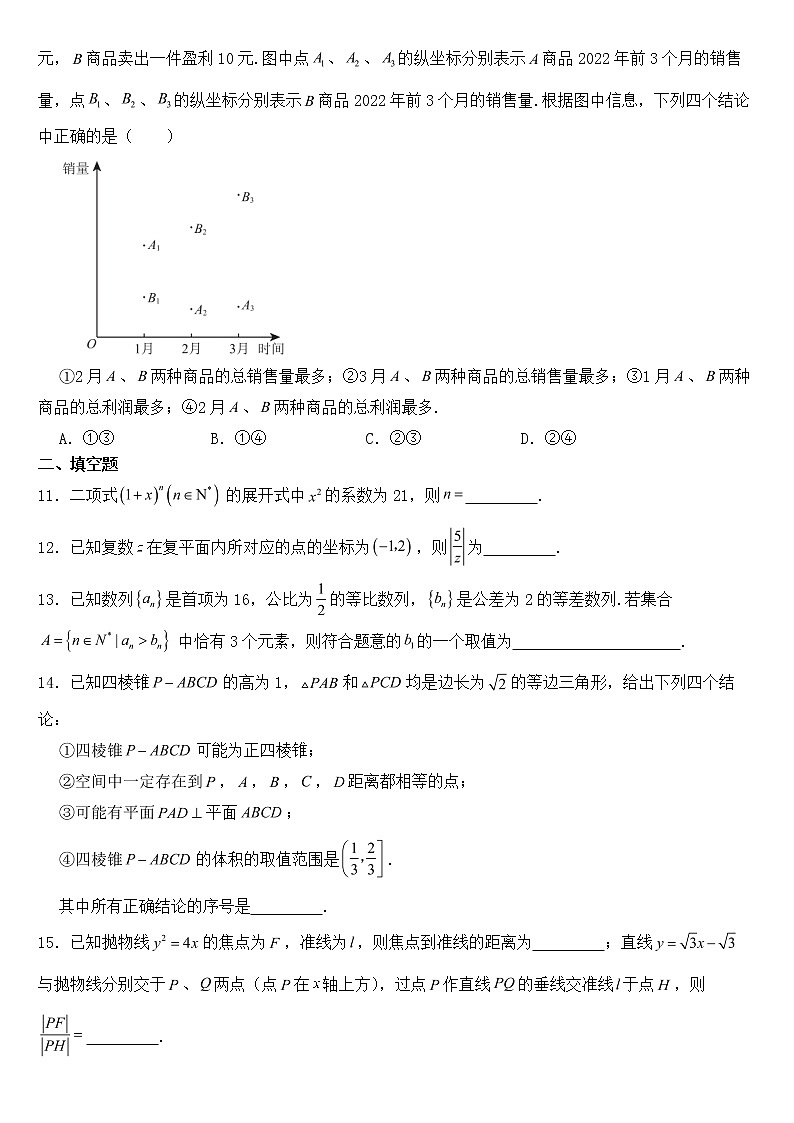
 高三数学二模试卷一、单选题1．已知集合，，则（　　）A． B． C． D．2．已知双曲线的焦点分别为，，，双曲线上一点满足，则该双曲线的离心率为（　　）A． B． C．2 D．33．已知为等差数列，首项，公差，若，则（　　）A．1 B．2 C．3 D．44．下列函数中，与函数的奇偶性相同，且在上有相同单调性的是（　　）A． B． C． D．5．已知直线与圆：交于，两点，且，则的值为（　　）A． B． C． D．26．已知是单位向量，向量满足，则的取值范围是（　　）A． B． C． D．7．已知函数，，那么“”是“在上是增函数”的（　　）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件8．已知，记关于的方程的所有实数根的乘积为，则（　　）A．有最大值，无最小值 B．有最小值，无最大值C．既有最大值，也有最小值 D．既无最大值，也无最小值9．若函数的定义域和值域的交集为空集，则正数的取值范围是（　　）A． B． C． D．10．如图为某商铺、两种商品在2022年前3个月的销售情况统计图，已知商品卖出一件盈利20元，商品卖出一件盈利10元.图中点、、的纵坐标分别表示商品2022年前3个月的销售量，点、、的纵坐标分别表示商品2022年前3个月的销售量.根据图中信息，下列四个结论中正确的是（　　）①2月、两种商品的总销售量最多；②3月、两种商品的总销售量最多；③1月、两种商品的总利润最多；④2月、两种商品的总利润最多.A．①③ B．①④ C．②③ D．②④二、填空题11．二项式的展开式中的系数为21，则　     　.12．已知复数在复平面内所对应的点的坐标为，则为　     　.13．已知数列是首项为16，公比为的等比数列，是公差为2的等差数列.若集合中恰有3个元素，则符合题意的的一个取值为　                 　.14．已知四棱锥的高为1，和均是边长为的等边三角形，给出下列四个结论：①四棱锥可能为正四棱锥；②空间中一定存在到，，，，距离都相等的点；③可能有平面平面；④四棱锥的体积的取值范围是.其中所有正确结论的序号是　     　.15．已知抛物线的焦点为，准线为，则焦点到准线的距离为　     　；直线与抛物线分别交于、两点（点在轴上方），过点作直线的垂线交准线于点，则　     　.三、解答题16．在中，.（1）求的大小；（2）若，证明：.17．2021年12月9日，《北京市义务教育体育与健康考核评价方案》发布.义务教育体育与健康考核评价包括过程性考核与现场考试两部分，总分值70分.其中过程性考核40分，现场考试30分.该评价方案从公布之日施行，分学段过渡、逐步推开.现场考试采取分类限选的方式，把内容划分了四类，必考、选考共设置22项考试内容.某区在九年级学生中随机抽取1100名男生和1000名女生作为样本进行统计调查，其中男生和女生选考乒乓球的比例分别为和，选考1分钟跳绳的比例分别为和.假设选考项目中所有学生选择每一项相互独立.（1）从该区所有九年级学生中随机抽取1名学生，估计该学生选考乒乓球的概率；（2）从该区九年级全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人中恰有2人选考1分钟跳绳的概率；（3）已知乒乓球考试满分8分.在该区一次九年级模拟考试中，样本中选考乒乓球的男生有60人得8分，40人得7.5分，其余男生得7分；样本中选考乒乓球的女生有40人得8分，其余女生得7分.记这次模拟考试中，选考乒乓球的所有学生的乒乓球平均分的估计值为，其中男生的乒乓球平均分的估计值为，试比较与的大小.（结论不需要证明）18．如图，在三棱柱中，四边形是边长为4的菱形，，点为棱上动点（不与，重合），平面与棱交于点.（1）求证：；（2）若，从条件①、条件②、条件③这三个条件中选择两个条件作为已知，求直线与平面所成角的正弦值.条件①：平面平面；条件②：；条件③：.19．已知函数.（1）若，求的值；（2）当时，①求证：有唯一的极值点；②记的零点为，是否存在使得？说明理由.20．已知椭圆：的左顶点为，圆：经过椭圆的上、下顶点.（1）求椭圆的方程和焦距；（2）已知，分别是椭圆和圆上的动点（，不在坐标轴上），且直线与轴平行，线段的垂直平分线与轴交于点，圆在点处的切线与轴交于点.求线段长度的最小值.21．已知数列：，，…，，其中是给定的正整数，且.令，，，，，.这里，表示括号中各数的最大值，表示括号中各数的最小值.（1）若数列：2，0，2，1，-4，2，求，的值；（2）若数列是首项为1，公比为的等比数列，且，求的值；（3）若数列是公差的等差数列，数列是数列中所有项的一个排列，求的所有可能值（用表示）.
 1．A2．C3．D4．D5．B6．C7．A8．D9．B10．C11．712．13．-1（答案不唯一）14．①②④15．2；16．（1）解：在中，∵，∴，∴，∴，∵，∴（2）证明：∵，∴．由余弦定理得①，∵，∴②，将②代入①，得，整理得，∴17．（1）解：样本中男生的人数为人，样本中女生的人数为人，设从该区所有九年级学生中随机抽取1名学生，该学生选考乒乓球为事件，则该学生选考乒乓球的概率（2）解：设从该区九年级全体男生中随机抽取1人，选考跳绳为事件，从该区九年级全体女生中随机抽取1人，选考跳绳为事件，由题意，则从该区九年级全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人中恰有2人选考1分钟跳绳的概率为（3）解：18．（1）证明：在三棱柱中，，又平面，平面，所以平面，又因为平面平面，所以.（2）解：选条件①②.连接，取中点，连接，.在菱形中，，所以为等边三角形.又因为为中点，所以，又因为平面平面，平面平面， 平面，且，所以平面，平面，所以.又因为，所以.以为原点，以、、为轴、轴、轴建立空间直角坐标系，则，，，，.所以，.设平面的一个法向量为，则，所以令，则，，故.又因为，设直线与平面所成角为，所以.所以直线与平面所成角的正弦值为.选条件②③.连接，取中点，连接，.在菱形中，，所以为等边三角形.又为中点，故，且.又因为，.所以，所以.又因为，所以平面.以下同选①②.选条件①③取中点，连接，.在中，因为，所以，且，.又因为平面平面，平面平面，所以平面.因为平面，所以.在中，.又因为，，所以，所以.以下同选①②.19．（1）解：因为，所以因为，所以（2）解：①的定义域是，令，则.设，因为在上单调递减，所以在上单调递减.因为，所以在上有唯一的零点，|所以有有唯一解，不妨设为.与的情况如下，+0-增极大值减所以有唯一的极值点.②由题意，，则若存在a，使，则，所以因为在单调递减，，则需，即，与已知矛盾.所以，不存在，使得.20．（1）解：依题意，，由，得，所以椭圆C的方程为：，焦距为（2）解：设，则，依题意，设，且，因，则线段AP的中点为，直线AP的斜率，则线段AP的中垂线方程为：， 令得点M的纵坐标，而，则，即，直线OQ的斜率，因此，圆O在点Q处的切线斜率为，切线方程为，令得点N的纵坐标，即，则有，当且仅当，即时取“=”，所以线段长度的最小值为21．（1）解：由题设，，，，则，，，，则，所以，（2）解：若数列任意两项均不相等，当时；当且时，，又，，此时；综上，，故，不合要求；要使，即存在且使，即，又，则，当，则，不合要求；当，则，满足题设；综上，.（3）解：由题设数列单调递增且，由（2）知：，根据题设定义，存在且，，则，由比数列中个项大，，同理，所以；又至少比数列中一项小，，同理，所以；综上，.令数列，下证各值均可取到，ⅰ、当，而数列递增，，且，此时，，，则；ⅱ、当时，，则，当且时，令，则，所以，，此时；ⅲ、给定，令()且()，则()，()，又数列递增，，()，()，所以，此时且，故，综上，.