人教版八年级下册18.2.2 菱形第4课时课后复习题

18.2 特殊的平行四边形

第4课时 菱形的判定

基础训练

知识点1 由对角线的位置关系判定菱形

1.(2016·齐齐哈尔)如图,▱ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件__________使其成为菱形(只填一个即可). 

2.下列命题中正确的是(　　)

A.对角线相等的四边形是菱形

B.对角线互相垂直的四边形是菱形

C.对角线相等的平行四边形是菱形

D.对角线互相垂直平分的四边形是菱形

3.如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是(　　)

A.BA=BC B.AC,BD互相平分

C.AC=BD D.AB∥CD

4.在▱ABCD中,下列结论不一定正确的是(　　)

A.AC=BD

B.当AC⊥BD时,它是菱形

C.当AC=BD时,它是矩形

D.AB=CD

知识点2 由边的数量关系判定菱形

5.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.

从中选择一个条件使四边形BECF是菱形,你认为这个条件

是__________.(只填写序号) 

6.(2016·遵义)如图,在▱ABCD中,对角线AC与BD交于点O,若增加一个条件,使▱ABCD成为菱形,下列给出的条件不正确的是(　　)

A.AB=AD B.AC⊥BD

C.AC=BD D.∠BAC=∠DAC

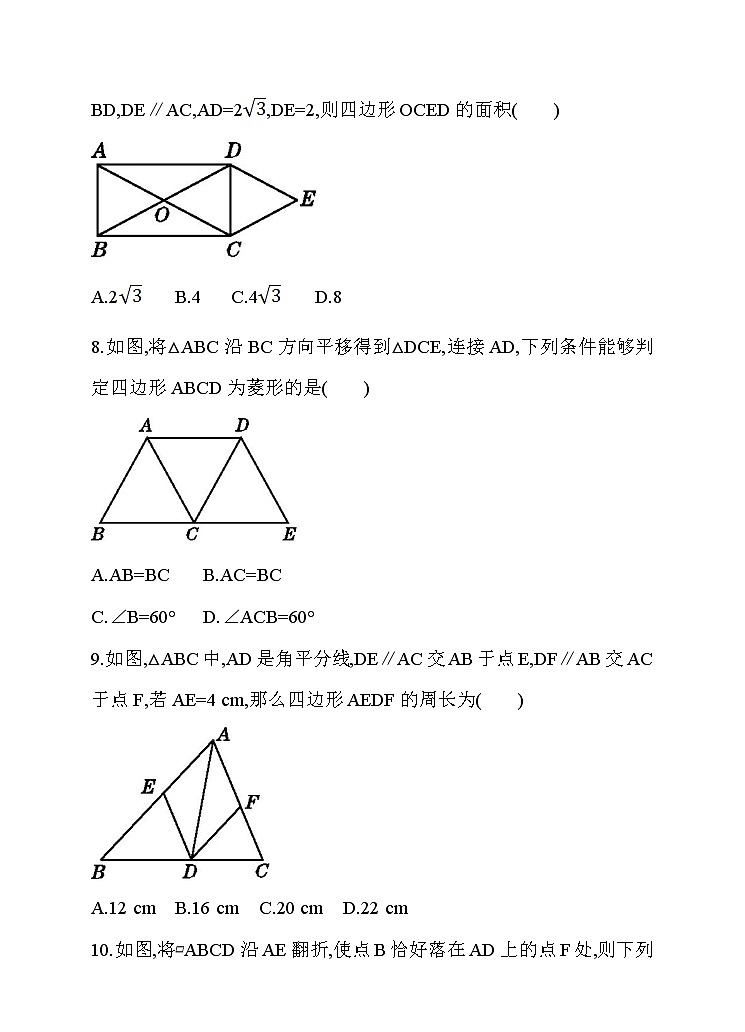
7.(2016·兰州)如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2,DE=2,则四边形OCED的面积(　　)

A.2    B.4    C.4    D.8

8.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是(　　)

A.AB=BC    B.AC=BC

C.∠B=60° D.∠ACB=60°

9.如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,若AE=4 cm,那么四边形AEDF的周长为(　　)

A.12 cm B.16 cm C.20 cm D.22 cm

10.如图,将▱ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是(　　)

A.AF=EF        B.AB=EF

C.AE=AF        D.AF=BE

易错点 臆造菱形的判定方法导致出错

11.下列命题:

①四边都相等的四边形是菱形;

②两组邻边分别相等的四边形是菱形;

③对角线互相垂直的平行四边形是菱形;

④对角线相等的四边形是菱形;

⑤一条对角线平分一组对角的平行四边形是菱形.

其中正确的是　　　　　.(填序号) 

提升训练

考查角度1 利用边的数量关系判定菱形

12.(2016·聊城)如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.

求证:四边形ADCF是菱形.

考查角度2 利用对角线的位置关系判定菱形

13.如图所示,AC是▱ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.

(1)求证:△AOE≌△COF;

(2)当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.

探究培优

拔尖角度1 利用菱形的判定解矩形问题

14.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;

(2)若AB=8,AD=16,求MD的长.

拔尖角度2 利用菱形的判定和性质探究满足条件的点的位置

15.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.

(1)证明:∠BAC=∠DAC,∠AFD=∠CFE;

(2)若AB∥CD,试证明四边形ABCD是菱形;

(3)在(2)的条件下,试确定点E的位置,使∠EFD=∠BCD,并说明理由.

参考答案

1.【答案】AC⊥BD(答案不唯一)

2.【答案】D　3.【答案】B

4.【答案】A　5.【答案】③

6.【答案】C　

解：根据菱形的定义可得,当AB=AD时▱ABCD是菱形,故A正确;

根据对角线互相垂直的平行四边形是菱形可得,当AC⊥BD时,▱ABCD是菱形,故B正确;

对角线相等的平行四边形是矩形,不一定是菱形,故C不正确;

当∠BAC=∠DAC时,在▱ABCD中,AD∥BC,∴∠ACB=∠DAC,

∴∠BAC=∠ACB,∴AB=BC,

∴▱ABCD是菱形.故D正确.

7.【答案】A　

解：如图,连接OE,与DC交于点F,易得四边形OCED为菱形,得到对角线互相平分且垂直,然后求出OE,DC的长,即可求出菱形OCED的面积.

8.【答案】A　9.【答案】B　10.【答案】C

11.错解:①②③⑤

诊断:②是最容易出错的,两组邻边分别相等的四边形不一定是菱形,如图,AB=AD,BC=CD,但四边形ABCD不是菱形.判定菱形时,要区分是在四边形还是平行四边形的基础上进行判定的,要注意两者的区别与联系.

正解:①③⑤

12.证明:∵AF∥CD,∴∠AFE=∠CDE.

∵E是AC的中点,∴AE=CE.

在△AFE和△CDE中,

∴△AFE≌△CDE(AAS).

∴AF=CD.

∵AF∥CD,

∴四边形ADCF是平行四边形.

∵∠B=90°,AC=2AB,

∴∠ACB=30°,∠BAC=60°.

∵AD平分∠BAC,

∴∠DAC=∠DAB=30°=∠ACD.

∴DA=DC.

∴四边形ADCF是菱形.

13.(1)证明:∵在▱ABCD中,AD∥BC,

∴∠EAO=∠FCO.

∵点O是AC的中点,

∴AO=CO.

又∵∠EOA=∠FOC,

∴△AOE≌△COF.

(2)解:当EF⊥AC时,四边形AFCE是菱形.理由如下:

由(1)知△AOE≌△COF,

∴OE=OF.

又∵AO=CO,

∴四边形AFCE是平行四边形.

∴当EF⊥AC时,四边形AFCE是菱形.

14.(1)证明:∵MN是BD的垂直平分线,

∴MB=MD,NB=ND,MN⊥BD.　

∴∠BMN=∠DMN.

又∵AD∥BC,∴∠DMN=∠BNM.

∴∠BMN=∠BNM.∴BM=BN.

∴BM=BN=ND=MD.

∴四边形BMDN是菱形.

(2)解:∵MB=MD,设MD的长为x,则MB=x,在Rt△AMB

中,BM2=AM2+AB2,即x2=(16-x)2+82,

解得x=10.∴MD的长为10.

15.(1)证明:在△ABC和△ADC中,

∴△ABC≌△ADC(SSS).

∴∠BAC=∠DAC.

在△ABF和△ADF中,

∴△ABF≌△ADF(SAS).

∴∠AFB=∠AFD.∵∠AFB=∠CFE,∴∠AFD=∠CFE.

(2)证明:∵AB∥CD,∴∠BAC=∠ACD.又∵∠BAC=∠DAC,∴∠DAC=∠ACD.∴AD=CD.

又∵AB=AD,CB=CD,∴AB=CB=CD=AD.∴四边形ABCD是菱形.

(3)解:当BE⊥CD,即E为过B且和CD垂直的垂线与CD的交点时,∠EFD=∠BCD.

理由:∵四边形ABCD为菱形,

∴∠BCF=∠DCF.

在△BCF和△DCF中,

∴△BCF≌△DCF(SAS).

∴∠CBF=∠CDF.

∵BE⊥CD,

∴∠BEC=∠DEF=90°.

∴∠EFD=∠BCD.