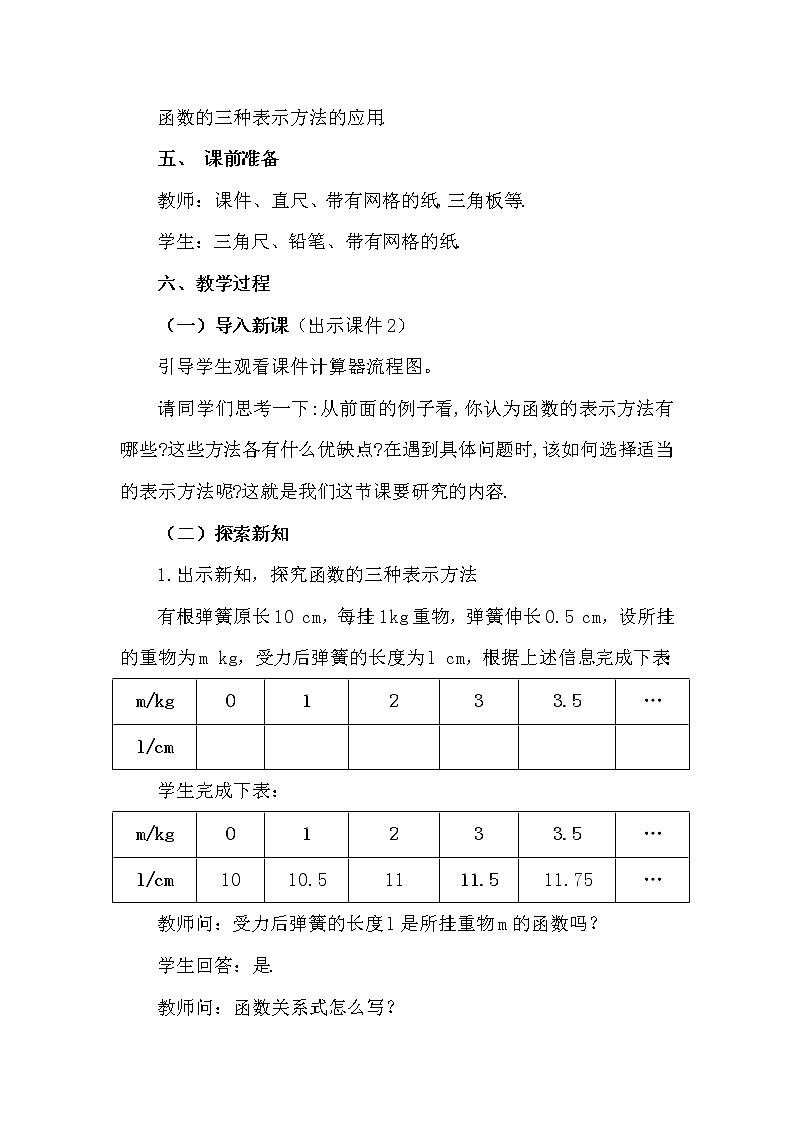
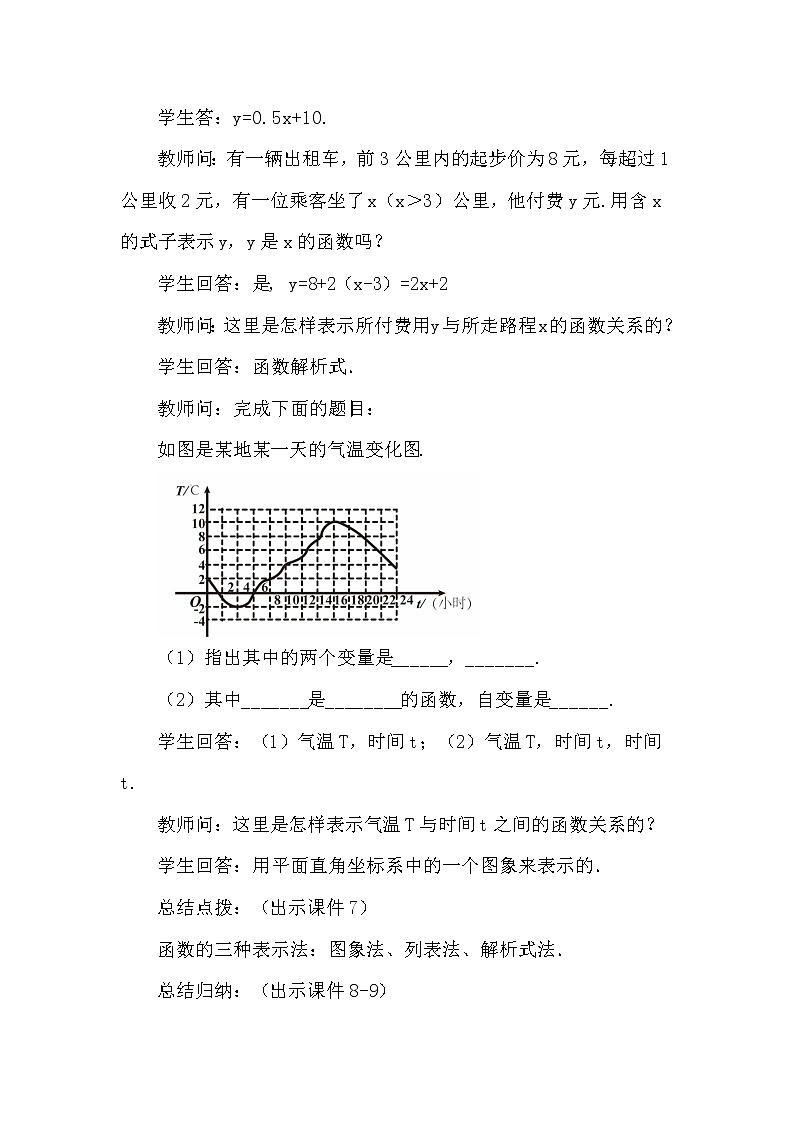
数学八年级下册19.1.2 函数的图象第2课时综合训练题

这是一份数学八年级下册19.1.2 函数的图象第2课时综合训练题，共9页。
19.1.2 函数的图象
第2课时一．     教学目标【知识与技能】1.运用丰富的实例,帮助学生全面理解函数的三种表示方法,进一步了解三种表示方法的优缺点.2.会根据具体情况选择适当方法表示函数.【过程与方法】1.通过作图、交流、归纳等数学活动,提高实际问题转化为数学问题的能力.2.会利用函数知识推测事物发展趋势的能力.【情感态度与价值观】让学生通过实际操作,体会函数三种表示法在实际生活中的应用价值,激发学生对数学学习的兴趣.二、     课型新授课三、课时第2课时 共2课时四、教学重难点【教学重点】 函数的三种表示方法及其应用.【教学难点】 函数的三种表示方法的应用.五、     课前准备 教师：课件、直尺、带有网格的纸,三角板等.学生：三角尺、铅笔、带有网格的纸.六、教学过程（一）导入新课（出示课件2）引导学生观看课件计算器流程图。请同学们思考一下:从前面的例子看,你认为函数的表示方法有哪些?这些方法各有什么优缺点?在遇到具体问题时,该如何选择适当的表示方法呢?这就是我们这节课要研究的内容.（二）探索新知1.出示新知，探究函数的三种表示方法有根弹簧原长10 cm，每挂1kg重物，弹簧伸长0.5 cm，设所挂的重物为m kg，受力后弹簧的长度为l cm，根据上述信息完成下表： m/kg01233.5…l/cm      学生完成下表： m/kg01233.5…l/cm1010.51111.511.75…教师问：受力后弹簧的长度l是所挂重物m的函数吗？学生回答：是.教师问：函数关系式怎么写？ 学生答：y=0.5x+10.教师问：有一辆出租车，前3公里内的起步价为8元，每超过1公里收2元，有一位乘客坐了x（x＞3）公里，他付费y元.用含x的式子表示y，y是x的函数吗？学生回答：是, y=8+2（x-3）=2x+2教师问：这里是怎样表示所付费用y与所走路程x的函数关系的？学生回答：函数解析式．教师问：完成下面的题目：如图是某地某一天的气温变化图.（1）指出其中的两个变量是______，_______.
    （2）其中_______是________的函数，自变量是______.学生回答：（1）气温T，时间t；（2）气温T，时间t，时间t.教师问：这里是怎样表示气温T与时间t之间的函数关系的？学生回答：用平面直角坐标系中的一个图象来表示的．总结点拨：（出示课件7）函数的三种表示法：图象法、列表法、解析式法．总结归纳：（出示课件8-9）函数的三种表示方法:(1)列表法：用表格列出自变量与函数的对应值，表示函数两个变量之间的关系，这种表示函数的方法叫做列表法.(2)图象法：用图象表示两个变量之间的函数关系，这种表示函数的方法叫做图象法.(3)解析式法：用数学式表示函数的方法叫做解析式法.请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点，填写下表：表示方法全面性准确性直观性形象性列表法×√√×解析式法√√××图象法××√√提示：从所填表中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时，就要根据具体情况选择适当的方法，有时为全面地认识问题，需要几种方法同时使用.考点1：函数表示方法的相互转化一水库的水位在最近5 h内持续上涨，下表记录了这5 h内6 个时间点的水位高度，其中 t 表示时间，y表示水位高度．（出示课件10-14）  t/h012345y/m33.33.63.94.24.5（1）在平面直角坐标系中描出表中数据对应的点，这些点是否在一条直线上？由此你发现水位变化有什么规律？ 学生回答：通过作图发现，这6个点在同一直线上，且每小时水位上升0.3m.由此猜想，在这个时间段中水位可能是以同一速度均匀上升的.（2）水位高度 y 是否为时间 t 的函数？如果是，试写出一个符合表中数据的函数解析式，并画出这个函数的图象．这个函数能表示水位的变化规律吗？学生回答：由于水位在最近5小时内持续上涨，对于时间t的每一个确定的值，水位高度y 都有唯一的值与其对应，所以，y是t 的函数.函数解析式为：y=0.3t+3. 变量的取值范围是：0≤t≤5.它表示在这5小时内，水位匀速上升的速度为0.3m/h，这个函数可以近似地表示水位的变化规律.
其函数的图象如下（3）据估计这种上涨规律还会持续2 h，预测再过2 h水位高度将达到多少m．学生回答：如果水位的变化规律不变，按上述函数预测，再持续2小时，水位的高度：5.1m.此时函数图象（线段AB）向右延伸到对应的位置，这时水位高度约为5.1m.出示课件15，学生自主练习后口答，教师订正.考点2：利用函数表达式解答实际问题如图，要做一个面积为12 m2的小花坛，该花坛的一边长为 x m，周长为 y m．（出示课件16-17）（1）变量y 是变量 x 的函数吗？如果是，写出自变量的取值范围；（2）能求出这个问题的函数解析式吗？（3）当 x 的值分别为1，2，3，4，5，6 时，请列表表示变量之间的对应关系；（4）能画出函数的图象吗？ 学生独立思考后，师生共同解答.解：（1）y 是 x 的函数，自变量 x 的取值范围是x＞0．（2）y =2（x+）.　（3）x/m123456y/m2616141414.816 出示课件18，学生自主练习后口答，教师订正.（三）课堂练习（出示课件19-31）教师引导学生练习课件第19-31相关题目，约用时20分钟。（四）课堂小结（出示课件32）  函数的表示方法列表法解析式法图象法概念通过列出自变量的值与对应函数值的表格来表示函数关系.用数学式子表示函数关系.把自变量与函数的每对对应值分别作为点的横、纵坐标，顺次连接这些点组成的图形，就是这个函数的图象．优点对表中已有自变量的每一个值，可一目了然地得出对应的函数值能准确地反映自变量与函数的对应关系能直观、形象地反映函数关系变化的趋势缺点列出对应值是有限的，不易得出自变量和函数之间的对应规律不是所有函数都能用函数解析式表示出来由自变量的值往往难以找到对应函数的准确值（五）课前预习预习下节课（19.2.1第1课时）的相关内容.知道正比例函数的定义和正比例函数的解析式.七、课后作业1、教材第81页练习第1,2,3题.2、七彩课堂第117-118页第3、6、8题.八、板书设计函数的图象第2课时1.函数的三种表示方法考点1  考点22.例题讲解九、教学反思本节课能力培养到位.设计上注重了数学思想方法在课堂中的渗透,领悟数学知识发生与发展过程中的思想方法;注重知识“结构化”的形成,帮助学生形成了知识体系,完善了认知结构.有效培养学生的发散思维能力和对知识的分析、归纳能力.在教学过程中,高估了学生的识图能力,主要的困难在于学生从图形获取信息的能力较弱,教学中对学生这方面的能力有所减弱.加强学生识图能力的教学,让学生多动手,多观察,熟练地从图形中获取信息.