江苏省苏州市5年（2018-2022）中考数学真题分类汇编-02选择题（提升题）知识点分类

这是一份江苏省苏州市5年（2018-2022）中考数学真题分类汇编-02选择题（提升题）知识点分类，共32页。试卷主要包含了已知点A等内容，欢迎下载使用。
江苏省苏州市5年（2018-2022）中考数学真题分类汇编-02选择题（提升题）知识点分类
一．分式的化简求值（共1小题）
1．已知两个不等于0的实数a、b满足a+b＝0，则+等于（　　）
A．﹣2 B．﹣1 C．1 D．2
二．由实际问题抽象出一元一次方程（共1小题）
2．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术，其中方程术是其最高的代数成就．《九章算术》中有这样一个问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步．若走路慢的人先走100步，走路快的人要走多少步才能追上？（注：步为长度单位）”设走路快的人要走x步才能追上，根据题意可列出的方程是（　　）
A．x＝100﹣x B．x＝100+x
C．x＝100+x D．x＝100﹣x
三．由实际问题抽象出二元一次方程组（共1小题）
3．某公司上半年生产甲、乙两种型号的无人机若干架，已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架．设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是（　　）
A．
B．
C．
D．
四．解一元一次不等式（共1小题）
4．不等式2x﹣1≤3的解集在数轴上表示正确的是（　　）
A． B．
C． D．
五．动点问题的函数图象（共1小题）
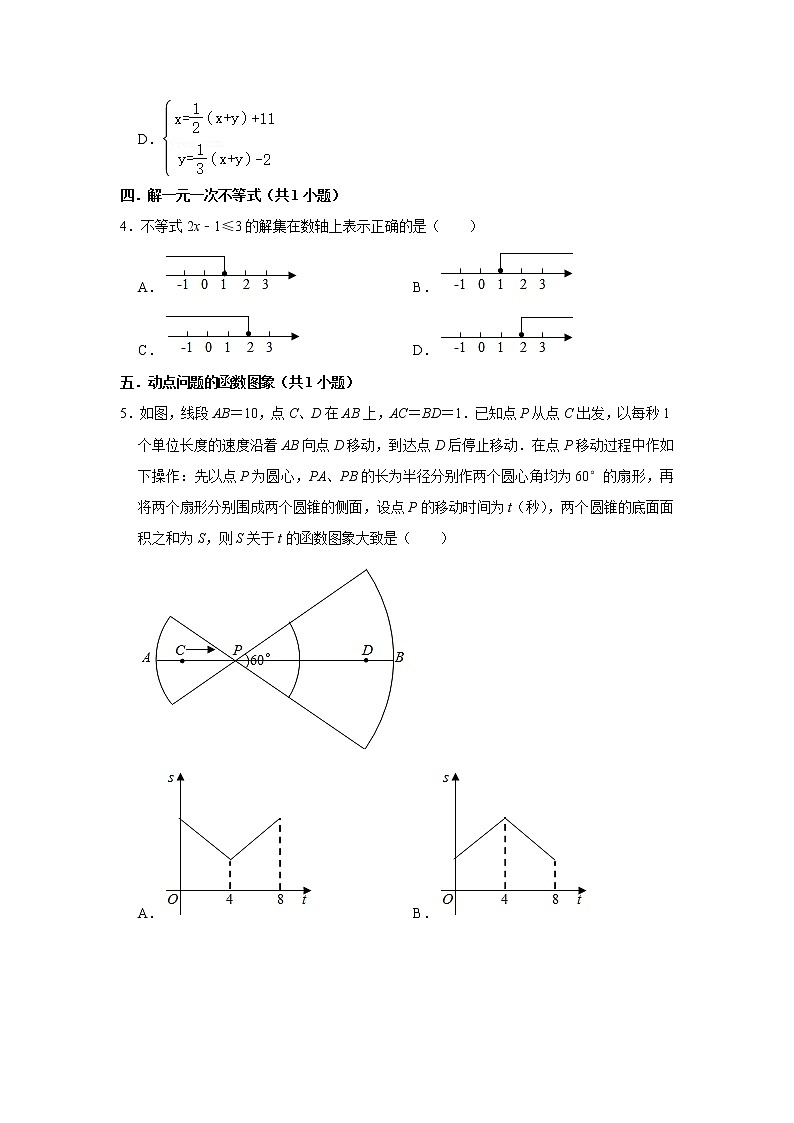
5．如图，线段AB＝10，点C、D在AB上，AC＝BD＝1．已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，PA、PB的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（　　）

A． B．
C． D．
六．一次函数图象上点的坐标特征（共1小题）
6．已知点A（，m），B（，n）在一次函数y＝2x+1的图象上，则m与n的大小关系是（　　）
A．m＞n B．m＝n C．m＜n D．无法确定
七．反比例函数系数k的几何意义（共1小题）
7．如图，平行四边形OABC的顶点A在x轴的正半轴上，点D（3，2）在对角线OB上，反比例函数y＝（k＞0，x＞0）的图象经过C、D两点．已知平行四边形OABC的面积是，则点B的坐标为（　　）

A．（4，） B．（，3） C．（5，） D．（，）
八．反比例函数图象上点的坐标特征（共1小题）
8．如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数y＝在第一象限内的图象经过点D，交BC于点E．若AB＝4，CE＝2BE，tan∠AOD＝，则k的值为（　　）

A．3 B．2 C．6 D．12
九．二次函数图象与几何变换（共1小题）
9．已知抛物线y＝x2+kx﹣k2的对称轴在y轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则k的值是（　　）
A．﹣5或2 B．﹣5 C．2 D．﹣2
一十．对顶角、邻补角（共1小题）
10．如图，直线AB与CD相交于点O，∠AOC＝75°，∠1＝25°，则∠2的度数是（　　）

A．25° B．30° C．40° D．50°
一十一．勾股定理（共1小题）
11．如图，点A的坐标为（0，2），点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转60°得到线段AC．若点C的坐标为（m，3），则m的值为（　　）

A． B． C． D．
一十二．三角形中位线定理（共1小题）
12．如图，在△ABC中，延长BC至D，使得CD＝BC，过AC中点E作EF∥CD（点F位于点E右侧），且EF＝2CD，连接DF．若AB＝8，则DF的长为（　　）

A．3 B．4 C．2 D．3
一十三．平行四边形的性质（共1小题）
13．如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线折叠得到△AB′C，B′C交AD于点E，连接B′D，若∠B＝60°，∠ACB＝45°，AC＝，则B′D的长是（　　）

A．1 B． C． D．
一十四．菱形的性质（共1小题）
14．如图，菱形ABCD的对角线AC，BD交于点O，AC＝4，BD＝16，将△ABO沿点A到点C的方向平移，得到△A'B'O'．当点A'与点C重合时，点A与点B'之间的距离为（　　）

A．6 B．8 C．10 D．12
一十五．圆周角定理（共1小题）
15．如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC＝40°，则∠D的度数为（　　）

A．100° B．110° C．120° D．130°
一十六．切线的性质（共1小题）
16．如图，AB为⊙O的切线，切点为A，连接AO、BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（　　）

A．54° B．36° C．32° D．27°
一十七．扇形面积的计算（共1小题）
17．如图，在扇形OAB中，已知∠AOB＝90°，OA＝，过的中点C作CD⊥OA，CE⊥OB，垂足分别为D、E，则图中阴影部分的面积为（　　）

A．π﹣1 B．﹣1 C．π﹣ D．﹣
一十八．旋转的性质（共2小题）
18．如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是（　　）

A． B．
C． D．
19．如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB'C'．若点B'恰好落在BC边上，且AB'＝CB'，则∠C'的度数为（　　）

A．18° B．20° C．24° D．28°
一十九．相似三角形的判定与性质（共1小题）
20．如图，在△ABC中，点D为BC边上的一点，且AD＝AB＝2，AD⊥AB．过点D作DE⊥AD，DE交AC于点E．若DE＝1，则△ABC的面积为（　　）

A．4 B．4 C．2 D．8
二十．解直角三角形的应用-仰角俯角问题（共2小题）
21．如图，小亮为了测量校园里教学楼AB的高度，将测角仪CD竖直放置在与教学楼水平距离为18m的地面上，若测角仪的高度是1.5m．测得教学楼的顶部A处的仰角为30°．则教学楼的高度是（　　）

A．55.5m B．54m C．19.5m D．18m
22．如图，小明想要测量学校操场上旗杆AB的高度，他做了如下操作：
（1）在点C处放置测角仪，测得旗杆顶的仰角∠ACE＝α；
（2）量得测角仪的高度CD＝a；
（3）量得测角仪到旗杆的水平距离DB＝b．
利用锐角三角函数解直角三角形的知识，旗杆的高度可表示为（　　）

A．a+btanα B．a+bsinα C．a+ D．a+
二十一．解直角三角形的应用-方向角问题（共1小题）
23．如图，某海监船以20海里/小时的速度在某海域执行巡航任务，当海监船由西向东航行至A处时，测得岛屿P恰好在其正北方向，继续向东航行1小时到达B处，测得岛屿P在其北偏西30°方向，保持航向不变又航行2小时到达C处，此时海监船与岛屿P之间的距离（即PC的长）为（　　）

A．40海里 B．60海里 C．20海里 D．40海里
二十二．算术平均数（共1小题）
24．为增强学生的环保意识，共建绿色文明校园，某学校组织“废纸宝宝旅行记”活动．经统计，七年级5个班级一周回收废纸情况如表：
班级
一班
二班
三班
四班
五班
废纸重量（kg）
4.5
4.4
5.1
3.3
5.7
则每个班级回收废纸的平均重量为（　　）
A．5kg B．4.8kg C．4.6kg D．4.5kg
二十三．几何概率（共2小题）
25．如图，在5×6的长方形网格飞镖游戏板中，每块小正方形除颜色外都相同，小正方形的顶点称为格点，扇形OAB的圆心及弧的两端均为格点．假设飞镖击中每一块小正方形是等可能的（击中扇形的边界或没有击中游戏板，则重投1次），任意投掷飞镖1次，飞镖击中扇形OAB（阴影部分）的概率是（　　）

A． B． C． D．
26．如图，飞镖游戏板中每一块小正方形除颜色外都相同．若某人向游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是（　　）

A． B． C． D．

江苏省苏州市5年（2018-2022）中考数学真题分类汇编-02选择题（提升题）知识点分类
参考答案与试题解析
一．分式的化简求值（共1小题）
1．已知两个不等于0的实数a、b满足a+b＝0，则+等于（　　）
A．﹣2 B．﹣1 C．1 D．2
【分析】方法一：先把所求式子通分，然后将分子变形，再根据两个不等于0的实数a、b满足a+b＝0，可以得到ab≠0，再将a+b＝0代入化简后的式子即可解答本题．
方法二：根据a+b＝0，得到a＝﹣b，然后代入所求式子，即可得到所求式子的值．
【解答】解：方法一：+
＝
＝
＝，
∵两个不等于0的实数a、b满足a+b＝0，
∴ab≠0，
当a+b＝0时，原式＝＝﹣2，
故选：A．
方法二：∵两个不等于0的实数a、b满足a+b＝0，
∴a＝﹣b，
∴+
＝
＝﹣1+（﹣1）
＝﹣2，
故选：A．
【点评】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
二．由实际问题抽象出一元一次方程（共1小题）
2．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术，其中方程术是其最高的代数成就．《九章算术》中有这样一个问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步．若走路慢的人先走100步，走路快的人要走多少步才能追上？（注：步为长度单位）”设走路快的人要走x步才能追上，根据题意可列出的方程是（　　）
A．x＝100﹣x B．x＝100+x
C．x＝100+x D．x＝100﹣x
【分析】设走路快的人要走x步才能追上，由走路快的人走x步所用时间内比走路慢的人多行100步，即可得出关于x的一元一次方程，此题得解．
【解答】解：设走路快的人要走x步才能追上，则走路慢的人走×60，
依题意，得：×60+100＝x．
故选：B．
【点评】本题考查了由实际问题抽象出一元一次方程以及数学常识，找准等量关系，正确列出一元一次方程是解题的关键．
三．由实际问题抽象出二元一次方程组（共1小题）
3．某公司上半年生产甲、乙两种型号的无人机若干架，已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架．设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是（　　）
A．
B．
C．
D．
【分析】设甲种型号无人机x架，乙种型号无人机y架，根据“甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架”列出方程组，此题得解．
【解答】解：设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是：．
故选：D．
【点评】此题主要考查了由实际问题抽象出二元一次方程组，列方程组解应用题的关键是找准等量关系．
四．解一元一次不等式（共1小题）
4．不等式2x﹣1≤3的解集在数轴上表示正确的是（　　）
A． B．
C． D．
【分析】先求出不等式的解集，再在数轴上表示出来即可．
【解答】解：移项得，2x≤3+1，
合并同类项得，2x≤4，
x的系数化为1得，x≤2．
在数轴上表示为：
．
故选：C．
【点评】本题考查的是在数轴上表示不等式的解集，熟知实心点与空心点的区别是解答此题的关键．
五．动点问题的函数图象（共1小题）
5．如图，线段AB＝10，点C、D在AB上，AC＝BD＝1．已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，PA、PB的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（　　）

A． B．
C． D．
【分析】先用t的代数式表示出两个扇形的半径，根据扇形的弧长等于底面圆的周长求出两个圆锥底面圆的半径，最后列出两个圆锥底面积之和关于t的函数关系式，根据关系式即可判断出符合题意的函数图形．
【解答】解：∵AB＝10，AC＝BD＝1，
∴CD＝10﹣1﹣1＝8，
∵PC＝t，
∴AP＝t+1，PB＝8﹣t+1＝9﹣t，
设围成的两个圆锥底面圆半径分别为r和R则：
2πr＝；．
解得：r＝，R＝，
∴两个圆锥的底面面积之和为S＝
＝
＝，
根据函数关系式可以发现该函数图象是一个开口向上的二次函数．
故选：D．
【点评】本题考查的是动点图象问题，涉及到扇形、圆锥有关知识，解决此类问题关键是：弄清楚题意思列出函数关系式．
六．一次函数图象上点的坐标特征（共1小题）
6．已知点A（，m），B（，n）在一次函数y＝2x+1的图象上，则m与n的大小关系是（　　）
A．m＞n B．m＝n C．m＜n D．无法确定
【分析】根据点A（，m），B（，n）在一次函数y＝2x+1的图象上，可以求得m、n的值，然后即可比较出m、n的大小，本题得以解决．
【解答】解：∵点A（，m），B（，n）在一次函数y＝2x+1的图象上，
∴m＝2+1，n＝2×+1＝3+1＝4，
∵2+1＜4，
∴m＜n，
故选：C．
【点评】本题考查一次函数图象上点的坐标特征，解答本题的关键是求出m、n的值．
七．反比例函数系数k的几何意义（共1小题）
7．如图，平行四边形OABC的顶点A在x轴的正半轴上，点D（3，2）在对角线OB上，反比例函数y＝（k＞0，x＞0）的图象经过C、D两点．已知平行四边形OABC的面积是，则点B的坐标为（　　）

A．（4，） B．（，3） C．（5，） D．（，）
【分析】求出反比例函数y＝，设OB的解析式为y＝mx，由OB经过D（3，2），得出OB的解析式为y＝x，设C（a，），且a＞0，由平行四边形的性质得BC∥OA，S平行四边形OABC＝2S△OBC，则B（，），BC＝﹣a，代入面积公式即可得出结果．
【解答】解：∵反比例函数y＝（k＞0，x＞0）的图象经过点D（3，2），
∴2＝，
∴k＝6，
∴反比例函数y＝，
∵OB经过原点O，
∴设OB的解析式为y＝mx，
∵OB经过点D（3，2），
则2＝3m，
∴m＝，
∴OB的解析式为y＝x，
∵反比例函数y＝经过点C，
∴设C（a，），且a＞0，
∵四边形OABC是平行四边形，
∴BC∥OA，S平行四边形OABC＝2S△OBC，
∴点B的纵坐标为，
∵OB的解析式为y＝x，
∴B（，），
∴BC＝﹣a，
∴S△OBC＝××（﹣a），
∴2×××（﹣a）＝，
解得：a＝2或a＝﹣2（舍去），
∴B（，3），
故选：B．
解法2：∵反比例函数y＝（k＞0，x＞0）的图象经过点D（3，2），
∴2＝，
∴k＝6，
∴反比例函数y＝，
同上得：B（，），
∴BC＝﹣a，
∵平行四边形OABC的面积是，
∴（﹣a）×＝，
解得：a＝2或a＝﹣2（舍去），
∴B（，3），
故选：B．
【点评】本题考查了反比例函数图象上点的坐标特征、待定系数法求一次函数解析式、平行四边形的性质、三角形面积计算等知识，熟练掌握平行四边形的性质是解题的关键．
八．反比例函数图象上点的坐标特征（共1小题）
8．如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数y＝在第一象限内的图象经过点D，交BC于点E．若AB＝4，CE＝2BE，tan∠AOD＝，则k的值为（　　）

A．3 B．2 C．6 D．12
【分析】由tan∠AOD＝＝可设AD＝3a、OA＝4a，在表示出点D、E的坐标，由反比例函数经过点D、E列出关于a的方程，解之求得a的值即可得出答案．
【解答】解：∵tan∠AOD＝＝，
∴设AD＝3a、OA＝4a，
则BC＝AD＝3a，点D坐标为（4a，3a），
∵CE＝2BE，
∴BE＝BC＝a，
∵AB＝4，
∴点E（4+4a，a），
∵反比例函数y＝经过点D、E，
∴k＝12a2＝（4+4a）a，
解得：a＝或a＝0（舍），
则k＝12×＝3，
故选：A．
【点评】本题主要考查反比例函数图象上点的坐标特征，解题的关键是根据题意表示出点D、E的坐标及反比例函数图象上点的横纵坐标乘积都等于反比例系数k．
九．二次函数图象与几何变换（共1小题）
9．已知抛物线y＝x2+kx﹣k2的对称轴在y轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则k的值是（　　）
A．﹣5或2 B．﹣5 C．2 D．﹣2
【分析】根据抛物线平移规律写出新抛物线解析式，然后将（0，0）代入，求得k的值．
【解答】解：∵抛物线y＝x2+kx﹣k2的对称轴在y轴右侧，
∴x＝﹣＞0，
∴k＜0．
∵抛物线y＝x2+kx﹣k2＝（x+）²﹣．
∴将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线的表达式是：y＝（x+﹣3）²﹣+1，
∴将（0，0）代入，得0＝（0+﹣3）²﹣+1，
解得k1＝2（舍去），k2＝﹣5．
故选：B．
【点评】本题主要考查了二次函数图象与几何变换，二次函数的性质以及二次函数图象上点的坐标特征，解题的关键是写出平移后抛物线解析式．
一十．对顶角、邻补角（共1小题）
10．如图，直线AB与CD相交于点O，∠AOC＝75°，∠1＝25°，则∠2的度数是（　　）

A．25° B．30° C．40° D．50°
【分析】先求出∠BOD的度数，再根据角的和差关系得结论．
【解答】解：∵∠AOC＝75°，
∴∠AOC＝∠BOD＝75°．
∵∠1＝25°，∠1+∠2＝∠BOD，
∴∠2＝∠BOD﹣∠1
＝75°﹣25°
＝50°．
故选：D．

【点评】本题考查了角的和差关系，掌握“对顶角相等”是解决本题的关键．
一十一．勾股定理（共1小题）
11．如图，点A的坐标为（0，2），点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转60°得到线段AC．若点C的坐标为（m，3），则m的值为（　　）

A． B． C． D．
【分析】过C作CD⊥x轴于点D，CE⊥y轴于点E，根据将线段AB绕点A按逆时针方向旋转60°得到线段AC，可得△ABC是等边三角形，又A（0，2），C（m，3），即得AC＝＝BC＝AB，可得BD＝＝，OB＝＝，从而+＝m，即可解得m＝．
【解答】解：过C作CD⊥x轴于点D，CE⊥y轴于点E，如图：

∵CD⊥x轴，CE⊥y轴，∠DOE＝90°，
∴四边形EODC是矩形，
∵将线段AB绕点A按逆时针方向旋转60°得到线段AC，
∴AB＝AC，∠BAC＝60°，
∴△ABC是等边三角形，
∴AB＝AC＝BC，
∵A（0，2），C（m，3），
∴CE＝m＝OD，CD＝3，OA＝2，
∴AE＝OE﹣OA＝CD﹣OA＝1，
∴AC＝＝＝BC＝AB，
在Rt△BCD中，BD＝＝＝，
在Rt△AOB中，OB＝＝＝，
∵OB+BD＝OD＝m，
∴+＝m，
化简变形得：3m4﹣22m2﹣25＝0，
解得m＝或m＝﹣（舍去），
∴m＝，
故选：C．
【点评】本题考查直角坐标系中的旋转变换，解题的关键是熟练应用勾股定理，用含m的代数式表示相关线段的长度．
一十二．三角形中位线定理（共1小题）
12．如图，在△ABC中，延长BC至D，使得CD＝BC，过AC中点E作EF∥CD（点F位于点E右侧），且EF＝2CD，连接DF．若AB＝8，则DF的长为（　　）

A．3 B．4 C．2 D．3
【分析】取BC的中点G，连接EG，根据三角形的中位线定理得：EG＝4，设CD＝x，则EF＝BC＝2x，证明四边形EGDF是平行四边形，可得DF＝EG＝4．
【解答】解：取BC的中点G，连接EG，
∵E是AC的中点，
∴EG是△ABC的中位线，
∴EG＝AB＝＝4，
设CD＝x，则EF＝BC＝2x，
∴BG＝CG＝x，
∴EF＝2x＝DG，
∵EF∥CD，
∴四边形EGDF是平行四边形，
∴DF＝EG＝4，
故选：B．

【点评】本题考查了平行四边形的判定和性质、三角形中位线定理，作辅助线构建三角形的中位线是本题的关键．
一十三．平行四边形的性质（共1小题）
13．如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线折叠得到△AB′C，B′C交AD于点E，连接B′D，若∠B＝60°，∠ACB＝45°，AC＝，则B′D的长是（　　）

A．1 B． C． D．
【分析】首先根据平行四边形的性质得AD∥BC，AB∥CD，可证出∠CAE＝45°，∠ADC＝60°，根据翻折可得∠ACB′＝∠ACB＝45°，∠AB′C＝∠B＝60°，进而可得∠AEC＝90°，从而可得AE＝CE＝，再根据含30°角的直角三角形的性质求出B′E＝DE＝1，根据勾股定理即可得B′D的长．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，∠ADC＝60°，
∴∠CAE＝∠ACB＝45°，
∵将△ABC沿AC翻折至△AB′C，
∴∠ACB′＝∠ACB＝45°，∠AB′C＝∠B＝60°，
∴∠AEC＝180°﹣∠CAE﹣∠ACB′＝90°，
∴AE＝CE＝AC＝，
∵∠AEC＝90°，∠AB′C＝60°，∠ADC＝60°，
∴∠B′AD＝30°，∠DCE＝30°，
∴B′E＝DE＝1，
∴B′D＝＝．
故选：B．
【点评】此题主要考查了平行四边形的性质，翻折的性质，勾股定理的应用，关键是熟练掌握平行四边形的性质．
一十四．菱形的性质（共1小题）
14．如图，菱形ABCD的对角线AC，BD交于点O，AC＝4，BD＝16，将△ABO沿点A到点C的方向平移，得到△A'B'O'．当点A'与点C重合时，点A与点B'之间的距离为（　　）

A．6 B．8 C．10 D．12
【分析】由菱形的性质得出AC⊥BD，AO＝OC＝AC＝2，OB＝OD＝BD＝8，由平移的性质得出O'C＝OA＝2，O'B'＝OB＝8，∠CO'B'＝90°，得出AO'＝AC+O'C＝6，由勾股定理即可得出答案．
【解答】解：∵四边形ABCD是菱形，
∴AC⊥BD，AO＝OC＝AC＝2，OB＝OD＝BD＝8，
∵△ABO沿点A到点C的方向平移，得到△A'B'O'，点A'与点C重合，
∴O'C＝OA＝2，O'B'＝OB＝8，∠CO'B'＝90°，
∴AO'＝AC+O'C＝6，
∴AB'＝＝＝10；
故选：C．
【点评】本题考查了菱形的性质、平移的性质、勾股定理；熟练掌握菱形的性质和平移的性质是解题的关键．
一十五．圆周角定理（共1小题）
15．如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC＝40°，则∠D的度数为（　　）

A．100° B．110° C．120° D．130°
【分析】根据互补得出∠AOC的度数，再利用圆周角定理解答即可．
【解答】解：∵∠BOC＝40°，
∴∠AOC＝180°﹣40°＝140°，
∴∠D＝，
故选：B．
【点评】此题考查圆周角定理，关键是根据互补得出∠AOC的度数．
一十六．切线的性质（共1小题）
16．如图，AB为⊙O的切线，切点为A，连接AO、BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（　　）

A．54° B．36° C．32° D．27°
【分析】由切线的性质得出∠OAB＝90°，由直角三角形的性质得出∠AOB＝90°﹣∠ABO＝54°，由等腰三角形的性质得出∠ADC＝∠OAD，再由三角形的外角性质即可得出答案．
【解答】解：∵AB为⊙O的切线，
∴∠OAB＝90°，
∵∠ABO＝36°，
∴∠AOB＝90°﹣∠ABO＝54°，
∵OA＝OD，
∴∠ADC＝∠OAD，
∵∠AOB＝∠ADC+∠OAD，
∴∠ADC＝∠AOB＝27°；
故选：D．
【点评】本题考查了切线的性质、直角三角形的性质、等腰三角形的性质以及三角形的外角性质；熟练掌握切线的性质和等腰三角形的性质是解题的关键．
一十七．扇形面积的计算（共1小题）
17．如图，在扇形OAB中，已知∠AOB＝90°，OA＝，过的中点C作CD⊥OA，CE⊥OB，垂足分别为D、E，则图中阴影部分的面积为（　　）

A．π﹣1 B．﹣1 C．π﹣ D．﹣
【分析】根据矩形的判定定理得到四边形CDOE是矩形，连接OC，根据全等三角形的性质得到OD＝OE，得到矩形CDOE是正方形，根据扇形和正方形的面积公式即可得到结论．
【解答】解：∵CD⊥OA，CE⊥OB，
∴∠CDO＝∠CEO＝∠AOB＝90°，
∴四边形CDOE是矩形，
连接OC，
∵点C是的中点，
∴∠AOC＝∠BOC，
∵OC＝OC，
∴△COD≌△COE（AAS），
∴OD＝OE，
∴矩形CDOE是正方形，
∵OC＝OA＝，
∴OE＝1，
∴图中阴影部分的面积＝﹣1×1＝﹣1，
故选：B．

【点评】本题考查了扇形面积的计算，正方形的判定和性质，全等三角形的判定和性质，正确识别图形是解题的关键．
一十八．旋转的性质（共2小题）
18．如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是（　　）

A． B．
C． D．
【分析】本题主要考查旋转的性质，旋转过程中图形形状和大小都不发生变化，根据旋转性质判断即可．
【解答】解：A选项是原图形的对称图形，故A不正确；
B选项是Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，故B正确；
C选项旋转后的对应点错误，即形状发生了改变，故C不正确；
D选项是按逆时针方向旋转90°，故D不正确；
故选：B．
【点评】本题主要考查旋转的性质，熟练掌握并应用旋转的性质是解题的关键，重点注意旋转的方向和角度．
19．如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB'C'．若点B'恰好落在BC边上，且AB'＝CB'，则∠C'的度数为（　　）

A．18° B．20° C．24° D．28°
【分析】由旋转的性质可得∠C＝∠C'，AB＝AB'，由等腰三角形的性质可得∠C＝∠CAB'，∠B＝∠AB'B，由三角形的外角性质和三角形内角和定理可求解．
【解答】解：∵AB'＝CB'，
∴∠C＝∠CAB'，
∴∠AB'B＝∠C+∠CAB'＝2∠C，
∵将△ABC绕点A按逆时针方向旋转得到△AB'C'，
∴∠C＝∠C'，AB＝AB'，
∴∠B＝∠AB'B＝2∠C，
∵∠B+∠C+∠CAB＝180°，
∴3∠C＝180°﹣108°，
∴∠C＝24°，
∴∠C'＝∠C＝24°，
故选：C．
【点评】本题考查了旋转的性质，等腰三角形的性质，灵活运用这些的性质解决问题是本题的关键．
一十九．相似三角形的判定与性质（共1小题）
20．如图，在△ABC中，点D为BC边上的一点，且AD＝AB＝2，AD⊥AB．过点D作DE⊥AD，DE交AC于点E．若DE＝1，则△ABC的面积为（　　）

A．4 B．4 C．2 D．8
【分析】由题意得到三角形DEC与三角形ABC相似，由相似三角形面积之比等于相似比的平方两三角形面积之比，进而求出四边形ABDE与三角形ABC面积之比，求出四边形ABDE面积，即可确定出三角形ABC面积．
【解答】解：∵AB⊥AD，AD⊥DE，
∴∠BAD＝∠ADE＝90°，
∴DE∥AB，
∴∠CED＝∠CAB，
∵∠C＝∠C，
∴△CED∽△CAB，
∵DE＝1，AB＝2，即DE：AB＝1：2，
∴S△DEC：S△ACB＝1：4，
∴S四边形ABDE：S△ACB＝3：4，
∵S四边形ABDE＝S△ABD+S△ADE＝×2×2+×2×1＝2+1＝3，
∴S△ACB＝4，
故选：B．
【点评】此题考查了相似三角形的判定与性质，以及等腰直角三角形，熟练掌握相似三角形的判定与性质是解本题的关键．
二十．解直角三角形的应用-仰角俯角问题（共2小题）
21．如图，小亮为了测量校园里教学楼AB的高度，将测角仪CD竖直放置在与教学楼水平距离为18m的地面上，若测角仪的高度是1.5m．测得教学楼的顶部A处的仰角为30°．则教学楼的高度是（　　）

A．55.5m B．54m C．19.5m D．18m
【分析】根据三角函数和直角三角形的性质解答即可．
【解答】解：过D作DE⊥AB，
∵在D处测得教学楼的顶部A的仰角为30°，
∴∠ADE＝30°，
∵BC＝DE＝18m，
∴AE＝DE•tan30°＝18m，
∴AB＝AE+BE＝AE+CD＝18+1.5＝19.5m，
故选：C．

【点评】此题考查了仰角的定义．注意能借助仰角构造直角三角形并解直角三角形是解此题的关键．
22．如图，小明想要测量学校操场上旗杆AB的高度，他做了如下操作：
（1）在点C处放置测角仪，测得旗杆顶的仰角∠ACE＝α；
（2）量得测角仪的高度CD＝a；
（3）量得测角仪到旗杆的水平距离DB＝b．
利用锐角三角函数解直角三角形的知识，旗杆的高度可表示为（　　）

A．a+btanα B．a+bsinα C．a+ D．a+
【分析】过C作CF⊥AB于F，则四边形BFCD是矩形，根据三角函数的定义即可得到结论．
【解答】解：过C作CF⊥AB于F，则四边形BFCD是矩形，
∴BF＝CD＝a，CF＝BD＝b，
∵∠ACF＝α，
∴tanα＝＝，
∴AF＝b•tanα，
∴AB＝AF+BF＝a+btanα，
故选：A．

【点评】本题主要考查解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的定义，并根据题意构建合适的直角三角形是解题的关键．
二十一．解直角三角形的应用-方向角问题（共1小题）
23．如图，某海监船以20海里/小时的速度在某海域执行巡航任务，当海监船由西向东航行至A处时，测得岛屿P恰好在其正北方向，继续向东航行1小时到达B处，测得岛屿P在其北偏西30°方向，保持航向不变又航行2小时到达C处，此时海监船与岛屿P之间的距离（即PC的长）为（　　）

A．40海里 B．60海里 C．20海里 D．40海里
【分析】首先证明PB＝BC，推出∠C＝30°，可得PC＝2PA，求出PA即可解决问题；
【解答】解：在Rt△PAB中，∵∠APB＝30°，
∴PB＝2AB，
由题意BC＝2AB，
∴PB＝BC，
∴∠C＝∠CPB，
∵∠ABP＝∠C+∠CPB＝60°，
∴∠C＝30°，
∴PC＝2PA，
∵PA＝AB•tan60°，
∴PC＝2×20×＝40（海里），
故选：D．
【点评】本题考查解直角三角形的应用﹣方向角问题，解题的关键是证明PB＝BC，推出∠C＝30°．
二十二．算术平均数（共1小题）
24．为增强学生的环保意识，共建绿色文明校园，某学校组织“废纸宝宝旅行记”活动．经统计，七年级5个班级一周回收废纸情况如表：
班级
一班
二班
三班
四班
五班
废纸重量（kg）
4.5
4.4
5.1
3.3
5.7
则每个班级回收废纸的平均重量为（　　）
A．5kg B．4.8kg C．4.6kg D．4.5kg
【分析】将五个班废纸回收质量相加，再除以5即可得出答案．
【解答】解：每个班级回收废纸的平均重量为×（4.5+4.4+5.1+3.3+5.7）＝4.6（kg），
故选：C．
【点评】本题主要考查算术平均数和统计表，解题的关键是掌握算术平均数的定义．
二十三．几何概率（共2小题）
25．如图，在5×6的长方形网格飞镖游戏板中，每块小正方形除颜色外都相同，小正方形的顶点称为格点，扇形OAB的圆心及弧的两端均为格点．假设飞镖击中每一块小正方形是等可能的（击中扇形的边界或没有击中游戏板，则重投1次），任意投掷飞镖1次，飞镖击中扇形OAB（阴影部分）的概率是（　　）

A． B． C． D．
【分析】根据几何概率的求法：飞镖落在阴影部分的概率就是阴影区域的面积与总面积的比值．
【解答】解：∵总面积为5×6＝30，其中阴影部分面积为＝，
∴飞镖落在阴影部分的概率是＝，
故选：A．
【点评】本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
26．如图，飞镖游戏板中每一块小正方形除颜色外都相同．若某人向游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是（　　）

A． B． C． D．
【分析】根据几何概率的求法：飞镖落在阴影部分的概率就是阴影区域的面积与总面积的比值．
【解答】解：∵总面积为3×3＝9，其中阴影部分面积为4××1×2＝4，
∴飞镖落在阴影部分的概率是，
故选：C．
【点评】本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/4/13 21:39:35；用户：19105418363；邮箱：19105418363；学号：36567650

菁优网APP 菁优网公众号 菁优网小程序