2023年九年级数学中考专题：二次函数综合压轴题（特殊四边形问题）附答案

这是一份2023年九年级数学中考专题：二次函数综合压轴题（特殊四边形问题）附答案，共16页。试卷主要包含了如图1，对于二次函数给出如下定义等内容，欢迎下载使用。
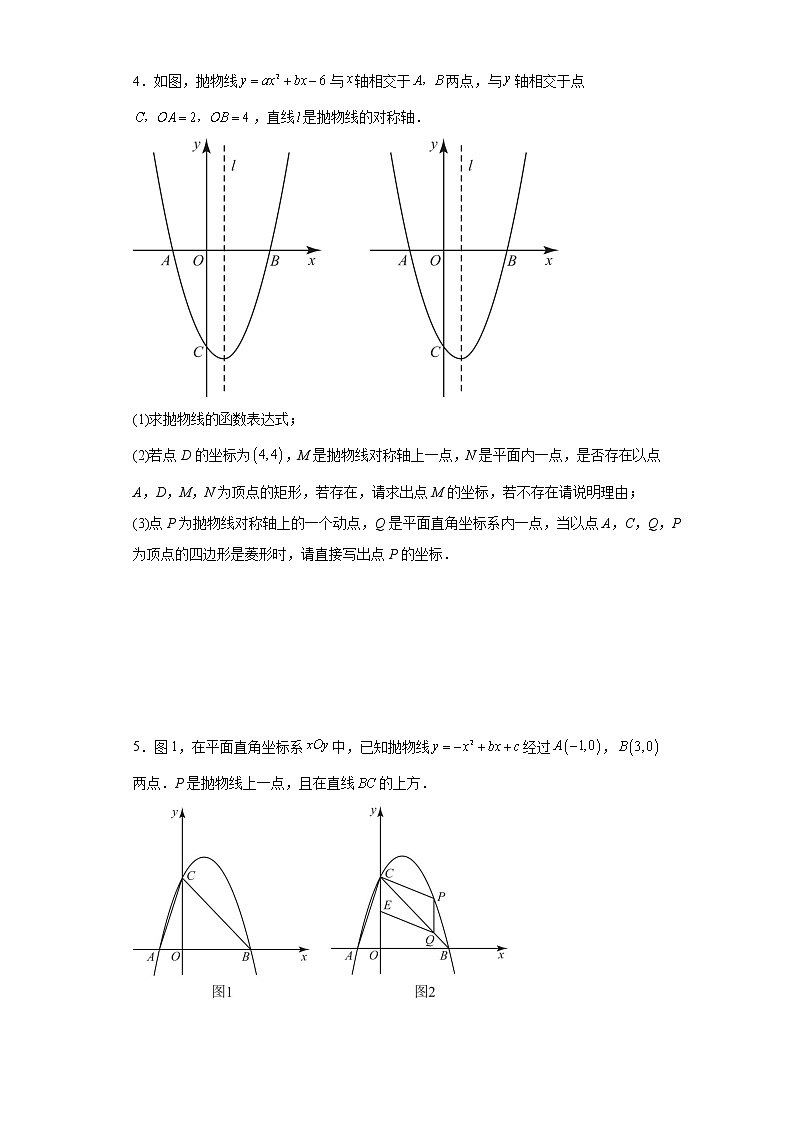
2023年九年级数学中考专题：二次函数综合压轴题（特殊四边形问题）附答案1．如图所示，在平面直角坐标系中，直线交坐标轴于B、C两点，抛物线经过B、C两点，且交x轴于另一点．点D为抛物线在第一象限内的一点，过点D作，交于点P，交x轴于点Q．(1)求抛物线的解析式；(2)设点P的横坐标为m，在点D的移动过程中，存在，求出m值；(3)在抛物线上取点E，在平面直角坐标系内取点F，问是否存在以C、B、E、F为顶点且以为边的矩形？如果存在，请求出点F的坐标；如果不存在，请说明理由．     2．抛物线经过、两点，且，直线过点，，点是线段（不含端点）上的动点，过作轴交抛物线于点，连接、．(1)求抛物线与直线的解析式；(2)求证：为定值；(3)在第四象限内是否存在一点，使得以、、、为顶点的平行四边形面积最大，若存在，求出点坐标；若不存在，请说明理由．      3．如图1．在平面直角坐标系中，抛物线与x轴交于点，点，与y轴交于点．(1)求抛物线的解析式；(2)点P是第一象限内的抛物线上一点．过点P作轴于点H，交直线BC于点Q，求的最大值，并求出此时点P的坐标；(3)如图2．将地物线沿射线BC的方向平移个单位长度．得到新抛物线，新抛物线与原抛物线交于点G，点M是x轴上一点，点N是新抛物线上一点，若以点C、G、M、N为顶点的四边形是平行四边形时，请直接写出点N的坐标．        4．如图，抛物线与轴相交于两点，与轴相交于点，直线是抛物线的对称轴．(1)求抛物线的函数表达式；(2)若点D的坐标为，M是抛物线对称轴上一点，N是平面内一点，是否存在以点A，D，M，N为顶点的矩形，若存在，请求出点M的坐标，若不存在请说明理由；(3)点P为抛物线对称轴上的一个动点，Q是平面直角坐标系内一点，当以点A，C，Q，P为顶点的四边形是菱形时，请直接写出点P的坐标．     5．图1，在平面直角坐标系中，已知抛物线经过，两点．P是抛物线上一点，且在直线的上方．(1)求抛物线的解析式；(2)如图2，点E为中点，作轴交于点Q，若四边形为平行四边形，求点P的横坐标；(3)如图3，连结，交于点M，作交于点H．记，，的面积分别为．判断是否存在最大值，若存在，求出最大值；若不存在，请说明理由．         6．在平面直角坐标系中，抛物线与轴的交点为，，与 轴交于点．(1)求抛物线的函数表达式；(2)如图1，连接，是第二象限内抛物线上一动点，过点作轴交直线于点，作轴交直线于点，求最大值以及此时点的坐标；(3)如图2，在（2）的条件下，将抛物线沿射线平移个单位，得到新抛物线，为新抛物线对称轴上一点，为新抛物线上一点，当以、、、为顶点的四边形是平行四边形时，请直接写出所有符合条件的点的坐标，并把求其中一个点的过程写出来．      7．如图，在平面直角坐标系中，抛物线与轴交于两点，与轴交于点，且．(1)试求抛物线的解析式；(2)直线与轴交于点，与抛物线在第一象限交于点，与直线交于点，连接，的面积记为，的面积记为，记，试求的最大值及此时点的坐标；(3)在（2）的条件下，取最大值时，点是轴上的一个动点，点是坐标平面内的一点，是否存在这样的点、，使得以四点组成的四边形是矩形？请直接写出满足条件的点的坐标．  8．对于二次函数给出如下定义：在平面直角坐标系中，二次函数，，为常数，且的图象顶点为（不与坐标原点重合），以为边构造正方形，则称正方形为二次函数的关联正方形，称二次函数为正方形的关联二次函数．若关联正方形的顶点落在二次函数图象上，则称此点为伴随点．(1)如图，直接写出二次函数的关联正方形顶点N的坐标___,并验证点N是否为伴随点___（填“是”或“否”）：(2)当二次函数的关联正方形的顶点与位于轴的两侧时，请解答下列问题：①若关联正方形的顶点、在轴的异侧时，求的取值范围：②当关联正方形的顶点是伴随点时，求关联函数的解析式；③关联正方形被二次函数图象的对称轴分成的两部分的面积分别为与，若，请直接写出的取值范围．    9．如图，直线与x轴交于点C，与y轴交于点B，抛物线经过B，C两点．(1)求抛物线的解析式；(2)点E是直线上方抛物线上的一动点，求面积的最大值及点E的坐标；(3)Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P，Q，B，C为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．       10．如图，在平面直角坐标系中，抛物线与x轴交于，两点，与y轴交于点C，且．(1)试求抛物线的解析式；(2)直线与y轴交于点D，与抛物线在第一象限交于点P，与直线交于点M，记，试求m的最大值及此时点P的坐标；(3)在（2）的条件下，m取最大值时，是否存在x轴上的点Q及坐标平面内的点N，使得P，D，Q，N四点组成的四边形是矩形？若存在，请直接写出所有满足条件的Q点和N点的坐标；若不存在，请说明理由．      11．如图1，抛物线与x轴相交于点A、B（点B在点A左侧），与y轴相交于点．已知点A坐标为，面积为6．(1)求抛物线的解析式；(2)点P是直线上方抛物线上一动点，过点P作直线的垂线，垂足为点E，过点P作轴交于点F，求周长的最大值及此时点P的坐标：(3)如图2，将该抛物线向左平移2个单位长度得到新的抛物线，平移后的抛物线与原抛物线相交于点D，点M为直线上的一点，点N是平面坐标系内一点，是否存在点M，N，使以点B，D，M，N为顶点的四边形为菱形，若存在，请直接写出点M的坐标；若不存在，请说明理由．       12．如图，抛物线与轴交于，两点，与轴交于点，顶点为．连接，，．(1)求抛物线的解析式；(2)求的面积；(3)若点在抛物线的对称轴上，抛物线上是否存在点，使得以，，，四点为顶点的四边形为平行四边形？若存在，求出满足条件的点的坐标；若不存在，请说明理由．      13．如图，抛物线经过点和点．(1)求抛物线解析式及顶点坐标；(2)设点是抛物线上一动点，且位于第一象限，四边形是以为对角线的平行四边形，求平行四边形的面积与之间的函数关系式；(3)当（2）中的平行四边形的面积为32时，请你判断平行四边形是否为菱形，并说明理由．          14．如图，抛物线与x轴交于A、B两点（A点在B点左侧）、直线与抛物线交于A、C两点，其中点C的横坐标为2．(1)求A、B两点的坐标及直线的函数表达式；(2)若点Р是线段上的一个动点，过点Р作y轴的平行线交抛物线于点E，求线段长度的最大值；(3)若点G是抛物线上的一个动点，在x轴上是否存在点F，使A、C、F、G这样的四个点为顶点的四边形是平行四边形？如果存在，直接写出所有满足条件的点F的坐标；如果不存在，请说明理由．       15．如图，一条顶点坐标为的抛物线与轴交于点，与轴交于点和点，有一宽度为，长度足够的矩形阴影部分沿轴方向平移，与轴平行的一组对边交抛物线于点和，交直线于点和，交轴于点和(1)求抛物线的解析式；(2)当点和都有在线段上时，连接，如果，求点的坐标；(3)在矩形的平移过程中，当以点，，，为顶点的四边形是平行四边形时，求点的坐标．      16．在如图所示的平面直角坐标系中，抛物线与x轴的交点为A、B．与y轴的交点为C．(1)请你求出点A、B、C的坐标并直接写出直线的关系式；(2)若点F是直线上方抛物线上的任意一点，连接、，请你求出面积的最大值；(3)点D在该抛物线的对称轴上，点E是平面直角坐标系内的任意一点，以点B、C、D、E为顶点的四边形是矩形，则点E的坐标是__________（请直接写出答案）        17．如图，抛物线与轴交于点、，与轴交于点，其顶点纵坐标为．(1)求的值；(2)求，两点的坐标；(3)以，为一组邻边作，则点关于轴的对称点是否在该抛物线上？请说明理由．      18．如图，抛物线与轴交于、，与轴交于．(1)求抛物线的解析式；(2)若点在抛物线上，且，求点的坐标；(3)已知线段与线段关于平面内某点成中心对称，其中的两端点刚好一个落在抛物线上，一个落在对称轴上，求出落在抛物线上的点的坐标．参考：若点、，则线段的中点坐标为．
参考答案：1．(1)(2)(3)存在，此时点的坐标为或 2．(1)；(2)见解析(3)存在， 3．(1)；(2)最大值为，此时点；(3)，或，或，或，． 4．(1)(2)存在，或或或(3)或或或或 5．(1)(2)(3)存在； 6．(1)(2)的最大值为；；(3)或或 7．(1)该抛物线的解析式为；(2)m的最大值为，此时点P的坐标为（2,4）；(3)N点的坐标为或． 8．(1)或；否(2)①或；②；③或且或 9．(1)(2)(3)点的坐标为或或 10．(1)(2)m最大值，点P的坐标为(3)存在，，；， 11．(1)(2)当时，的周长有最大值，为(3)点M的坐标为：或或或 12．(1)(2)3(3)，， 13．(1)，顶点坐标为．(2)；(3)见解析 14．(1)，，(2)(3)存在，，，，，， 15．(1)(2)(3)符合条件的点是，或 16．(1) ，，，；(2)；(3)或或或； 17．(1)(2)的坐标 ，的坐标 (3)在抛物线上，理由见解析 18．(1)(2)，，(3)或