2023年中考数学高频考点突破反比例函数与一次函数综合附答案

这是一份2023年中考数学高频考点突破反比例函数与一次函数综合附答案，共50页。

2023年中考数学高频考点突破——反比例函数与一次函数综合附答案
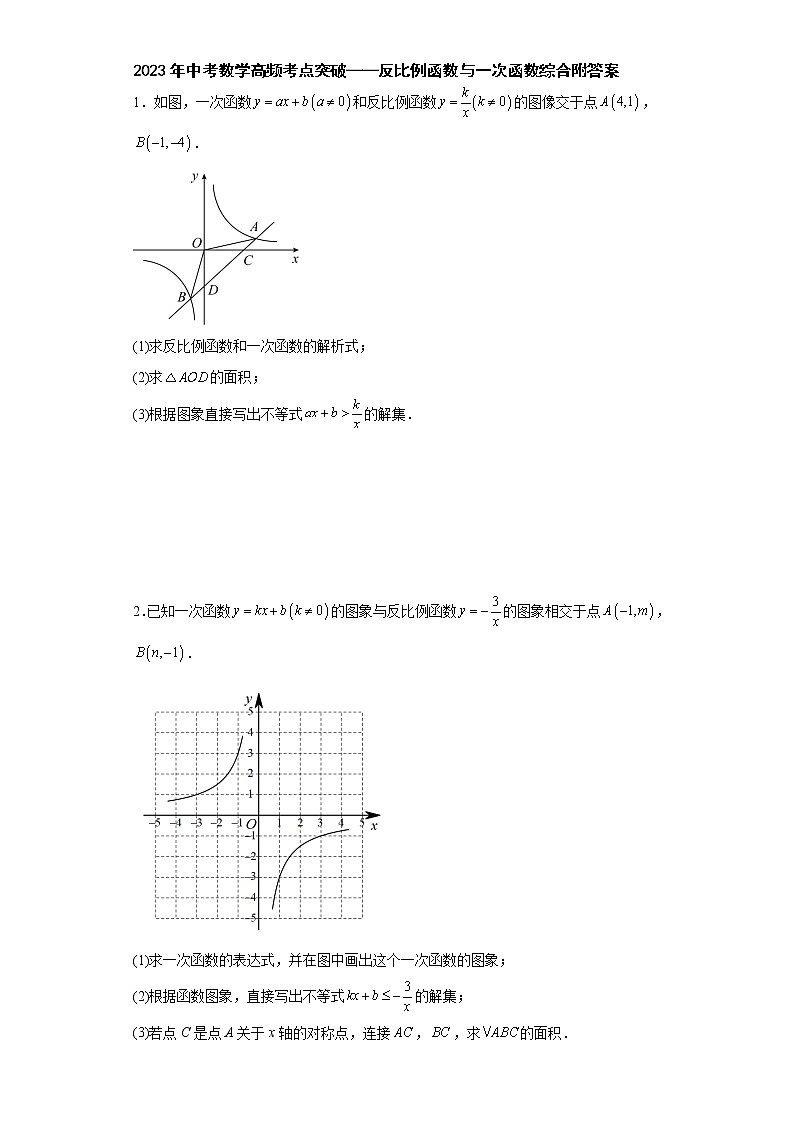
1．如图，一次函数和反比例函数的图像交于点，．

(1)求反比例函数和一次函数的解析式；
(2)求的面积；
(3)根据图象直接写出不等式的解集．





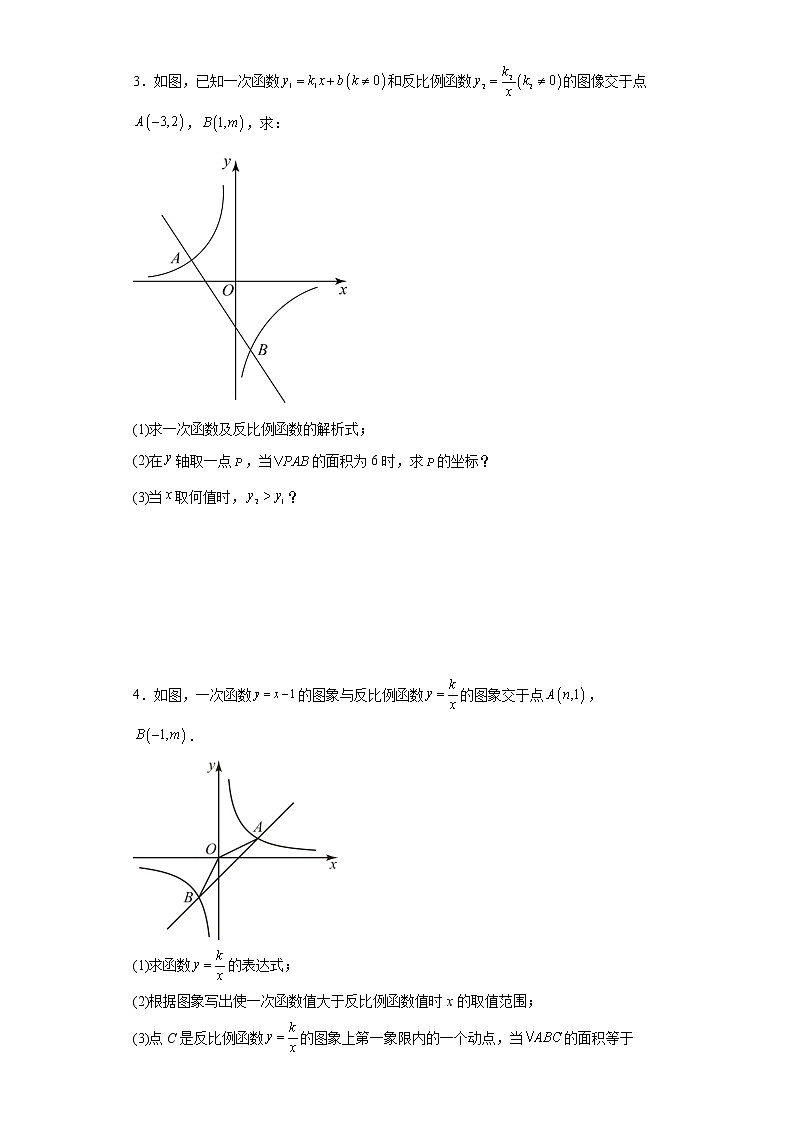
2．已知一次函数的图象与反比例函数的图象相交于点，．

(1)求一次函数的表达式，并在图中画出这个一次函数的图象；
(2)根据函数图象，直接写出不等式的解集；
(3)若点C是点A关于x轴的对称点，连接，，求的面积．
3．如图，已知一次函数和反比例函数的图像交于点，，求：

(1)求一次函数及反比例函数的解析式；
(2)在轴取一点，当的面积为6时，求的坐标？
(3)当取何值时，？





4．如图，一次函数的图象与反比例函数的图象交于点，．

(1)求函数的表达式；
(2)根据图象写出使一次函数值大于反比例函数值时x的取值范围；
(3)点C是反比例函数的图象上第一象限内的一个动点，当的面积等于的面积时，求C点的坐标．
5．如图，一次函数的图象与反比例函数的图象交于第二、四象限内的点和点．过点作x轴的垂线，垂足为点，的面积为3
(1)分别求出一次函数与反比例函数的表达式；
(2)结合图象直接写出的解集；
(3)在x轴正半轴上取点，使取得最大值时，求出点的坐标．






6．如图，点和是一次函数的图象与反比例函数的图象的两个交点．

(1)求反比例函数的表达式；
(2)设点P是y轴上的一个动点，当的周长最小时，求点P的坐标；
(3)在（2）的条件下，设点D是坐标平面内一个动点，当以点A，B，P，D为顶点的四边形是平行四边形时，请直接写出符合条件的所有点D的坐标．
7．如图，已知一次函数的图像经过点，且与x轴交于点M，反比例函数的图象经过点．

(1)若，求一次函数表达式；
(2)若一次函数y的值随x值的增大而增大，则m的取值范围是__________；
(3)若，求的面积．





8．如图，已知一次函数图象与反比例函数的图象交于两点，其中点坐标，点坐标．

(1)求一次函数及反比例函数的表达式；
(2)当时，直接写出的取值范围；
(3)若点为直线上一点，当时，求点的坐标．



9．在平面直角坐标系中，点D是反比例函数y=的一点，点D的纵坐标为6．

(1)当一次函数的图象与x轴交于点，与反比例函数y=的图象交于A，C两点，点是x轴上一定点，已知点A的纵坐标为4．求一次函数和反比例函数的解析式；
(2)在（1）的条件下，在线段AB上找点Q使得的面积为7时，求点Q的坐标；
(3)如图2，在第一象限内，在反比例函数上是否存在不同于点D的一点F，满足，且，若存在求出点D的坐标．若不存在，请说明理由．




10．如图，在平面直角坐标系中，一次函数的图象与反比例函数()的图象交于A，B两点，直线与x轴交于点C，点A的坐标为，点B的坐标为．

(1)求反比例函数和一次函数的解析式；
(2)求的面积；
(3)在x轴上是否存在一点P，使是直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
11．如图，一次函数的图像与反比例函数在第一象限的图像交于A（1，a）和B（b，1）两点，与x轴交于点C．

(1)求点B的坐标和反比例函数的关系式；
(2)直接写出当x＞0时，不等式的解集；
(3)若点P在y轴上，且△APB的面积为3，求点P的坐标．






12．已知一次函数与反比例函数的图像交于A(－4，3)、B(2，)两点．

(1)求一次函数和反比例函数的表达式；
(2)求AOB的面积；
(3)点P在轴上，当PAO为等腰三角形时，直接写出点P的坐标．



13．如图，一次函数y1＝﹣x+4与反比例函数y2＝（x＞0）的图象交于A，B两点．

(1)点A的坐标是______，点B的坐标是______：
(2)点P是直线AB上一点，设点P的横坐标为m．
①当y1＜y2时，m的取值范围是______；
②点P在线段AB上，过点P作PD⊥x轴于点D，连接OP．若△POD的面积最小时，求m的值．




14．如图，一次函数的图象与反比例函数的图象交于点，与y轴交于点B．

(1)求a，k的值；
(2)直线CD过点A，与反比例函数图象交于点C，与x轴交于点D，AC＝AD，连接CB．
①求△ABC的面积；
②点P在反比例函数的图象上，点Q在x轴上，若以点A，B，P，Q为顶点的四边形是平行四边形，请求出所有符合条件的点P坐标．


15．如图，一次函数y＝kx＋n的图像经过点和点，与x轴交于点C，反比例函数经过点A和点B，．

(1)求反比例函数和直线AB的解析式；
(2)点为y轴上一动点，且∠AQB为钝角，求点Q的纵坐标t的取值范围；
(3)点D在直线AB上且在第二象限反比例函数图像的上方运动，过点D作x轴、y轴的垂线分别交反比例函数的图像于点F、E，直线EF分别交x轴、y轴于点N、M，设点D的横坐标为s，求的值．




16．如图，已知一次函数与反比例函数的图象相交于，两点，过点作轴于点，连接．

(1)求，的值和点坐标；
(2)将沿轴向右平移，对应得到，当反比例函数图象经过的中点时，求的面积；
(3)在第一象限内的双曲线上求一点，使得．

17．如图1，一次函数y=kx-3（k≠0）的图象与y轴交于点B，与反比例函数y=（x＞0）的图象交于点A（8，1）．

(1)求出一次函数与反比例函数的解析式；
(2)点C是线段AB上一点（不与A，B重合），过点C作y轴的平行线与该反比例函数的图象交于点D，连接OC，OD，AD，当tan∠ADC=2时，求点C的坐标；
(3)在（2）的前提下，将△OCD沿射线BA方向平移一定的距离后，得到△O'CD'，若点O的对应点O'恰好落在该反比例函数图象上（如图2），求出点O'，D'的坐标．






18．如图，一次函数的图象与x轴、y轴分别交于点A、点B，与反比例函数的图象交于点C、点D．

(1)直接写出点B的坐标；
(2)作轴于，作轴于．连接，求证：EF//CD；
(3)若点N在x轴上，且满足的N点有且只有一个，求k的值．

参考答案：
1．(1)；
(2)6
(3)或

【分析】（1）将点代入反比例函数解析式得出，根据，，待定系数法求解析式即可求解；
（2）根据一次函数得出，然后根据三角形面积公式进行计算即可求解；
（3）根据图象直接写出不等式的解集，即可求解．
【解析】（1）解：∵反比例函数的图象过点，
∴，即，
∴反比例函数的解析式为：．
∵一次函数的图象过点，
∴，
解得．
∴一次函数的解析式为：；
（2）∵由；
令，则，
∴，
即．
∴；
（3）∵，．
∴不等式的解集为：或．
【点评】本题考查了一次函数与反比例函数综合，待定系数法求解析式，数形结合是解题的关键．
2．(1)，图见解析
(2)或
(3)

【分析】（1）根据反比例函数求点A、B的坐标，再利用待定系数法求一次函数的表达式，最后求出一次函数图象与x轴和y轴的交点，即可作出图象；
（2）根据图象直接写出不等式的解集即可；
（3）根据对称求出点C的坐标，再利用点A、B、C的坐标求出的高和底，即可求出面积．
【解析】（1）解：∵点A、B在反比例函数的图象上，
∴分别把，代入，
解得：，，
所以，，
∵点A、B在一次函数图象上，
∴分别把，代入，
可得：，
解得，
∴一次函数的解析式是：，
一次函数的图象如图所示：

（2）解：，即一次函数的图象在反比例函数图象的下方，
∴由图象可知：或．
（3）解：∵点与点C关于x轴对称，
∴点，
如图所示：

，上的高是4，
∴的面积为：．
【点评】本题考查了用待定系数法求一次函数、反比例函数和一次函数交点的问题，熟练掌握反比例函数和一次函数的图象和性质、三角形面积公式是解题的关键．
3．(1)，
(2)或
(3)或

【分析】（1）把代入解得，即可得到反比例函数的解析式为，再把代入得，，得到，利用待定系数法求出一次函数解析式即可；
（2）设点的坐标为，设直线与y轴交于点,求出，则利用求得n的值，即可得到点P的坐标；
（3）根据图象的位置关系即可得到答案．
【解析】（1）解：把代入得，，
解得，
∴反比例函数的解析式为，
把代入得，，
∴，
把点和代入得，
，解得，
∴一次函数的解析式为；
（2）设点的坐标为，设直线与y轴交于点,

当时，，
∴直线与y轴交于点，
则，
则，
则，
解得或，
∴点P的坐标是或；
（3）由图象可知当或时，反比例函数图象在一次函数图象上方，
∴当或时，．
【点评】此题考查了反比例函数和一次函数综合题，用到了待定系数法、函数图象的交点等知识，数形结合和准确计算是解题的关键．
4．(1)
(2)或
(3)或

【分析】（1）点，在一次函数上，求出的值，待定系数法求出的表达式即可；
（2）找到直线在双曲线上方时，的取值范围即可；
（3）的面积等于的面积，得到点到直线的距离等于点到直线的距离，根据平行线间的距离处处相等，将直线向上或向下平移1个单位，得到直线，直线与双曲线在第一象限的交点即为点，进行求解即可．
【解析】（1）解：∵一次函数的图象与反比例函数的图象交于点，，
∴，
∴，
∴，，
∴，
∴；
（2）解：由图象可知：
当或时，直线在双曲线上方，
∴一次函数值大于反比例函数值时的取值范围为：或；
（3）解：∵的面积等于的面积，
∴点到直线的距离等于点到直线的距离，
∴将直线向上或向下平移1个单位，得到直线，直线与双曲线在第一象限的交点即为点，如图：

∵，
∴，，
联立，解得：或（不合题意，舍去）；
∴；
联立，解得：或（不合题意，舍去）；
∴；
综上：点的坐标为：或．
【点评】本题考查反比例函数与一次函数的综合应用．正确的求出函数解析式，利用数形结合的思想进行求解，是解题的关键．
5．(1)反比例函数的表达式为，一次函数表达式为．
(2)或
(3)

【分析】（1）由的面积为3，可求出a的值，确定反比例函数的关系式，把点坐标代入可求b的值．
（2）结合图像观察，求一次函数图像位于反比例函数图像的下方时，自变量x的取值范围即可．
（3）作对称点关于x的对称点，直线与x轴交点就是所求的点，求出直线与x轴的交点坐标即可．
【解析】（1）解：根据题意，，
，
，
结合图形，可得，
将代入得，
反比例函数的表达式为．
把代入反比例函数得，
，
将和代入解得：，，
一次函数表达式为．
（2）由图象可以看出的解集为或．
（3）解：如图，作点关于x轴的对称点，连接与x轴交于，此时最大．


，
，
设直线的关系式为，将，代入，
解得，，
直线的关系式为，
当时，解得，
．
【点评】本题考查反比例函数的图像和性质、一次函数、轴对称以及待定系数法求函数关系式等知识，理解轴对称知识作图是解题的关键．
6．(1)
(2)
(3)或或

【分析】（1）将点和代入一次函数求出a、b的值，得出点，，将点代入，求出m的值即可；
（2）作B点关于y轴的对称点，连接交y轴于点P，连接，当A、P、三点共线时，的周长最小，求出直线的解析式为，最后求出点P的坐标即可；
（3）设点D的坐标为，分三种情况进行讨论，为平行四边形的对角线，为平行四边形的边，且点A平移到点P，点B平移到点D，为平行四边形的边，且点A平移到点D，点B平移到点P，分别求出结果即可．
【解析】（1）解：将点和代入一次函数得：
，
解得：，
∴点，，
将点代入，解得，即．
（2）解：作B点关于y轴的对称点，连接交y轴于点P，连接，

∴，
∴，
当A、P、三点共线时，的周长最小，
∵，
∴，
设直线的解析式为，
∴，解得，
∴，
把代入得：，
∴；
（3）解：设点D的坐标为，
当为平行四边形的对角线时，如图所示：

∵平行四边形的对角线互相平分，
∴的中点也是的中点，
∴，
解得：，
∴此时点D的坐标为；
当为平行四边形的边，且点A平移到点P，点B平移到点D时，如图所示：

，
解得：，
∴此时点D的坐标为：；
当为平行四边形的边，且点A平移到点D，点B平移到点P时，如图所示：

，
解得：，
∴此时点D的坐标为：；
综上分析可知，点D的坐标为或或．
【点评】本题主要考查了反比例函数和一次函数的综合，求一次函数解析式，中点坐标公式，平行四边形的性质，解题的关键是作出辅助线，熟练掌握待定系数法，注意分类讨论．
7．(1)；
(2)；
(3)．

【分析】（1）时，当由题意可知，求得，由在，代入法求解即可；
（2）依题意得，由在上可得，由一次函数y的值随x值的增大而增大得即或，解不等式组即可；
（3）如图，可知在线段上，可得，，作轴于A，作轴于B，作轴于C，则，，则有，求得和即可求解．
【解析】（1）解：当时，由题意可知，
在上，
，
，
在，
则有，
解得：，
；
（2）依题意得：，
，
，
，
由一次函数y的值随x值的增大而增大，
，
即，
反比例函数的图象在第一象限，
，
，
即或，
或无解，
故答案为：；
（3）如图，，
在线段上，
，，
作轴于A，作轴于B，作轴于C，
则，，
，，
，
，
，
，
当时，
，
，
，
，
．

【点评】本题考查了一次函数和反比函数综合，一次函数图象和性质坐标与图形，代入法求解，相似三角形的判定和性质的应用；解题的关键是熟练掌握坐标与图形的关系．
8．(1)反比例函数的表达式为，一次函数的表达式为
(2)的取值范围为或
(3)点的坐标为或．

【分析】（1）把点坐标代入解方程得到反比例函数的表达式为，把点坐标代入求得，把点坐标，点坐标代入得解方程组得到一次函数的表达式为；
（2）根据一次函数及反比例函数的图象交于点，点，即可得到结论；
（3）分两种情况：①若在线段上，过点作平行于轴的直线，过点作垂直于直线于点，过点作垂直于直线于点．②当点在点的下方时，
过点作平行于轴的直线，过A点作垂直直线于点，过点作垂直的延长线于点．分别求解即可．
【解析】（1）解：把点坐标代入得，
，
，
反比例函数的表达式为，
把点坐标代入得，，
，
把点坐标，点坐标代入得，
，
解得，
一次函数的表达式为；
（2）解：∵一次函数及反比例函数的图象交于点，点，
∴当时，的取值范围为或；
（3）解：①若在线段上,
过点作平行于轴的直线，过点作垂直于直线于点，过点作垂直于直线于点．

设，
∵，
∴，
∴
∵
∴
∴
解得：

∴点的坐标为
②当点在点的下方时，
过点作平行于轴的直线，过点作垂直直线于点，过点作垂直的延长线于点．

设，
∵
∴
∴
∵
∴
∴
解得：

∴点的坐标为．
综上所述：点的坐标为或．
【点评】本题考查了反比例函数的综合题，待定系数法求函数的解析式，相似三角形的判定和性质，解不等式，正确的作出辅助线是解题的关键．
9．(1)一次函数的表达式为，反比例函数的解析式为
(2)
(3)存在，满足题意的点D的横坐标为或

【分析】（1）将点B坐标代入直线AC的解析式中求出，进而得出一次函数解析式，进而求出点A坐标，最后将点A坐标代入反比例函数解析式中，即可求出反比例函数解析式；
（2）设点，利用的面积为7，建立方程求解，即可得出答案；
（3）根据题意分两种情况①当点F在D下方时，过点D作轴于点E，这点F作于点N，②当点F在点D上方时，过点D作轴于点G，过点F作于点M，分别求解即可．
【解析】（1）∵点在直线上．
∴，
∴，
∴一次函数的解析式为；
∵点A在直线上，且点A的纵坐标为4，
∴，
∴，
∴．
∵点A在双曲线上，
∴．
∴反比例函数的解析式为；
（2）由（1）知，直线的解析式为，
设点，如图1，

∵，
∴，
∵的面积为7，
∴，
∴，
∴；
（3）需要分两种情况：
①当点F在D下方时．如图，过点D作轴于点E，这点F作于点N，
∴，
∵，
∴，
∴，
∴．
∴，
∵，
∴，
∴，
∵，∴，
设点D的横坐标为n，则，
∴，∴，
∴，
解得（负值舍去）．
即此时点D的坐标为：．
②当点F在点D上方时，如图，过点D作轴于点G，过点F作于点M，

∴，
∵，
∴，
∴，
∴，
∴，
∵，
∴，
∴，
∵．
∴，
设点D的横坐标为t，则，
∴，
∴．
∴．
解得（负值舍去）．
即此时点D的横坐标为：．
综上，满足题意的点D的横坐标为：或．
【点评】本题是反比例函数综合题，主要考查了待定系数法，三角形的面积公式，相似三角形的性质，正确理解题意是解题的关键．
10．(1)；
(2)
(3)或

【分析】（1）先把点A的坐标为代入反比例函数求得的值，再把点B的坐标为代入反比例函数的解析式求得，最后把A，B两点代入即可求解；
（2）利用一次函数的解析式求得点的坐标，利用即可求解；
（3）存在，分两种情况：①若时，如图所示，利用两点间的距离公式和勾股定理即可求解；②若时，如图所示，过点作轴，垂足为点，即可求解．
【解析】（1）解：∵点A的坐标为在反比例函数的图象上，
∴，
∴反比例函数的解析式为，
又∵点B的坐标为也在上，
∴，
∵A的坐标为，B的坐标为都在一次函数的图象上，
∴，解得，
∴一次函数的解析式为；
（2）解：∵直线与轴交于点，
∴，
∴，
∵A的坐标为，B的坐标为，
∴


（3）解：∵点在轴上，设点，则，
若时，如图所示，

∵点A的坐标为，
∴，，
∵是直角三角形，
∴，即，
解得，
∴点的坐标为
若时，如图所示，过点作轴，垂足为点，

∵点A的坐标为，
∴点的坐标为，
综上可得点的坐标为或．
【点评】此题是反比例函数综合题，主要考查了待定系数法，三角形的面积公式，直角三角形的性质，用分类讨论和方程思想解决问题是解本题的关键．
11．(1)，
(2)
(3)或

【分析】（1）利用点在上求，进而代入反比例函数求得，即可求得反比例函数的表达式；
（2）把代入反比例函数，求得，观察图象即可求得当时，不等式的解集；
（3）由直线求得，设出点坐标表示三角形面积，求出点坐标．
（1）
解：把点代入，得，
解得，
，
反比例函数的图象经过点，
，
反比例函数的表达式为；
（2）
解：把代入反比例函数得：，
，
由图象可知，当时，不等式的解集为：；
（3）
解：当时，则，
点，
设点的坐标为，
，
，
，
点或．


【点评】本题是一次函数和反比例函数交点问题，一次函数图象上点的坐标特征，待定系数法求反比例函数的解析式，三角形的面积以及函数与不等式的关系，解题的关键是利用数形结合思想求解．
12．(1)，
(2)9
(3)(-8，0)或(-5，0)或(5，0)或(，0)

【分析】（1）首先把，代入中，就可以确定m和 n的值，再把A、B两点的坐标代入，可以求得一次函数与反比例函数的表达式；
（2）分别过点A，B作AD⊥轴于点D，BE⊥轴于点E，设直线AB与轴交于点C，求出点C的坐标，求出OC、AD、BE的值，然后利用面积的分割法求出△AOB的面积；
（3）根据AO=OP，AP=AO，AP=OP三种情况，结合两点间的距离公式分类讨论，得出点的坐标．
【解析】（1）把A（-4，3）代入，得
  ∴
∴反比例函数的表达式为
把B（2，）代入，得，
∴B（2，-6），
把A（-4，3），B（2，-6）代入，得
，  解得
∴一次函数的表达式为；
（2）如图，分别过点A，B作AD⊥轴于点D，BE⊥轴于点E，
设直线AB与轴交于点C，
把代入，
得， 解得，
∴C（-2，0）
∴OC=2
∵A（-4，3），B（2，-6）
∴AD=3，BE=6
∴S△AOB=S△AOC+S△BOC=OC●AD+OC●BE=×2×3+×2×6=9
即△AOB的面积是9；

（3）设P（x，0）
∵A（-4，3）
∴，
当OP=OA时，
∵，
∴，
∴x=-5，或x=5，
当AP=AO时，
∵
∴，，
∴x=0（舍去），或x=-8，
当PA=PO时，，
∴8x+25=0，
∴
∴点P的坐标.为（-8，0）或（-5，0）或（5，0）或（，0）

【点评】本题主要考查了反比例函数与一次函数综合，解决问题的关键是熟练掌握一次函数性质和反比例函数性质，两点间的距离公式，等腰三角形的性质，分类讨论．
13．(1)（1，3）；（3，1）
(2)①0＜m＜1或m＞3；②若△POD的面积最小时，m的值为1或3

【分析】（1）将y1＝﹣x+4代入y2＝中可得出关于x的方程，解之即可得出x的值，再利用一次的数图象上点的坐标特征，即可求出点A，B的坐标；
（2）①观察函数图象，根据两函数图象的上下位置关系，可得出当y13；
②由原P的横坐标可得出点P的坐标，利用三角形的面积公式可得出S△POD关于m的函数关系式，再利用二次函数的性质即可解决最值问题．
（1）
解：（1）将y1＝﹣x+4代入y2＝得：-x+4=，
整理得：x2-4x+3=0，
解得：x1=1，x2=3，
经检验，x1=1，x2=3是原方程的解，且符合题意．
当x=1时，y1=-1+4=3，
∴点A的坐标为（1，3）；
当x=3时，y1=-3+4=1，
∴点B的坐标为（3，1）．
故答案为：（1，3）；（3，1）．
（2）
①观察两函数图象的上下位置关系，可知：
当03时，一次函数y1＝﹣x+4的图象在反比例函数y2＝的图象的下方，
∴当y13．
故答案为：0＜m＜1或m＞3．
②∵点P在线段AB上，
∴1≤m≤3，点P的坐标为（m，﹣m+4）．
∵PD⊥x轴于点D，
∴PD＝﹣m+4，OD＝m，
∴S△POD＝PD•OD＝（﹣m+4）•m＝﹣m2+2m＝﹣（m﹣2）2+2．
∵﹣＜0，
∴当1≤m≤2时，S△POD随m的增大而增大；
当2≤m≤3时，S△POD随m的增大而减小．
当m＝1时，S△POD＝﹣（1﹣2）2+2＝；
当m＝3时，S△POD＝﹣（3﹣2）2+2＝．
∵＝，
∴若△POD的面积最小时，则m的值为1或3．
【点评】本题考查了反比例函数的综合题、一次函数图象上点的坐标特征、反比例函数图象上点的坐标特征、三角形的面积以及二次函数的性质，解题的关键是：（1）将一次函数解析式代入反比例函数解析式中，通过解方程求出两点的横坐标；（2）①利用数形结合，解决问题；②利用三角形的面积计算公式，找出S△POD关于m的函数关系式．
14．(1)，；
(2)①8；②符合条件的点坐标是和．

【分析】（1）将点代入，求出，即可得，将点代入，即可求出k；
（2）①如图，过A作轴于点，过作轴于点，交于点，求出，，得到CE，进一步可求出△ABC的面积；②设，．分情况讨论：ⅰ、当四边形为平行四边形时，ⅱ、当四边形为平行四边形时，计算即可．
【解析】（1）解：将点代入，得，，
将点代入，得，
反比例函数的解析式为．
（2）解：①如图，过A作轴于点，过作轴于点，交于点，

∴，
∵，
∴，
∴，
∴，
∴，
∴，
∴，
∴．
②分两种情况：设，．
ⅰ、如图，当四边形为平行四边形时，

∵点向下平移1个单位、向右平移个单位得到点，
∴点向下平移1个单位，向右平移个单位得到点，
∴，，
∴．
ⅱ、如图，当四边形为平行四边形时，

∵点向上平移1个单位，向左平移个单位得到点，
∴点向上平移1个单位，向左平移个单位得到点，
∴，，
∴．
综上所述，符合条件的点坐标是和．
【点评】本题考查一次函数与反比例函数的综合，待定系数法求函数解析式，平行四边形的性质，解题的关键是掌握待定系数法求函数解析式，平行四边形的性质．
15．(1)，

(2)，且
(3)

【分析】（1）过A点作AP⊥x轴于点P，连接AO，在Rt△AOP中，利用sin∠AOC=，求出AO=5，再利用勾股定理求出OP，则可求出A点坐标，将A点坐标代入反比例函数解析式即可求出m的值，则反比例函数解析式即得，据此可求出B点坐标，结合A、B点坐标待定系数法即可求出直线AB的解析式；
（2）先求出直线AB与y轴的交点坐标，连接AQ、BQ，当AQ⊥BQ时，在Rt△ABQ中，利用勾股定理有，则可求出t的值，可知构成∠AQB为钝角时，t的取值范围；
（3）结合（1）所求的直线AB的解析式以及反比例函数解析式，根据D点的横坐标，求出D点的纵坐标，则有F点的横坐标为s，E点的纵坐标为：，则可求出F、E点的坐标，用待定系数法即可求出直线EF的解析式，则其与坐标轴的交点可求，即OM、ON可求，则问题得解．
（1）
过A点作AP⊥x轴于点P，连接AO，如图，

∵A点坐标为(a,3)，
∴AP=3，
在Rt△AOP中，sin∠AOC=，
∴AO=5，
∴根据勾股定理有：，
∴a=-4，即A点坐标为(-4,3)，
∵A点在上，
∴，则有，
则反比例函数解析式为：，
∵B点(b,-6)在上，
∴，即B点坐标为(2,-6)，
∵A点、B点在直线，
∴有：，解得，
即直线AB的解析式为：；
（2）
连接AQ、BQ，如图，

令x=0，可得y=-3，
则直线AB与y轴的交点坐标为(0,-3)，
当AQ⊥BQ时，在Rt△ABQ中，利用勾股定理有，
∵A点坐标为(-4,3)，B点坐标为(2,-6)，Q点坐标(0,t)，
∴，，，
∴，化简得：，
解得，，
当t=-3时，A、Q、B三点共线，故∠AQB无法为钝角
∴，
∴可知当，且时，构成的∠AQB为钝角；
（3）
∵D点在直线AB上，且横坐标为s，且D点在第二象限的反比例函数图像上方，
∴即D点在A点上方，
∴令x=s，得，则D点坐标为，且s＜-4，
∵DG⊥x轴，DH⊥y轴，
∴F点的横坐标为s，E点的纵坐标为：，
∵F点在反比例函数上，
∴令x=s，得，则F点的坐标为：，
∵E点在反比例函数上，
∴令y=，得，解得，
则E点的坐标为：，
设直线EF的解析式为：，
∴代入E、F坐标有：，
解得：，
∴直线EF的解析式为：，
∴当x=0时，，
即M点坐标为：，
∴，
当y=0时，得，解得，
即N点坐标为：，
∴，
∴．
【点评】本题是一次函数和反比例函数的综合题，考查了求解一次函数和反比例函数的解析式、三角函数、勾股定理以及根据求解函数与坐标轴的交点坐标等知识，利用构造直角三角形来确定形成钝角∠AQB的临界条件是解答本题的关键．
16．(1)，，
(2)
(3)

【分析】（1）将A点坐标代入一次函数和反比例函数解析式，求出两个解析式后，再联立起来，即可解出B点坐标；
（2）先在AC上取中点坐标N，得到M、N点的纵坐标是一样的，可算出M点坐标，再利用的面积计算求出的面积；
（3）过点作轴的垂线，交轴于点，可知，然后在直线上方找一点，使得，关于对称，即满足，设，就得到，这样点坐标就出来了，然后算出直线的解析式，与反比例函数联立就可算出点P的坐标；
（1）
将代入一次函数表达式与反比例函数表达式，
得，．
由
解得，或，
点坐标为；
（2）
如图1，取中点，则点的坐标为，连接，
设点坐标为，代入，得，
，
；

（3）
如图2，过点作轴的垂线，交轴于点．易知，
∴在直线上方找一点，使得，关于对称，即满足，
设点，，，
则有解得，
，
∴直线的函数表达式为，
联立解得
或（舍去），
故点的坐标为．
【点评】本题考查一次函数与反比例函数的综合，三角函数值的应用；熟练掌握一次函数与反比例函数的图像与性质，三角函数值的应用是解决本题的关键．
17．(1)一次函数解析式为y=x-3，反比例函数解析式为y=；
(2)点C的坐标为（2，-2）；
(3)O'（4，2），D'（6，6）．

【分析】（1）把A坐标代入一次函数解析式求出k的值，确定出一次函数解析式，再将A坐标代入反比例函数解析式求出k的值，即可确定出反比例解析式；（2）设点C（a，a-3）（0＜a＜8），则有D（a，），过A作AE⊥CD于点E，用a表示出DE、AE的长，再由正切函数得到方程，解方程求解即可；
（3）连接OO'，由平移可得：OO'∥AC，根据两直线平行时k的值相同确定出直线OO'的解析式，与反比例函数解析式联立求出交点O'的坐标，根据平移的性质，由O平移到O'的路径确定出D平移到D'的路径，进而确定出D'的坐标即可．
（1）
解：∵点A（8，1）在直线y=kx-3上，
∴1=8k-3，
解得：k=，
∴一次函数解析式为y=x-3，
∵A（8，1）在y=（x＞0）的图象上，
∴1=，
解得：m=8，
则反比例函数解析式为y=；
（2）
解：设C（a，a-3）（0＜a＜8），则有D（a，），
过A作AE⊥CD于点E，

则AE=8-a，DE=-1，
∵tan∠ADC=2，即AE=2DE，
∴8-a=2(-1)，
整理得：a2-10a+16=0，
解得：a=8(舍去)或a=2，
∴点C的坐标为（2，-2）；
（3）
解：连接OO'，由平移可得：OO'∥AC，

∴直线OO'的解析式为y=x，
联立得：，
解得：或（不合题意，舍去），
∴O'（4，2），
即O（0，0）通过往右平移4个单位，往上平移2个单位得到O'（4，2），
又由（2）中知D坐标为（2，4），
∴点D（2，4）往右平移4个单位，往上平移2个单位得到D'（6，6）．
【点评】此题属于反比例函数与一次函数综合题，涉及的知识有：待定系数法求一次函数及反比例函数解析式，一次函数与反比例函数的交点，平移的性质，熟练掌握各自的性质是解本题的关键．
18．(1)（4，0）
(2)见解析
(3)k的值为-1

【分析】（1）一次函数，令y=0，解方程可得x的值，可得点B的坐标；
（2）设点C、点D的横坐标分别为m，n，联立一次函数与反比例函数，可得m+n=4，由题意可得点A的坐标为（0，-4k），可得，进而可证EF//CD；
（3）过点C、D分别作CP、DQ垂直于x轴，易得△CNP∽△NDQ，可得，设N（x，0），代入可得关于x的一元二次方程，因为存在唯一的点N，所以方程有两个相等的实数根，可得k的值．
（1）
解：点B的坐标为（4，0）
点B为一次函数与x轴的交点，当y=0时，kx-4k=0，x=4，
∴点B的坐标为（4，0）．
（2）
证明：一次函数的图象与反比例函数的图象交于点C、点D两点，
∴ ，
∴ ，
设点C、点D的横坐标分别为m，n，
则m+n=4 ，
如图，由点C是一次函数的图象与反比例函数的图象的交点，
∴点C的纵坐标为，
代入一次函数解析式得：，则 ，
由题意可得，点A的坐标为（0，-4k），
∴ ，
又m+n=4，
∴m-4=-n，
∴，
又 ，
∴EF//CD．

（3）
解：一次函数的图象与反比例函数的图象交于点C、点D两点，
∴ ，
∴ ，
设点C、点D的横坐标分别为m，n
则m+n=4， ，
如图，过点C、D分别作CP、DQ垂直于x轴，

当时，∠CNP+∠DNQ=90°，
又∠CNP+∠NCP=90°，
∴∠NCP=∠DNQ，
∴△CNP∽△NDQ，
∴，
设N（x，0），
则 ，
∴ ，
即，
当△=时，
即k=-1时，满足的N点有且只有一个
即k的值为-1．
【点评】本题是反比例函数综合题，主要考查了反比例函数与一次函数图象的交点问题，一元二次方程根与系数的关系，根的判别式，比例线段等，综合分析问题，灵活运用所学知识是解题的关键．