专题11 立体几何的综合问题-2022-2023学年高一数学下学期期中期末必考题型归纳及过关测试（人教A版2019）

这是一份专题11 立体几何的综合问题-2022-2023学年高一数学下学期期中期末必考题型归纳及过关测试（人教A版2019），文件包含专题11立体几何的综合问题解析版docx、专题11立体几何的综合问题原卷版docx等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。
专题11 立体几何的综合问题
【典型例题】
例1．（2023·全国·高一专题练习）如图，在矩形中，，E为的中点，将沿翻折到的位置，其中平面，M为的中点，则在翻折过程中，有如下下列结论：
①恒有平面；②B与M两点间距离恒为定值；③三棱锥体积最大值为；
④存在某个位置，使得平面平面.
其中正确的结论个数是（    ）.

A．1 B．2 C．3 D．4
【答案】C
【解析】

对于①：如图，取的中点，连接.则且.
又且，所以且，
所以四边形是平行四边形，所以.
又平面，平面，
所以平面.故①正确;
对于②：因为，
根据余弦定理，得，解得.
因为，所以.故②正确;
对于③：连接.因为为的中点，
所以三棱锥的体积是三棱锥的体积的两倍.
设为到底面的距离，则三棱锥的体积，
.
当平面⊥平面时，h达到最大值，所以取到最大值.
此时，，

所以
所以三棱锥的体积的最大值为.故③正确；
对于④：假设平面⊥平面，又平面∩平面=，，
所以⊥平面，所以，
则在△中，∠ =90°，，所以.
又所以故三点共线，
所以，所以平面，与题干条件平面矛盾，故④不正确.
故选：C.
例2．（2023春·全国·高一专题练习）在九章算术商功中将正四面形棱台体棱台的上、下底面均为正方形称为方亭在方亭中，，方亭的体积为，则侧面的面积为（    ）
A． B． C． D．
【答案】A
【解析】设方亭的高为，因为，方亭的体积为，
所以，解得，
如图，

过作，垂足为，
连接，，过作，垂足为，易知四边形为等腰梯形，
且，，则，
，
因为侧面为等腰梯形，
所以，
所以侧面的面积为．
故选: A．
例3．（多选题）（2023·全国·高一专题练习）如图，在长方体中，，，E为棱的中点，则（    ）

A．面 B．
C．平面截该长方体所得截面面积为 D．三棱锥的体积为
【答案】ABD
【解析】对于选项A：连接，

为长方体，，，∴四边形是平行四边形，
，
平面，平面，
面，故选项A正确；
对于选项B：
，
，
平面，
在平面上的投影为，
，故选项B正确；
对于选项C：
根据长方体对称性易知平面截该长方体所得截面面积为，
，，
，，，
，
由，可得，
则，故C错误；
对于选项D：
三棱锥的底面积，高为，
则三棱锥的体积为，故D正确；
故选：ABD.
例4．（多选题）（2023春·全国·高一专题练习）在底面边长为2、高为4的正四棱柱中，为棱上一点，且分别为线段上的动点，为底面的中心，为线段的中点，则下列命题正确的是（    ）

A．与共面
B．三棱锥的体积为
C．的最小值为
D．当时，过三点的平面截正四棱柱所得截面的周长为
【答案】ACD
【解析】对于A，如图1，在中，因为为的中点，所以，所以与共面，所以A正确；
对于B，由，因为到平面的距离为定值2，且的面积为1，所以三棱锥的体积为，所以B错误；

对于C，如图2，展开平面，使点共面，过作，交与
点，交与点，则此时最小，易求的最小值为，则C正确；

对于D，如图3，取，连接，则，又，所以，所以共面，即过三点的正四棱柱的截面为，由，则是等腰梯形，且，所以平面截正四棱柱所得截面的周长为，所以D正确.

故选:ACD.
例5．（2023春·全国·高一专题练习）已知正三棱柱的所有棱长为，以为球心，为半径的球面与侧面的交线长为__________．
【答案】
【解析】设的中点为，易知，又因为面面，且面面，所以面，所以题中所求交线即为以为圆心，为半径的一段圆弧．设该圆弧与的交点分别为，球与侧面的交线如图所示，则，
易知，

所以该圆弧所对的圆心角为，
故所求弧长为，
故答案为：.
例6．（2023春·全国·高一专题练习）一名学生参加学校社团活动，利用3D技术打印一个几何模型该模型由一个几何体及其外接球组成，几何体由一个内角都是120°的六边形绕边旋转一周得到且满足，，则球与几何体的体积之比为______.
【答案】
【解析】方法一：设，，连接，
因为，且每一个内角都为，
所以，
所以，
即，所以四边形是长方形，
，
∴，
∴，，
，
；

方法二：设，，

∴，旋转形成的几何体为一个圆台挖去一个圆锥，

，
，∴，
∵几何体存在外接球，设中点为，∴为球心，
由，
∴，，∴，
，
∴.
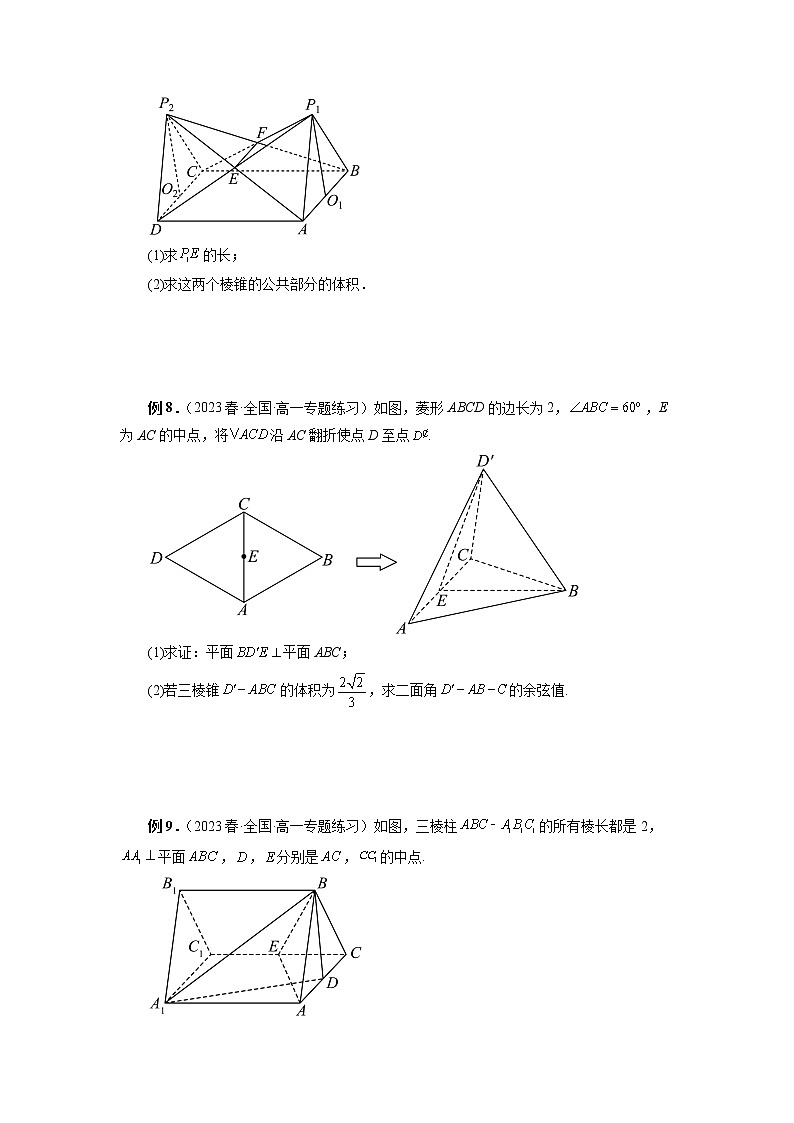
例7．（2023春·全国·高一专题练习）已知两个四棱锥与的公共底面是边长为2的正方形，顶点、在底面的同侧，棱锥的高，、分别为AB、CD的中点，与交于点E，与交于点F．

(1)求的长；
(2)求这两个棱锥的公共部分的体积．
【解析】（1）连接，如图所示：

因为平面，平面，所以，又，
所以四边形是矩形，所以，且，
又分别为的中点，所以，且，
所以，且，所以四边形为平行四边形，
又对角线，所以为的中点，
由题意可知：在中，，
所以.
（2）连接，交于点，过点作于，

由题意知，故，又，，
平面，所以平面，
因为平面，故，又，平面，
所以平面，即是四棱锥的高，
由（1）同理可得点为线段的中点，所以，且，
在中，，则，
所以，
因为，
所以.
例8．（2023春·全国·高一专题练习）如图，菱形ABCD的边长为2，，E为AC的中点，将沿AC翻折使点D至点.

(1)求证：平面平面ABC；
(2)若三棱锥的体积为，求二面角的余弦值.
【解析】（1）证明：在菱形中，，∴和均为等边三角形，
又∵E为AC的中点，∴，，，平面，∴平面，
又∵平面ABC，∴平面平面ABC.
（2）过作于点，∵平面平面ABC，平面，∴平面ABC.
∴.
过M作于点，连接，
∵平面ABC，∴，∵平面，∴平面，
∵平面，∴.
∴即为二面角的平面角，

，∴，，
∴，∴.
故二面角的余弦值为.
例9．（2023春·全国·高一专题练习）如图，三棱柱的所有棱长都是2，平面，，分别是，的中点.

(1)求证：平面平面；
(2)求平面和平面夹角的余弦值；
(3)在线段（含端点）上是否存在点，使点到平面的距离为？若存在，请指出点的位置，并证明你的结论；若不存在，请说明理由.
【解析】（1）证明：因为平面，平面，
所以，
又为边长为2的正三角形，为中点，
所以，

所以平面，
平面，
所以①,
又，
所以，
所以，
所以，
所以(为与的交点)，
所以②，
又因为③,
由①②③可得平面，
又因为平面，
所以平面平面；
（2）设,过作于，连接,

因为平面，
平面，
所以，
又因为，
，
则平面,
平面,
所以，
所以为平面和平面夹角，
在中，,
在中，，
所以，
所以中，,
所以；
（3）当点与点重合时，点到平面的距离为，
取中点，连接,

则∥，
所以四点共面，
又平面，
平面，
所以，
又，
,
所以平面，
设点到平面的距离为，
又,
即,
即,
所以，
解得.
故在线段存在点（端点处），使点到平面的距离为.
例10．（2023春·全国·高一专题练习）如图，在三棱锥中，平面平面，，，、分别为棱、的中点.

(1)求证：直线平面；
(2)若直线与平面所成的角为45°，直线与平面所成角为30°，求二面角的大小.
【解析】（1）证明：因为、分别为棱、的中点.
所以，在中，，
因为平面，平面，
所以，直线平面
（2）因为平面平面，平面平面，平面,
所以平面，
所以，是直线与平面所成的角，
因为直线与平面所成的角为45°，
所以，，
所以
因为平面，平面，
所以，，
因为，，平面，
所以平面，
所以，是直线与平面所成角，
因为直线与平面所成角为30°，
所以，
所以，
不妨设，则，
所以，为等腰直角三角形，
因为，，
所以是二面角的平面角，
所以二面角的大小为
例11．（2023春·全国·高一专题练习）如图，在三棱柱中，平面平面，侧面是边长为2的正方形，分别为的中点.

(1)证明：面
(2)请再从下列三个条件中选择一个补充在题干中，完成题目所给的问题.
①直线与平面所成角的大小为；②三棱锥的体积为；③. 若选择条件___________.
求（i）求二面角的余弦值；
（ii）求直线与平面的距离.
【解析】（1）证明：取中点G，连接FG、CG，∵分别为的中点，∴在三棱柱中，，且，∴四边形FECG为平行四边形，∴.
∵面，面，∴面；
（2）平面平面，平面平面=，又侧面是边长为2的正方形，则，∴面，面，∵面，∴.
取中点I，作于J，连接FI，IE，FJ，则平面，，∵平面，∴，
∵平面FIJ，∴平面FIJ，∵平面FIJ，∴，∴为二面角的平面角的补角.
∵面，∴直线与平面的距离即为E到平面的距离， 作于，由平面平面，平面平面=，则EK即为E到平面的距离，即直线与平面的距离.
选①，∵面，∴为直线与平面所成角，即，∴.
（i）在正中，易得，故在中，，故二面角的余弦值为；
（ii） 在正中，，故直线与平面的距离为；
选②，，为的中点，∴，∵面，∴，即，又，∴，∴，解得，∴，.
（i）在中，，故在中，，故二面角的余弦值为；
（ii）在中，，故直线与平面的距离为1；
选③， 取AB中点H，，连接OH，则O为中点，则且，由，∴，则，又，∴，∴，.
此时条件③与条件②一致，故（i）二面角的余弦值为；（ii）直线与平面的距离为1.

【过关测试】
一、单选题
1．（2023春·河北邯郸·高一校考阶段练习）一平面四边形OABC的直观图O′A′B′C′如图所示，其中O′C′⊥x′轴，A′B′⊥x′轴，B′C′∥y′轴，则四边形OABC的面积为（　　）

A． B．3 C．3 D．
【答案】B
【解析】设轴与交点为D，因O′C′⊥x′轴，A′B′⊥x′轴，则，又B′C′∥y′轴，则四边形为平行四边形，故.又，结合A′B′⊥x′轴，则，故.
则四边形面积为，因四边形面积是四边形OABC的面积的倍，则四边形OABC的面积为.
故选：B

2．（2023·全国·高一专题练习）在长方体中，若分别为的中点，过点作长方体的一截面，则该截面的周长为（    ）
A． B． C． D．
【答案】D
【解析】

连接，过点做交于点，连接，即可得到截面，
因为为中点，，所以，
因为，则，且，
，
所以截面的周长为
故选:D
3．（2023·全国·高一专题练习）如图，圆锥的底面半径为1，侧面展开图是一个圆心角为的扇形.把该圆锥截成圆台，已知圆台的下底面与该圆锥的底面重合，圆台的上底面半径为，则圆台的侧面积为（    ）

A． B． C． D．
【答案】C
【解析】假设圆锥半径，母线为，则.设圆台上底面为，母线为，则.
由已知可得，，所以.
如图，作出圆锥、圆台的轴截面

则有，所以.
所以圆台的侧面积为.
故选：C.
4．（2023·全国·高一专题练习）在数学探究活动课中，小华进行了如下探究：如图1，水平放置的正方体容器中注入了一定量的水；现将该正方体容器其中一个顶点固定在地面上，使得DA，DB，DC三条棱与水平面所成角均相等，此时水平面为HJK，如图2所示．若在图2中，则在图1中（    ）

A． B． C． D．
【答案】B
【解析】当DA，DB，DC三条棱与水平面所成角均相等时，三棱锥为正三棱锥，设正方体的棱长为3，
则，
所以，则题图1中，
则，所以.
故选：B
5．（2023·全国·高一专题练习）已知A，B，C，D在球O的表面上， 为等边三角形且边长为3，平面ABC，，则球O的表面积为（    ）
A． B． C． D．
【答案】C
【解析】球心在平面的投影为的中心，设为，连接，
是中点，连接，如图所示：

，，则，四边形为矩形，
，，故，.
故选：C
6．（2023·全国·高一专题练习）甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为，侧面积分别为和，体积分别为和．若，则（    ）
A． B． C． D．
【答案】A
【解析】设母线长为，甲圆锥底面半径为，乙圆锥底面圆半径为，
则，所以，
又，则，所以，
所以甲圆锥的高，
乙圆锥的高，
所以.
故选：A.
7．（2023·全国·高一专题练习）我国古代数学名著《九章算术》中“开立圆术”日：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径．意思是：球的体积V乘16，除以9，再开立方，即为球的直径d，由此我们可以推测当时球的表面积S计算公式为（    ）
A． B．
C． D．
【答案】A
【解析】因为，所以，所以，
所以，
故选：.
8．（2023·全国·高一专题练习）等于90°的二面角内有一点，过有于点，于，如果，则到的距离为（    ）
A． B． C． D．
【答案】C
【解析】

由，，，，则，，
且，面，故面，
面，连接，面，故，
所以到的距离为线段的长度，二面角为90°，故，
且，故.
故选：C
二、多选题
9．（2023春·浙江宁波·高一余姚中学校考阶段练习）某班级到一工厂参加社会实践劳动，加工出如图所示的圆台，在轴截面中，，且，下列说法正确的有（    ）

A．该圆台轴截面面积为
B．该圆台的体积为
C．该圆台的侧面积为
D．沿着该圆台表面，从点到中点的最短距离为
【答案】ACD
【解析】对于，由，且，
可得，高，
则圆台轴截面的面积为，故A正确；
对于B，圆台的体积为，故B错误；
对于C，圆台的体积为，故C正确；
对于，由圆台补成圆锥，可得大圆锥的母线长为，底面半径为，侧面展开图的圆心角．
设的中点为，连接，可得，
则．
所以沿着该圆台表面，从点到中点的最短距离为，故正确．

故选：ACD．
10．（2023春·河北邯郸·高一校考阶段练习）长方体中，，，，则（    ）
A．到平面的距离为
B．到平面的距离为
C．沿长方体的表面从到的最短距离为
D．沿长方体的表面从到的最短距离为
【答案】AC
【解析】如图，连接，因为，，，
所以，，，
在中，由余弦定理可得：，
所以，
则，
又，
设点到平面的距离为，由体积相等可得：
，即，
所以，解得：，故选项正确；选项错误；

长方体的表面可能有三种不同的方法展开，如图所示：

，，，
表面展开后，依第一个图形展开，则；
依第二个图形展开，则；
依第三个图形展开，则；
三者比较得：点沿长方形表面到的最短距离为，故选项正确，选项错误，
故选：.
11．（2023·全国·高一专题练习）已知正方体，过对角线作平面交棱于点，交棱于点，则：
①平面分正方体所得两部分的体积相等；
②四边形一定是平行四边形；
③平面与平面不可能垂直；
④四边形的面积有最大值.
其中所有正确结论的序号为（    ）
A．① B．② C．③ D．④
【答案】ABD
【解析】如图：

①由正方体的对称性可知，平面分正方体所得两部分的体积相等，①正确；
②因为平面 平面，平面平面，平面，所以,
因为平面 平面，平面平面，平面平面，所以，
所以四边形是平行四边形，②正确；
③在正方体中，有，，

又，平面，所以平面，
当分别为棱的中点时，有，则平面，
又平面，所以平面平面，③错误；
④设，正方体棱长为，，
则，，，
在中，由余弦定理可得，
所以，
由②得四边形一定是平行四边形，
所以，
所以当或时，取得最大值，④正确；
综上①②④正确，
故选：ABD
12．（2023春·全国·高一专题练习）如图，在边长为的正方体中，点在底面正方形内运动，则下列结论正确的是（    ）

A．若平面，则三棱锥的体积为定值
B．若平面，则动点的轨迹长度为
C．若，则动点的轨迹长度为
D．存在点，使得平面
【答案】AB
【解析】对于A，，，平面，平面，
平面，平面，又，平面，
平面平面，
则当平面时，点到平面的距离即为平面与平面之间的距离；
由正方体性质知：平面与平面之间距离，，
，
即三棱锥的体积为定值，A正确；
对于B，由A知：平面平面，
若平面，则平面，
又平面，平面平面，
点的轨迹为线段，则其轨迹长为，B正确；
对于C，若，则在以为球心，为半径的球面上，
则点轨迹是该球面与底面的交线，即点轨迹是以为圆心，为半径的四分之一圆，
点轨迹长为，C错误；
对于D，由正方体性质知：平面，
若存在点，使得平面，则，
平面，若平面，则，此时不成立；
若平面，平面，与为异面直线；
综上所述：不成立，即不存在点，使得平面，D错误.
故选：AB.
三、填空题
13．（2023·全国·高一专题练习）如图所示，△ABC和△A′B′C′的对应顶点的连线AA′，BB′，CC′交于同一点O，且＝＝＝，则＝________.

【答案】
【解析】∵，且，
∴，同理，.
因为平面，平面，所以平面，
同理可得：平面，又因为，且平面，
所以平面平面，
∵，，∴，
同理，
∴且，
∴，
故答案为：.
14．（2023·全国·高一专题练习）在正四棱柱中，E是BC的中点，F是的中点，P是棱所在直线上的动点．则下列四个命题：
①
②平面
③
④不存在过P的直线与正四棱柱的各个面都成等角．
其中正确命题的序号是______（写出所有正确命题的序号）．

【答案】①②③
【解析】在①中：∵正四棱柱中，E是BC的中点，F是的中点，P是棱所在直线上的动点，∴平面ECC1，又PE⊂平面，∴，故①正确；
在②中：

连接，则由E是BC的中点，F是的中点知，，
因为平面，平面，
所以平面，故②正确；
在③中：＝，＝，所以，故③正确；
在④中：由正方体性质知，过一个顶点的体对角线与正方体的各个面所成角都相等，故过点P做一条与以ABCD为底面的正方体的体对角线平行的直线，则该直线与正四棱柱的各个面都成等角．故④不正确；
故正确命题的序号为：①②③
故答案为：①②③
15．（2023·全国·高一专题练习）直三棱柱的所有棱长均为2，以为球心，为半径的球面与侧面的交线长为______．
【答案】
【解析】设的中点为，则，，
又因为面面，且面面面，
所以面，
所以题中所求交线即为以为圆心，为半径的一段圆弧，
设该圆弧与的交点分别为，
球与侧面的交线如图所示，则，
易知，

所以该圆弧所对的圆心角为，
故所求弧长为.
故答案为：.
16．（2023·全国·高一专题练习）从一个底面半径和高均为R的圆柱中，挖去一个以圆柱上底面为底，下底面中心为顶点的棱锥，得到一个如图几何体.如果用一个与圆柱下底面距离为d的平行平面去截这个几何体，截面面积为______.

【答案】
【解析】如图所示作出轴截面，
圆柱被平行于下底面的平面所截得的截面圆的半径，
设圆锥的截面圆的半径为，
因为，所以是等腰直角三角形.
又，所以，故，
所以截面积.
故答案为：.

四、解答题
17．（2023春·河北邯郸·高一校考阶段练习）如图所示，底面半径为1，高为1的圆柱中有一内接长方体，设矩形的面积为S，长方体的体积为V，，

(1)将S表示为x的函数；
(2)求V的最大值．
【解析】（1）连接，因为矩形ABCD内接于⊙O，
所以AC为⊙O的直径．
因为，，
所以，
所以，

（2）因为长方体的高，
所以，
因为，所以，
故当即时，V取得最大值，此时.
18．（2023·全国·高一专题练习）如图，在四棱锥中，底面为边长为2的菱形且对角线与交于点，底面，点是的中点.

(1)求证：；
(2)若三棱锥的体积为1，求的长.
【解析】（1）为菱形，
.
平面平面，
.
，平面,平面
平面.
平面，.
（2）点是的中点，，.
，
又，

.

19．（2023春·福建三明·高一三明一中校考阶段练习）如图，四边形ABCD是圆柱底面的内接四边形，PA是圆柱的母线，，，，C是上的一个动点.

(1)求圆柱的表面积；
(2)求四棱锥的体积的最大值.
【解析】（1）

连接BD，在中，，，，
由余弦定理，得
，
所以，设圆柱底面半径为r，
由正弦定理，得，
所以，故圆柱的表面积.
（2）由（1）知，中，，，
由余弦定理，得

，
即，当且仅当时，等号成立，
所以，
因为，，
所以四棱锥的体积，
，
故四棱锥的体积的最大值为.
20．（2023·全国·高一专题练习）如图，正四棱柱'．

(1)请在正四棱柱中，画出经过P、Q、R三点的截面（无需证明）；
(2)若Q、R分别为'中点，证明：AQ、CR、三线共点．
【解析】（1）作直线分别交的延长线于，连接交于，
连接交于点，连接，
如图五边形PSQRT即为所求；

（2）证明：如图，连接，，，则，，

∵Q、R分别为中点，
∴QR，又AC，
∴QR，而AC＝2QR，可得四边形AQRC为梯形，
设，则，
∵AQ⊂平面，∴O∈平面A′AB，同理O∈平面C′CB，
又平面平面，∴，
即AQ、CR、三线共点．
21．（2023·全国·高一专题练习）如图，正方体的棱长为4cm，分别是和的中点．

(1)画出过点的平面与平面及平面的两条交线；
(2)设过的平面与交于点P，求PM+PN的值．
【解析】（1）如图所示，连接并延长交的延长线于点，连接交于点，交延长线于点，连接交于点，连接，则即为所求作的截面．

如图示：平面与平面的交线为，平面与平面的交线为.
（2）由N为的中点，易得，所以，
因为，所以，得，
所以，，，
所以，．
所以．
22．（2023春·全国·高一专题练习）对于精美的礼物，通常人们会用包装纸把礼物包好，还会用彩带捆扎包装好的礼物，有时还会扎出一个花结.这些包装彩带也不便宜，因此在捆扎时不仅要考虑美观､结实，也要考虑尽量地节省包装彩带.以长方体的礼物为例，较为典型的两种捆扎方式分别为“十字”和“对角”，如下图所示.
“十字”捆扎
“对角”捆扎


假设1：将礼物视作一个长方体，其长为4，宽为2､高为1；假设2：不考虑花结处的彩带，将每一段彩带视为线段，且完全位于礼物的表面上；假设3：“十字”捆扎中，长方体表面上的每一段彩带（上底面和下底面各2段，每个侧面各1段）都与其相交的棱垂直；假设4：“对角”捆扎中，以某种方式展开长方体后，长方体表面上的每一段彩带（上底面和下底面各2段，每个侧面各1段）在其表面展开图上均落在同一条直线上.
(1)求“十字”捆扎中彩带的总长度；
(2)根据假设4绘制示意图，求“对角”捆扎中彩带的总长度，并比较两种捆扎方式，给出用彩带捆扎礼物的建议.
【解析】（1）采用“十字”捆扎中彩带的总长度为；
（2）

由于，因此在实际生活中包装彩带时应选择“对角”捆扎的方式，更节省包装彩带.
23．（2023春·全国·高一专题练习）在三棱柱中，，，，点为棱的中点，点是线段上的一动点，.

(1)求证：；
(2)求平面与平面所成的二面角的正弦值.
【解析】（1）由题意可知，，又，所以，
连接，如下图所示：

由，可知，是正三角形，
又点为棱的中点，所以，
平面，平面，，
所以平面，平面
所以.
（2）由（1）知，，
根据二面角定义可知，即为所求二面角的平面角或其补角，
在正三角形中，，所以，
因为，，所以，
又，且，所以平面，
而平面，所以，
在中，，
所以，
于是平面与平面所成的二面角的正弦值为