第7章 平面图形的认识（二）【专项练习】——2022-2023学年苏科版数学七年级下册单元综合复习（原卷版+解析版）

这是一份第7章 平面图形的认识（二）【专项练习】——2022-2023学年苏科版数学七年级下册单元综合复习（原卷版+解析版），文件包含第7章平面图形的认识二专项练习解析版docx、第7章平面图形的认识二专项练习原卷版docx等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。

第7章 平面图形的认识（二）

1．如图，在下列条件中，不能判定的是（    ）

A． B．
C． D．
【答案】D
【解析】解：A、因为，所以（同位角相等，两直线平行），故A选项不符合题意．
B、因为，所以（同旁内角互补，两直线平行），故B选项不符合题意．
C、因为，所以（内错角相等，两直线平行），故C选项不符合题意．
D、因为，所以（同位角相等，两直线平行），不能得出，故D选项符合题意．故选：D．
2．如图，下列说法错误的是（    ）．

A．与是同旁内角 B．与是内错角
C．与是内错角 D．与是同位角
【答案】D
【解析】解；A、与是同旁内角，故此选项不符合题意； B、与是内错角，故此选项不符合题意； C、与是内错角，故此选项不符合题意； D、与是同旁内角，故此选项符合题意；
故选：D．
3．直线、、中，，，则直线与直线的关系是（    ）．
A．相交 B．平行 C．垂直 D．不能确定
【答案】C
【解析】解：如图，

∵，
∴，
∵，
∴，
∴．
故选：C．
4．如图，平分，，若，则的度数是（    ）．

A．32° B．64° C．58° D．68°
【答案】B
【解析】解；∵，，
∴，
∵平分，
∴，
∵，
∴，
故选B．
5．如图，，，平分，则的大小为（　　）

A． B． C． D．
【答案】D
【解析】解：，
，
，
平分，
，
，
故选：D．
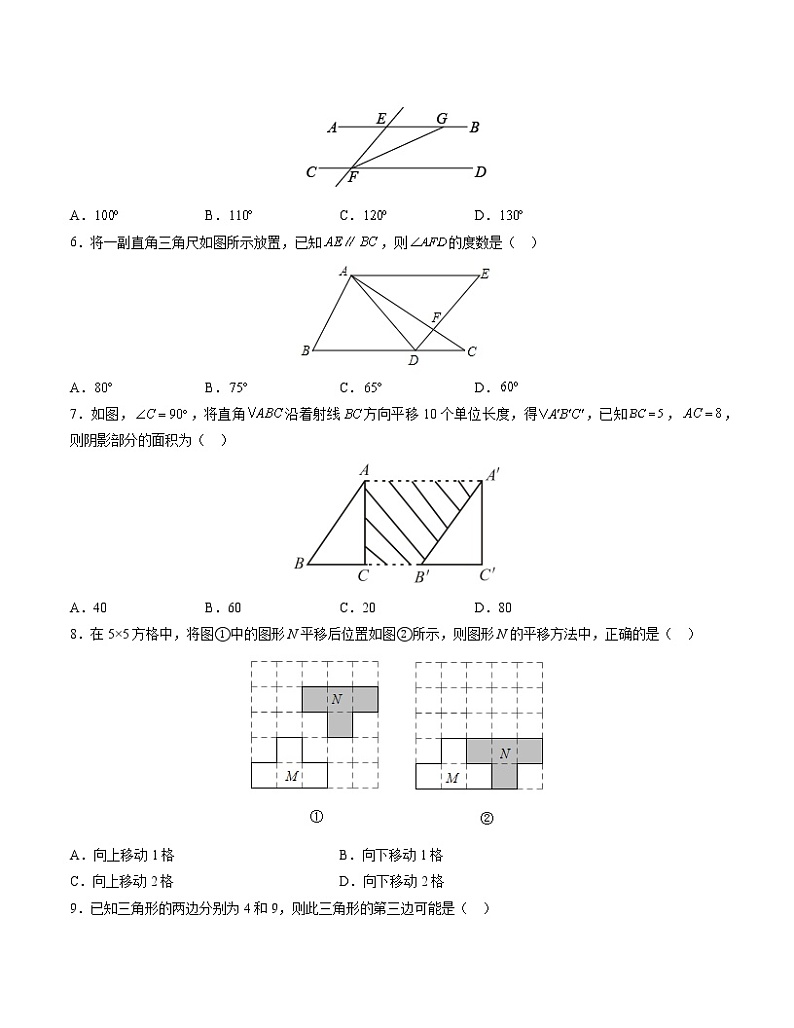
6．将一副直角三角尺如图所示放置，已知，则的度数是（    ）

A． B． C． D．
【答案】B
【解析】解：由三角板的性质可知．
∵，
∴，
∴．
∴．
故选：B．
7．如图，，将直角沿着射线方向平移10个单位长度，得，已知，，则阴影部分的面积为（    ）

A．40 B．60 C．20 D．80
【答案】B
【解析】解：∵△ABC的面积为：•CB•AC8×5＝20，
矩形 的面积：＝8×10＝80，
∴阴影部分的面积为80﹣20＝60，
故选：B．
8．在5×5方格中，将图①中的图形N平移后位置如图②所示，则图形N的平移方法中，正确的是（    ）

A．向上移动1格 B．向下移动1格
C．向上移动2格 D．向下移动2格
【答案】D
【解析】解：将图①中的图形N向下平移2个单位得到如图②所示图形．故选：D．
9．已知三角形的两边分别为4和9，则此三角形的第三边可能是（    ）
A．4 B．5 C．9 D．13
【答案】C
【解析】解：设此三角形的第三边为，
则由题意可得：，即
只有C选项符合题意，
故选：C
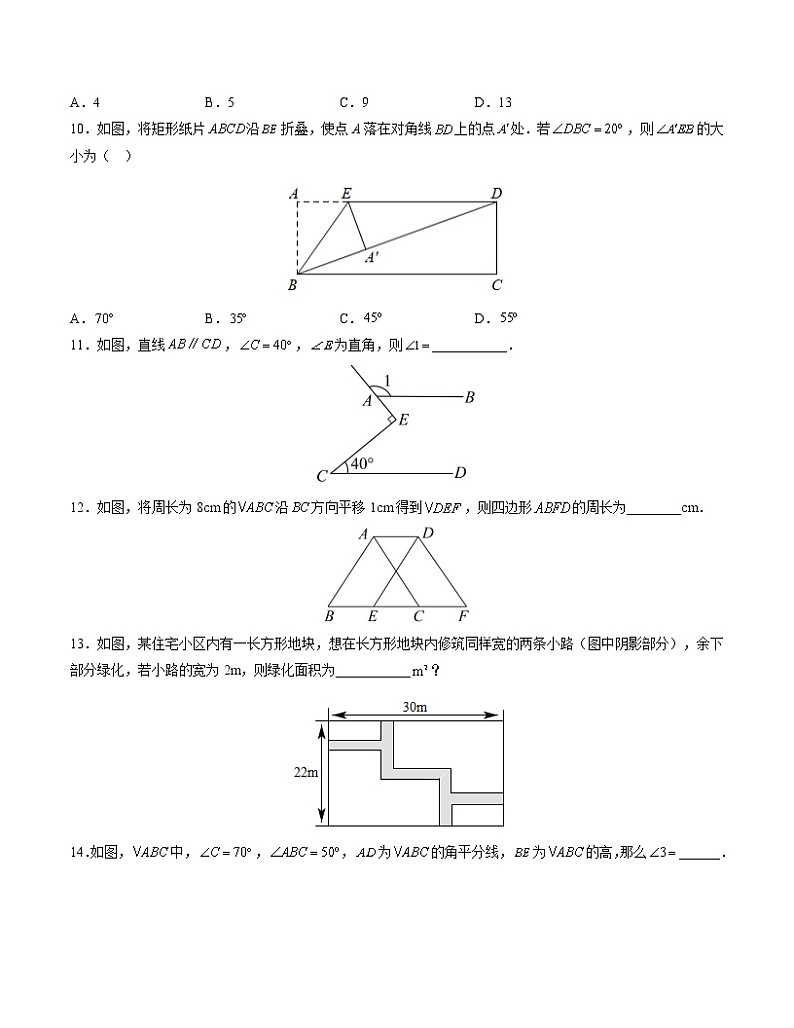
10．如图，将矩形纸片沿折叠，使点A落在对角线上的点处．若，则的大小为（    ）

A． B． C． D．
【答案】D
【解析】解：∵四边形是矩形，
∴，
由折叠的性质得：，，
∴，
∴．
故选：D．
11．如图，直线，，为直角，则___________．

【答案】
【解析】解：过点作，如下图：

则，
∴，
∴，
∴，
故答案为：
12．如图，将周长为8cm的沿方向平移1cm得到，则四边形的周长为________cm．

【答案】10
【解析】解：根据题意，将周长为8cm的沿向右平移1cm得到，
；又cm，
∴四边形的周长为cm．
故答案为：10．
13．如图，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条小路（图中阴影部分），余下部分绿化，若小路的宽为2m，则绿化面积为___________？

【答案】560
【解析】解：根据题意，得，故答案为：560．
14．如图，中，，，为的角平分线，为的高，那么______．

【答案】
【解析】解：∵，，
∴，
∵平分，
∴，
∵，
∴，
∴，
∴，
故答案为：．
15．如图，五边形是正五边形，、是两条对角线，则的度数为_______°．

【答案】36
【解析】解：∵五边形是正五边形，
∴，，
∴，
∴；
故答案为36．
16．多边形的每个内角都等于，则这个多边形是___________边形．
【答案】八
【解析】解：设多边形边数为n，
由题意可得每个外角都是，
由外角和定理可知，
解得．
即这个多边形是八边形．
故答案为：八．
17．如图，直线a，b直线c所截．

(1)当∠1＝∠3时，直线a，b平行吗？请说明理由．
(2)当∠2+∠3＝180°时，直线a，b平行吗？请说明理由．
【答案】(1)，理由见解析
(2)，理由见解析
【解析】（1）解：如图，

当∠1=∠3时，ab,理由如下：
∵∠1+∠2=180°，∠3+∠4=180°，∠1=∠3，
∴∠2=∠4，
∴ab；（2）当∠2+∠3=180°时，ab,理由如下：
∵∠2+∠3=180°，∠3+∠4=180°，
∴∠2=∠4，
∴ab；
18．如图，在三角形中，点D，E分别在上，且．

(1)与平行吗？为什么？
(2)若平分，求的度数．
【答案】(1)，理由见解析
(2)
【解析】（1），
理由：，
，                                
，
，
．
（2），
，
，
，                           
平分，
，
，
．
19．如图，在边长为个单位的正方形网格中，经过平移后得到，点的对应点为，根据下列条件，利用网格点和无刻度的直尺画图并解答，保留痕迹：

(1)画出，线段扫过的图形的面积为______；(2)在的右侧确定格点，使的面积和的面积相等，请问这样的点有______个？
【答案】(1)10；(2)4
【解析】（1）解：如图，即为所求，

线段扫过的面积为，故答案为：；
（2）解：如图，作，则点即为所求，共有个，故答案为：．
20．已知：如图，在△ABC中，AD是角平分线，E为边AB上一点，连接DE，∠EAD＝∠EDA，过点E作EF⊥BC，垂足为F．

(1)求证：DEAC；
(2)若∠DEF＝40°，∠B＝35°，求∠BAC的度数．
【答案】(1)见解析；(2)
【解析】（1）解：∵AD平分∠BAC，
∴∠BAD=∠CAD，
∵∠EAD=∠EDA，
∴∠EDA=∠CAD，
∴；
（2）解：∵EF⊥BD，
∴∠EFD=90°，
∴∠EDF=180°-∠DEF-∠EFD=50°，
∴∠BED=180°-∠B-∠BDE=95°，
∵，
∴∠BAC=∠BED=95°．

1．如图，点在的延长线上，下列条件不能判定的是（   ）

A． B． C． D．
【答案】C
【解析】解：A．根据内错角相等，两直线平行可判定，故此选项不合题意；B．根据同位角相等，两直线平行可判定，故此选项不合题意；C．根据内错角相等，两直线平行可判定，无法判定，故此选项符合题意；D．根据同旁内角互补，两直线平行可判定，故此选项不合题意；故选：C．
2．如图，，、、分别平分△ABC的外角、内角、外角．以下结论：①：②∠DAC=2∠ADB；③；④平分．其中正确的结论有（    ）

A．4个 B．3个 C．2个 D．1个
【答案】B
【解析】解：∵AD平分∠EAC，
∴∠EAC=2∠EAD，
∵∠EAC=∠ABC+∠ACB，∠ABC=∠ACB，
∴∠EAD=∠ABC，
∴ADBC，①正确；∵ADBC，
∴∠ADB=∠DBC，∠DAC=∠ACB，
∵BD平分∠ABC，∠ABC=∠ACB，
∴∠ABC=∠ACB=2∠DBC，
∴∠ACB=2∠ADB，
∴∠DAC=2∠ADB，
∴②正确；在△ADC中，∠ADC+∠CAD+∠ACD=180°，
∵CD平分△ABC的外角∠ACF，
∴∠ACD=∠DCF，
∵ADBC，
∴∠ADC=∠DCF，∠ADB=∠DBC，∠CAD=∠ACB
∴∠ACD=∠ADC，∠CAD=∠ACB=∠ABC=2∠ABD，
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°，
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD，∴③正确；∵BD平分∠ABC，
∴∠ABD=∠DBC，
∵∠ADB=∠DBC，∠ADC=90°-∠ABC，
∴∠ADB不等于∠CDB，∴④错误；即正确的有3个，
故选：B．
3．如图，在直角三角形ABC中，，将三角形ABC沿直线BC向右平移2cm得到三角形DEF，连接AE，有以下结论：①；②；③；④，其中正确的有（    ）

A．1个 B．2个 C．3个 D．4个
【答案】D
【解析】解：∵△ABC沿直线BC向右平移得到△DEF，
∴，，故①正确
∴，
∴，故②正确
∵，
∴，故③正确
∵△ABC沿直线BC向右平移得到△DEF，
∴，故④正确
故选：D．
4．如图，ABCD，PG平分∠EPF，∠A+∠AHP＝180°，下列结论：①CDPH；②∠BEP+∠DFP＝2∠EPG；③∠FPH＝∠GPH；④∠A+∠AGP+∠DFP﹣∠FPG＝180°；其中正确结论是（    ）

A．①②③④ B．①②④ C．①③④ D．①②
【答案】B
【解析】解：∵∠A+∠AHP＝180°，
∴PHAB，
∵ABCD，
∴CDPH，
故①正确；
∴ABCDPH，
∴∠BEP＝∠EPH，∠DFP＝∠FPH，
∴∠BEP+∠DFP＝∠EPF，
又∵PG平分∠EPF，
∴∠EPF＝2∠EPG，
∴∠BEP+∠DFP＝2∠EPG，
故②正确；∵∠GPH与∠FPH不一定相等，
∴∠FPH＝∠GPH不一定成立，故③错误；∵∠AGP＝∠HPG+∠PHG，∠DFP＝∠FPH，∠FPH+∠GPH＝∠FPG，∠FPG＝∠EPG，
∴∠A+∠AGP+∠DFP﹣∠FPG＝∠A+∠HPG+∠PHG+∠DFP﹣∠EPG
＝∠A+∠HPG+∠PHG+∠FPH﹣∠FPG＝∠A+∠HPG+∠PHG+∠FPH﹣（∠FPH+∠GPH）
＝∠A+∠PHG，
∵ABPH，
∴∠A+∠PHG＝180°，
即∠A+∠AGP+∠DFP﹣∠FPG＝180°．
故④正确；综上所述，正确的选项①②④，故选：B．
5．下列说法：① 四边形的四个外角的度数之比为4：3：2：1，则相应的内角之比为1：2：3：4；②若线段a、b、c，满足b+c>a，则以a、b、c为边一定能组成三角形；③ 三角形的高至多有两条在三角形外部；④在△ABC中，若∠A=∠B=∠C，则△ABC是钝角三角形； ⑤ 图形经过平移后，对应点的连线段互相平行且相等；⑥多边形的内角中，至多有3个角是锐角．其中正确的有（    ）个．
A．2 B．3 C．4 D．5
【答案】B
【解析】∵四边形外角和为360°，且四个外角的度数之比为4：3：2：1，
∴四个外角的度数分别为：144°、108°、72°、36°，
∵四边形的内角和与之对应的外角之和为180°，
∴四边形的四个内角分别为：36°、72°、108°、144°，
∴相应的内角之比为1：2：3：4，故①正确；∵三角形的三边满足：任意两边之和大于第三边，任意两边之差小于第三边，
∴当时，以a、b、c为边一定能组成三角形，故②错误；
∵锐角三角形的三条高均在三角形内部，钝角三角形有两条高在三角形外部，直角三角形有一条高在三角形内部，另外两条高为直角三角形的直角边，
∴③正确，
∵∠A+∠B+∠C=180°，且，
∴∠A=30°，∠B=90°，∠C=60°，
∴△ABC是直角三角形，故④错误，
∵水平位置的线段向右平移之后，对应点的连线段在同一条直线上，
∴故⑤错误，
∵假设多边形至少有四个内角为锐角，
∴与之对应的外角为四个钝角，
∴这四个钝角度数之和必然大于360°，
此结论与多边形外角和为360°相矛盾
故假设不成立，
∴多边形的内角中，至多有三个锐角，故⑥正确．
即正确的个数为：3，
故选：B．
6．如图，请添加一个条件，使得，添加一个符合要求的条件，可以是______．

【答案】∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°（答案不唯一）．
【解析】添加的条件可以是∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°．
∵∠BEF=∠C，
∴AB∥CD（同位角相等，两直线平行）．
∵∠AEC=∠C，
∴AB∥CD（内错角相等，两直线平行）．
∵∠BEC+∠C=180°，
∴AB∥CD（同旁内角互补，两直线平行）．
故答案为：∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°（答案不唯一）．
7．如图，已知∠1=72°，∠4=110°，∠3=70°，则∠2=____________．

【答案】72°
【解析】解：∵∠4＝110°，∠3＝70°，
∴∠3+∠4＝180°，
∴ab，
∴∠2＝∠1＝72°．
故答案为：72°．
8．如图，O是正六边形ABCDEF的中心，下列图形：△OCD，△ODE，△OEF，△OAF，△OAB，其中可由△OBC平移得到的有_________个．

【答案】2
【解析】解∶△OCD方向发生了变化，不是平移得到；△ODE符合平移的性质，是平移得到；△OEF方向发生了变化，不是平移得到；△OAF符合平移的性质，是平移得到；△OAB方向发生了变化，不是平移得到．故答案为∶2．
9．如图，在中，点D在边上，且，点E是的中点，交于一点G，连接，已知的面积是8，的面积是3，则的面积是__________．

【答案】
【解析】解：∵点E是的中点，
∴，
∵，的面积是8
∴，
∴，
∴．
故答案为：．
10．如图，五边形ABCDE是正五边形，且．若，则_______．

【答案】129°
【解析】解：如图，过点B作BF∥l2交DE于点F，

∵l1∥l2，
∴BF∥l1，
∵五边形ABCDE是正五边形，
∴∠ABC==108°，
∵BF∥l2，∠1=57°，∠2+∠CBF=180°，
∴∠ABF=∠1=57°，
∴∠CBF=∠ABC-∠ABF=108°-57°=51°，
∴∠2=180°-51°=129°，
故答案为：129°．
11．如图AF 与BD相交于点C，∠B=∠ACB， 且CD平分∠ECF．求证： ．
请完成下列推理过程：

证明：∵CD 平分∠ECF
∴∠ECD= _____ (                     )
∵∠ACB=∠FCD(                       ）
∴∠ECD=∠ACB(             ）
∵∠B=∠ACB
∴∠B=∠___(               )
∴ (               )．
【答案】∠FCD；角平分线的定义；对顶角相等；等量代换；ECD；等量代换； 同位角相等，两直线平行
【解析】证明：∵CD平分∠ECF
∴∠ECD∠FCD(角平分线的定义)
∵∠ACB∠FCD(对顶角相等)
∴∠ECD∠ACB(等量代换)
∵∠B=∠ACB
∴∠B=∠ECD( 等量代换)
∴(同位角相等，两直线平行) ．
12．如图，已知，，，三等分（即）．

(1)求的度数；(2)吗？为什么？
【答案】(1)；(2)，理由见解析．
【解析】（1）过点作，则，

∵，
∴，
∴
又∵，
∴，
∵三等分（即）
∴．
（2）由（1）知，
∴，
∴．
13．如图，在方格纸内将△ABC水平向右平移4个单位得到△．

(1)画出△；
(2)利用网格点和直尺画图：画出AB边上的中线CD，请在图中标出点D；(3)图中△ABC的面积是_________．
【答案】(1)见解析；(2)见解析；(3)8
【解析】（1）如图，△即为所求；
（2）
如图，中线CD即为所求；
（3）△ABC的面积=；故答案为：8；
14．如图，已知平分，且．

(1)求证：．
(2)若，，求的度数．
【答案】(1)见解析；(2)
【解析】（1）证明：平分，
，
又，
，
；
（2）解：，，
，
，
，
，
，
，
．
15．如图，在中，，在的延长线上取一点E，过点E作于点G，交于于点F，的角平分线相交于点H．

(1)求证：；
(2)延长EH交BC于点M，随着的变化，的大小会发生变化吗？如果有变化，求出与的数量关系；如果没有变化，求出的度数．
【答案】(1)见解析；(2)不会，
【解析】（1）∵，
∴．
∵，
∴．
（2）随着的变化，的度数不会变化，始终为．
∵，
∴．
∵BH平分，EH平分，
∴，
∴．
∵，
∴，
∴，
∴．

1．将一副三角板按如图放置，则下列结论①；②如果，则有；③如果，则有；④如果，必有，其中正确的有（    ）

A．①②③ B．①②④ C．③④ D．①②③④
【答案】D
【解析】∵∠1+∠2=∠3+∠2=90，
∴∠1=∠3，故①正确；
∵，
∴
∠E=60，
∴∠1=∠E，
∴AC∥DE，故②正确；
∵，
∴，
∵,
∴∠3=∠B,
∴,故③正确；∵，
∴∠CFE=∠C，
∵∠CFE+∠E=∠C+∠1，
∴∠1=∠E=,
∴∠2=90-∠1=，故④正确，
故选：D.

2．如图，是的角平分线，，是的角平分线，有下列四个结论： ①； ②； ③； ④．其中，正确的是（    ）

A．①② B．①②③ C．②③④ D．①②④
【答案】D
【解析】∵，
∴，，
∵BD平分，EF平分，
∴，，
∴，
，
∴，
故①②正确；
∴ 与不一定相等，
由题意可知，
∴与不一定相等，
故③错误；
∵，
∴与是等底等高的三角形，
∴，
∴，
故④正确，
∴①②④正确．
故选：D．
3．将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（    ）

A．16 B．24 C．30 D．40
【答案】D
【解析】设1号正方形的边长为x，2号正方形的边长为y，则3号正方形的边长为x+y，4号正方形的边长为2x+y，5号长方形的长为3x+y，宽为y-x，
由图1中长方形的周长为32，可得，y+2（x+y）+（2x+y）=16，
解得：x+y=4，
如图，
∵图2中长方形的周长为48，
∴AB+2（x+y）+2x+y+y-x=24，
∴AB=24-3x-4y，
根据平移得：没有覆盖的阴影部分的周长为四边形ABCD的周长，
∴2（AB+AD）=2(24-3x-4y+x+y+2x+y+y-x)=2（24-x-y）=48-2（x+y）=48-8=40，
故选：D．

4．如图，DC∥AB，AE⊥EF，E在BC上，过E作EC⊥DC，EG平分∠FEC，ED平分∠AEC．若∠EAD＋∠BAD＝180°，∠EDA＝3∠CEG，则下列结论：① ∠EAB＝2∠FEG；② ∠AED＝45°＋∠GEF；③ ∠EAD＝135°－4∠GEC；④ ∠EAB＝15°，其中正确的是（    ）

A．①②③④ B．①③④ C．①②④ D．①②③
【答案】D
【解析】解：∵EG平分∠FEC，
∴∠FEG＝∠CEG，
设∠FEG＝∠CEG＝α，
∴∠FEC＝2α，
∵∠EDA＝3∠CEG，
∴∠EDA＝3α，
∵EC⊥DC，，
∴EB⊥AB，∠C＝90°，
∴∠B＝90°，
∵AE⊥EF，
∴∠AEF＝90°，
∴∠AEC＝∠AEF＋∠FEC＝90°＋2α，
∵∠AEC＝∠B＋∠EAB＝90°＋∠EAB，
∴90°＋2α＝90°＋∠EAB，
∴∠EAB＝2α＝2∠FEG，
故①正确；∵ED平分∠AEC，
∴∠AED＝∠AEC＝（90°＋2α）＝45°＋α＝45°＋∠GEF，
故②正确；∵∠AED＝45°＋α，∠EDA＝3α，
∴∠EAD＝180°−∠AED−∠EDA＝180°−（45°＋α）−3α＝135°−4α＝135°−4∠GEC，
故③正确；∵∠EAD＋∠BAD＝180°，
∴∠EAB＋∠DAE＋∠EAD＝180°，
∴2α＋2（135°−4α）＝180°，
∴α＝15°，
∴∠EAB＝2α＝30°，
故④错误，
故选：D．
5．下列结论：①一个三角形的3个外角的度数之比为2：3：4，则相应的3个内角度数之比为；②在△ABC中，若∠A=2∠B=3∠C，则△ABC为直角三角形；③在图形的平移中，连接对应点的线段互相平行且相等；④一个多边形的边数每增加一条，这个多边形的内角和就增加；⑤一个五边形最多有3个内角是直角；⑥两条直线被第三条直线所截，同旁内角的角平分线互相垂直．其中错误结论有（    ）
A．3个 B．4个 C．5个 D．6个
【答案】B
【解析】解：①错误，设三角形的 3 个外角的度数分别为，，，
∴，解得
个外角的度数分别为，，，
其对应的内角分别为、、，
个内角度数之比为；②错误， 设，则，，，解得，
；
③错误， 根据平移的性质可知， 在图形的平移中， 连接对应点的线段互相平行或在一条直线上；
④正确，多边形的内角和为，边数每增加一条， 这个多边形的内角和就增加；⑤正确，五边形的内角和为，假设有四个角为直角， 则另外一个角的度数为，故有四个直角不成立，一个五边形最多有 3 个内角是直角；
⑥错误， 两条平行直线被第三条直线所截， 同旁内角的角平分线互相垂直 ．
综上所述：错误的个数为4个．
故选：B．
6．已知，平分，，，则___________．

【答案】
【解析】解：如图，作于，作于，

则，
设，则，，
平分，
，
设，则，
，
，，
，
，，
，，
又，
，
解得，
则，
故答案为：．
7．如图，点在线段上，且，点在上，若，，，则的度数为________．

【答案】
【解析】解：∵，
∴，
设，则，
∵，
∴，
∵在中，
，
又∵，，
∴．
∵，，
∴，
∵，
∴，
∴，
∴．
∵，，，
又∵，，，
∴，，
∵，
∴，
解得，，
∵，
∴，
故答案为：
8．从如图的五边形ABCDE纸片中减去一个三角形，剩余部分的多边形的内角和和是__________

【答案】 或或.
【解析】分三种情况：
①若剩余部分的多边形是四边形，则内角和为360°，
②若剩余部分的多边形是五边形，则内角和为，
③若剩余部分的多边形是六边形，则内角和为，
故答案为： 或或.

9．已知，的平分线与的平分线相交于点F．

(1)在图1中，求证：
①；②；(2)如图2，当，时，请你写出与之间的关系，并加以证明；(3)当，，且时，请你直接写出的度数（用含m，n的式子表示）
【答案】(1)证明见详解；
(2)，证明见详解；(3)
【解析】（1）证明：①如图１，过点作

，
，
，


，

证明：②如图１，过点作


，


，
即
（2）解：关系式为，
证明：设，
，时，且平分，平分，
，

由（１）得，
，
，
，
即，
，

（3）解：设则
，，
由（１）可得
，
，
，
，
，
即的度数（用含m，n的式子表示）表示为
10．如图，直线，点A为直线a上的动点，点B为直线a、b之间的定点，点C为直线上的定点．

(1)当点A运动到图1所示位置时，容易发现之间的数量关系为 ；
(2)如图2，当时，作等边，平分，交直线a于点M，平分，交直线b于点N，将绕点B转动，且始终在的内部时，的值是否发生变化？若不变，求其值，若变化，说明理由；
(3)点F为直线a上一点，使得，的平分线交直线a于点G，当点A在直线a上运动时（A，B，C三点不共线），探究并直接写出与之间的数量关系．（本问中的角均为小于180°的角）
【答案】(1)∠ABC＝∠DAB+∠BCE；
(2)不变化，；(3)∠ECB＝2∠FBG或，理由见解析．
【解析】（1）解：作BH∥a，如图1：

则，
∵，
∴，
∴，
∴，
故答案为：；
（2）的值不变化，理由如下：
如图2：

∵，
∴，
∵，
∴，
∵，
∴，即，
由（1）得，
∴；
（3）当点F在点A的右侧时，如图3：

，理由如下：
∵，
由（1）知，
∵的平分线交直线a于点G，
∴，
∵，
∴，
∵，
∴，
∴，
即．
当点F在点A的左侧时，如图4，
，理由如下：

∵的平分线交直线a于点G，
∴．
∵，，
∴．
由（1）知，
∴，
∴，
∴，
∴．
综上可知，与之间的数量关系为：或．