




- 第二十六章 反比例函数复习【知识梳理】——2022-2023学年人教版数学九年级下册单元综合复习课件PPT 课件 0 次下载
- 第二十六章 反比例函数【单元检测】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版) 试卷 0 次下载
- 第二十七章相似复习【知识梳理】——2022-2023学年人教版数学九年级下册单元综合复习课件PPT 课件 0 次下载
- 第二十七章 相似【题型专练】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版) 试卷 0 次下载
- 第二十七章 相似【单元检测】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版) 试卷 0 次下载
第二十六章 反比例函数【题型专练】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版)
展开第二十六章 反比例函数
考查题型一 反比例函数的定义
典例1.(2022·山东·泰安市泰山区树人外国语学校九年级阶段练习)下列问题中,两个变量成反比例函数的是( )
A.矩形面积固定,长和宽的关系 B.矩形周长固定,长和宽的关系
C.正方形面积和边长之间的关系 D.正方形周长和边长之间的关系
【答案】A
【分析】根据矩形的面积、周长与其长和宽的关系,正方形面积、周长与其边长的关系,列出关系式,根据反比例函数的定义判断即可.
【详解】解:A、,故长和宽成反比例函数,选项符合题意;
B、,故长和宽成一次函数,选项不符合题意;
C、,故正方形面积和边长不成反比例函数,选项不符合题意;
D、,故正方形周长和边长成正比例函数,选项不符合题意;
故选:A.
【点睛】本题考查了反比例函数的解析式,根据题意列出函数关系式是解答本题的关键.
变式1-1.(2022·湖南省岳阳开发区长岭中学九年级阶段练习)下列函数关系式中,y不是x的反比例函数的是( )
A. B. C. D.
【答案】C
【分析】根据反比例函数的定义和等价形式进行判断即可.
【详解】A、,是反比例函数,不符合题意;
B、,是反比例函数,不符合题意;
C、,不是反比例函数,符合题意;
D、,是反比例函数,不符合题意;
故选C.
【点睛】本题考查反比例函数的定义.熟练掌握反比例函数的定义:和等价形式:,是解题的关键.
变式1-2.(2022·山东·东平县实验中学九年级阶段练习)下列函数中,是反比例函数的是( )
A.y=x B.y=-2x+3 C.y= D.y=-
【答案】C
【分析】根据反比例函数的定义,逐项判断即可求解.
【详解】解:A、不是反比例函数,故本选项不符合题意;
B、不是反比例函数,故本选项不符合题意;
C、是反比例函数,故本选项符合题意;
D、不是反比例函数,故本选项不符合题意;
故选:C
【点睛】本题考查了反比例函数的定义,熟练掌握反比例函数的一般式是(k≠0)是解题的关键.
变式1-3.(2022·安徽·定远县第一初级中学九年级阶段练习)下列函数:①y=x-2;②;③;④;y是x的反比例函数的个数有( )
A.0个 B.1个 C.2个 D.3个
【答案】B
【分析】根据反比例函数的定义:进行判断即可.
【详解】解:由反比例函数的定义可知:是反比例函数,其余都不是;
故选B.
【点睛】本题考查反比例函数的定义.熟练掌握反比例函数的定义是解题的关键.
考查题型二 根据反比例函数的定义求参数
典例2.(2022·湖南·李达中学九年级开学考试)若是反比例函数,则a的取值为( )
A.1 B.﹣1 C.±1 D.任意实数
【答案】A
【分析】根据反比例函数的定义直接解答即可.
【详解】解:∵是反比例函数,
∴且a+1≠0,
解得a=1.
故选:A.
【点睛】本题考查了反比例函数的定义,重点是知道(k≠0)是反比例函数.
变式2-1.(2021·山东·寿光市圣城中学九年级阶段练习)已知函数是反比例函数,则的值为( ).
A.1 B.-1 C.±1 D.±2
【答案】A
【分析】根据反比例函数的定义,反比例函数的一般式是y= (k≠0),即可得到关于n的方程,解方程即可求出n.
【详解】解:∵函数是反比例函数,
∴n+1≠0且n2−2=−1,
∴n=1,
故答案选A
【点睛】本题考查了反比例函数的定义,反比例函数解析式的一般式y= (k≠0),特别注意不要忽略k≠0这个条件.
变式2-2.(2022·安徽·合肥市五十中学西校九年级阶段练习)如果双曲线经过点,那么此双曲线也一定经过( )
A. B. C. D.
【答案】D
【分析】双曲线经过点,可知点的横纵坐标的积为k=-6,根据反比例函数图象上的点的坐标的特点可知双曲线经过的点.
【详解】解:双曲线经过点,
∴2×(-3)=-6,
又∵(-3)×2=-6,
∴双曲线也经过点(-3,2).
故选:D.
【点睛】本题考查了反比例函数图象上点的坐标特征,只要点在函数的图象上,则一定满足函数的解析式.反之,只要满足函数解析式就一定在函数的图象上.
变式2-3.(2022·湖南·九年级单元测试)如果反比例函数的图象经过点,则( )
A.18 B. C.16 D.
【答案】D
【分析】直接把点代入反比例函数的解析式,即可求出k的值.
【详解】解:∵反比例函数的图象经过点,
∴,
∴;
故选:D.
【点睛】本题考核反比例函数的解析式,解题的关键是运用反比例函数的性质求参数.
考查题型三 求反比例函数的函数值
典例3.(2022·黑龙江·哈尔滨市第八十四中学校一模)若点A(2,a)在反比例函数的图象上,则a的值为( )
A.2 B.3 C.4 D.6
【答案】B
【分析】直接将点(2,a)代入即可求出a的值.
【详解】解:由题意知,,
解得:a=3.
故选:B.
【点睛】本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.
变式3-1.点A(﹣2,m)在函数的图象上,则m的值是( )
A. B. C.2 D.﹣2
【答案】B
【分析】将x=﹣2代入一次函数解析式中求出y值,此题得解.
【详解】解:∵点A(﹣2,m)在函数的图象上,
∴.
故选:B.
【点睛】此题主要考查了反比例函数已知横坐标求纵坐标,熟练掌握反比例函数的性质是解题的关键.
变式3-2.(2022·广西桂林·九年级期末)已知点在反比例函数的图象上,则的值为( )
A.-2 B.2 C.-3 D.3
【答案】C
【分析】将点代入函数求解即可.
【详解】解:将点代入函数得,,
故选:C
【点睛】此题考查了反比例函数的有关性质,解题的关键是掌握反比例函数的有关性质.
变式3-3.(2022·江西吉安·九年级期末)点,是反比例函数的图象上两点,则mn的值为( )
A.2 B.-3 C.6 D.-6
【答案】D
【分析】将,代入中,即可求出m、n的值,再相乘即可.
【详解】解:将,代入中,得:
,,
∴.
故选:D.
【点睛】本题考查反比例函数图象上点的坐标特征,代数式求值.掌握反比例函数图象上点的坐标满足其解析式是解题关键.
考查题型四 比例系数K与面积问题
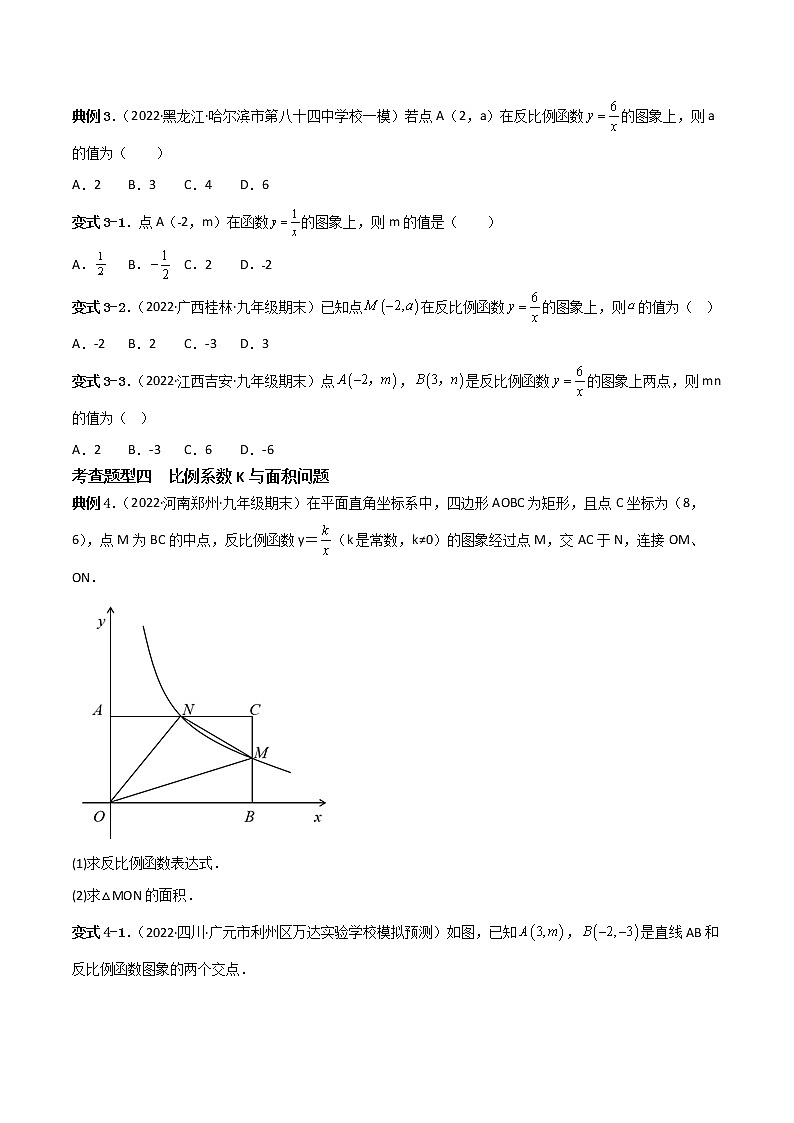
典例4.(2022·河南郑州·九年级期末)在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),点M为BC的中点,反比例函数y=(k是常数,k≠0)的图象经过点M,交AC于N,连接OM、ON.
(1)求反比例函数表达式.
(2)求△MON的面积.
【答案】(1)y=;
(2)18
【分析】(1)根据矩形性质和坐标与图形性质可得点M的坐标和点N的纵坐标,将M点坐标代入y=即可求得函数解析式;
(2)求得点N的坐标,根据反比例函数系数k的几何意义得,再由求解即可.
(1)
解:∵四边形AOBC为矩形,
∴AC∥x轴,BC∥y轴,
∵点C坐标为(8,6),点M为BC的中点,N在AC上,
∴点M坐标为(8,3),点N的纵坐标为6,
将M(8,3)代入y=中,得:k=3×8=24,
故反比例函数表达式为y=;
(2)
解:当y=6时,由6=得:x=4,
∴点N的坐标为(4,6),
∵AN⊥y轴,BM⊥x轴,
∴=12,又,,
∴=48-12-12-6=18,
即△MON的面积是18.
【点睛】本题考查反比例函数与几何综合,涉及矩形性质、坐标与图形、反比例函数图象上点的坐标特征、三角形的面积公式等知识,熟练掌握待定反比例函数图象上点的坐标特征,利用数形结合思想求解是解答的关键.
变式4-1.(2022·四川·广元市利州区万达实验学校模拟预测)如图,已知,是直线AB和反比例函数图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x在什么范围时,直线AB在双曲线的下方;
(3)求出三角形AOB的周长和面积.
【答案】(1)直线AB 的解析式为y=x-1;反比例函数解析式为y=;
(2)x<-2或0<x<3
(3);
【分析】(1)运用待定系数法,根据A(3,m),B(-2,-3),即可得到直线AB和反比例函数的解析式;
(2)根据直线AB在双曲线的下方,即可得到x的取值范围;
(3)根据两点间距离公式求出AO,BO,AB的长,即可得到三角形AOB的周长;求出直线AB与x轴交点坐标,根据三角形面积公式可求出三角形AOB的面积.
(1)
设反比例函数解析式为y=,
把B(-2,-3)代入,可得k=-2×(-3)=6,
∴反比例函数解析式为y=;
把A(3,m)代入y=,可得3m=6,
即m=2,
∴A(3,2),
设直线AB 的解析式为y=ax+b,
把A(3,2),B(-2,-3)代入,可得,
解得,
∴直线AB 的解析式为y=x-1;
(2)
由图象可得,当x满足:x<-2或0<x<3时,直线AB在双曲线的下方;
(3)
∵,
∴
∴三角形AOB的周长=
对于y=x-1,当y=0时,x=1,
∴直线y=x-1与x轴的交点坐标为(1,0)
∴
【点睛】本题考查了用待定系数法确定反比例函数的比例系数k,求出函数解析式;要能够熟练借助直线和y轴的交点运用分割法求得不规则图形的面积.
变式4-2.(2022·广东·揭西县宝塔实验学校模拟预测)如图,在平面直角坐标系xOy中,直线y=ax+b与双曲线交于A(1,3),B(3,m)两点,与x轴交于点C,与y轴交于点D,连接OA,OB.
(1)求a,b,k的值;
(2)求△OAB的面积;
(3)在x轴上是否存在点P,使△PCD的面积等于△OAB的面积的3倍,若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)a=-1,b=4,k=3
(2)4
(3)存在,P(-2,0)或(10,0)
【分析】(1)把A点的坐标代入反例函数解析式即可求出反比例函数解析式,进而得出B的坐标,把A、B的坐标代入一次函数解析式即可求出一次函数解析式;
(2)先由直线解析式求得D(0,4),C(4,0),根据△AOB的面积=△BOD的面积-△AOD的面积求得△AOB的面积;
(3)根据题意得到PC•OD=12,即=12,即可求得PC的长,从而求得P的坐标.
(1)
将点A(1,3)代入y=得:3=,
解得k=3,
故反比例函数的表达式为:y=,
将点B(3,m)代入y=得:m=1,
故点B(3,1),
将点A(1,3),B(3,1)代入y=ax+b,得,
解得;
故a=-1,b=4,k=3;
(2)
由一次函数y=-x+4可知,D(0,4),C(4,0),
则△AOB的面积=△BOD的面积-△AOD的面积=-=4;
(3)
∵△PCD的面积等于△OAB的面积的3倍.
∴PC•OD=12,即=12,
∴PC=6,
∴P(-2,0)或(10,0).
【点睛】本题主要考查了反比例函数和一次函数的交点问题,用待定系数法求反比例函数和一次函数的解析式的应用,主要考查学生的计算能力.
变式4-3.(2022·河南安阳·二模)如图,直线与反比例数(,且)的图象交于点A,点A的横坐标是1.
(1)求点A的坐标及反比例函数的解析式.
(2)若B是反比例函数(,且)图象上的一点,且点B的纵坐标是1,连接OB,AB,求的面积.
【答案】(1),
(2)
【分析】(1)将点A横坐标代入直线解析式求得纵坐标,即可求得 A 的坐标,进而代入反比例函数解析式即可求解;
(2)根据B的纵坐标,代入反比例函数求得B的横坐标,过点A,B,分别作x轴的垂线,AD,BC,根据的面积等于梯形ABCD的面积即可求解.
(1)
解:将x=1代入,解得,即,
将代入,得,
反比例函数的解析式;
(2)
如图,过点A,B,分别作x轴的垂线,AD,BC,垂足分别为D、C,
点B的纵坐标是1,将代入,得 ,
,
,
,
,
.
【点睛】本题考查了一次函数与反比例数综合,反比例函数的几何意义,分别求得的坐标是解题的关键.
考查题型五 一次函数与反比例函数的交点问题
典例5.(2022·山东·济南育英中学九年级阶段练习)如图,在平面直角坐标系中,直线与双曲线交于A,B两点,已知点A的横坐标为2.
(1)求k的值;
(2)直接写出关于x的不等式的解集.
【答案】(1)
(2)关于x的不等式的解集是或
【分析】(1)求出A(2,5),代入,即得;
(2)联立解析式求出B(,),然后根据图象,即可求得.
(1)
解:在中,令,得,
A(2,5),
,
;
(2)
解:联立得或,
B(,),
由图象可知:关于x的不等式的解集是或.
【点睛】本题是一次函数与反比例函数的交点问题,考查了一次函数图象上点的坐标特征,用待定系数法求反比例函数的解析式,解题的关键是利用数形结合解决相关问题.
变式5-1.(2022·湖北·大悟县实验中学九年级阶段练习)如图,已知一次函数与反比例函数的图象在第一、三象限分别交于,两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)已知x轴负半轴上有一点M,能使,求M的坐标.
【答案】(1)一次函数的解析式为,反比例函数的解析式为
(2)M的坐标为
【分析】(1)利用待定系数法解题,把代入反比例函数中,解得m的值,进而求出点B的坐标,再把,代入即可求解;
(2)设一次函数的图象与x轴交于点C,求出点C的坐标,利用求出,进而求出,设M的坐标为,可得,利用列出等式,即可求解.
(1)
解:把代入,得,
解得,
∴反比例函数的解析式为;
把代入,得
解得,
∴,
把,代入,
得:,
解得:,
∴一次函数的解析式为.
(2)
解:设一次函数的图象与x轴交于点C,
令,得,
解得,即点C的坐标为,
∴,
∴,
∴,
设M的坐标为,
则,
∴,
解得,
∴ M的坐标为.
【点睛】本题考查反比例函数与一次函数的综合应用,涉及待定系数法求函数解析式、三角形面积公式等,解题的关键是熟练掌握平面直角坐标系内三角形面积的计算方法.
变式5-2.(2022·安徽·合肥市小庙中学九年级阶段练习)如图,一次函数的图象与反比例函数的图象交于点,与x轴交于点.
(1)求一次函数和反比例函数的表达式;
(2)若直线与直线AB交于点C,与双曲线交于点D,根据图象,直接写出不等式的解集.
【答案】(1)一次函数的表达式为;反比例函数的表达式为;
(2)不等式的解集:.
【分析】(1)运用待定系数法求出在一次函数的表达式,从而求出点A的坐标,再运用待定系数法即可求出反比例函数的表达式;
(2)根据反比例函数的性质求出点D的横坐标,然后根据函数的图象即可求得.
(1)
解:由点在一次函数上,得,
∴一次函数的表达式为;
由点在上,得,
∴,
把代入得,
∴反比例函数的表达式为:;
(2)
解:,即,
当时,,解得,
观察图象,不等式的解集:.
【点睛】本题考查了待定系数法求函数解析式及反比例函数与一次函数图象交点的问题,求得点的坐标是解题的关键.
变式5-3.(2022·浙江·桐乡市高桥镇高桥初级中学九年级期中)如图,一次函数与反比例函数的图象交于两点.过点A作轴,垂足为C,且,
(1)求一次函数与反比例的数的解析式;
(2)若是函数图象上的两点,且写出实数p的取值范围.
【答案】(1)反比函数的解析式为,一次函数解析式为
(2)实数p的取值范围是或
【分析】(1)根据反比例函数系数k的几何意义求得k=6,进而求得A、B的坐标,然后利用待定系数法可得一次函数解析式;
(2)根据反比例函数的性质即可得.
(1)
∵点A在反比例函数的图象上,轴,垂足为C,且,
∴,
∴,
∴反比函数的解析式为,
把代入反比例函数,可得m=3,n=-3,
∴,
把代入一次函数,可得,
解得,
∴一次函数解析式为;
(2)
由图可得,当在第三象限时,
要使,则;
当在第一象限时,
要使,则;
故实数p的取值范围是或.
【点睛】本题考查了一次函数与反比例函数的交点问题,解决本题的关键是学会利用待定系数法确定函数解析式、反比例函数图象上点的坐标特征和反比例函数的性质.
考查题型六 实际问题与反比例函数
典例6.(2022·山东师范大学第二附属中学九年级阶段练习)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图像如图所示.
(1)求这个函数的解析式;
(2)当气体体积为时,气压是多少?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气体的体积应不小于多少?
【答案】(1)
(2)气压是
(3)为了安全起见,气体的体积应不少于
【分析】(1)设,将点代入,得,进行计算即可得;
(2)当时,,即可得;
(3)当时,,即可得.
(1)
解:设,
将点代入,得,
,
即这个函数的解析式为;
(2)
解:当时,,
即当气体体积为时,气压是;
(3)
解:当时,,
所以为了安全起见,气体的体积应不少于.
【点睛】本题考查了反比例函数的应用,解题的关键是掌握反比函数的图像和性质.
变式6-1.(2022·陕西西安·九年级期末)西安市某校为进一步预防“新型冠状病毒”,对全校所有的教室都进行了“熏药法消毒”处理,已知该药物在燃烧释放过程中,教室内空气中每立方米的含药量y(mg)与燃烧时间x(min)之间的函数关系如图所示,其中当x<6时,y是x的正比例函数,当时,y是x的反比例函数,根据图象提供的信息,解答下列问题:
(1)求当x≥6时,y与x的函数关系式.
(2)求点A的坐标.
(3)药物燃烧释放过程中,若空气中每立方米的含药量不小于1.5mg的时间超过30分钟,即为有效消毒,请问本题中的消毒是否为有效消毒?
【答案】(1)
(2)
(3)是有效消毒
【分析】(1)设与的函数关系式为,根据点,利用待定系数法即可得;
(2)根据(1)的结果,求出时,的值,由此即可得;
(3)先利用待定系数法求出所在直线的表达式,再求出时的值,由此即可得.
(1)
解:设与的函数关系式为,
将点代入得:,
解得,
则当时,与的函数关系式为.
(2)
解:对于反比例函数,
当时,,
则点的坐标为.
(3)
解:设所在直线的表达式为,
将点代入得:,解得,
则所在直线的表达式为,
将代入得:,解得,
将代入得:,解得,
因为,
所以本题中的消毒是有效消毒.
【点睛】本题考查了反比例函数和正比例函数的应用,熟练掌握待定系数法是解题关键.
变式6-2.(2022·广东佛山·二模)某种消毒药喷洒释放完毕开始计时,药物浓度与时间之间的关系如下:
时间
2
4
12
药物浓度
18
9
3
(1)求关于的关系式;
(2)当药物浓度不低于并且持续时间不少于时消毒算有效,问这次消毒是否有效?.
【答案】(1)
(2)此次消毒有效,理由见解析
【分析】(1)根据表格数据可知与的乘积是个定值为36,由此即可求解;
(2)先求出当时,,从而得到有效时间为6min,由此即可得到答案.
(1)
解:由表格可知与的乘积是个定值为36,
∴可知x与y呈反比例函数关系,
∴;
(2)
解:当时,,
∵,
∴此次消毒有效.
【点睛】本题主要考查了反比例函数的实际应用,正确理解题意是解题的关键.
变式6-3.(2022·福建省福州屏东中学一模)“姹紫嫣红苗木种植基地”尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元/株的果苗,售后经过统计得到此果苗,单价在第x天(x为整数)销售的相关信息,如图表所示:
销售量n(株)
n=-x+50
销售单价
m(元/株)
当时,m=______
当时,
(1)求出表中当时,m与x间的函数关系式;
(2)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”.试问:基地负责人这次为“精准扶贫”捐赠多少钱?
【答案】(1)
(2)基地负责人这次为“精准扶贫”捐赠元
【分析】(1)利用待定系数法求解即可;
(2)设该基地第x天的利润为W,根据利润=(售价-成本)×数量列出W关于x的关系式,然后根据二次函数与反比例函数的性质求解即可.
(1)
解:由函数图象可知当时,m与x间的函数关系式满足一次函数关系式,故可设当时,m与x间的函数关系式为,
∵,
∴,
∴当时,m与x间的函数关系式为;
(2)
解:设该基地第x天的利润为W,
由题意得:,
当时,,
∵,
∴当时,W最大为;
当时,
∵,
∴随x增大而减小,即W随x增大而减小,
∴当时,W最大为580,
∵,
∴基地负责人这次为“精准扶贫”捐赠元.
【点睛】本题主要考查了一次函数,二次函数,反比例函数的应用,正确理解题意列出函数关系式是解题的关键.
第二十七章 相似【题型专练】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版): 这是一份第二十七章 相似【题型专练】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版),文件包含第二十七章相似题型专练解析版docx、第二十七章相似题型专练原卷版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
第二十六章 反比例函数【单元检测】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版): 这是一份第二十六章 反比例函数【单元检测】——2022-2023学年人教版数学九年级下册单元综合复习(原卷版+解析版),文件包含第二十六章反比例函数单元检测解析版docx、第二十六章反比例函数单元检测原卷版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
第6章 图形的相似【题型专练】——2022-2023学年苏科版数学九年级下册单元综合复习(原卷版+解析版): 这是一份第6章 图形的相似【题型专练】——2022-2023学年苏科版数学九年级下册单元综合复习(原卷版+解析版),文件包含第6章图形的相似题型专练2022-2023学年苏科版数学九年级下册单元综合复习解析版docx、第6章图形的相似题型专练2022-2023学年苏科版数学九年级下册单元综合复习原卷版docx等2份试卷配套教学资源,其中试卷共92页, 欢迎下载使用。












