单元复习07 计数原理【过知识】（课件）- 2022-2023学年高二数学单元复习（苏教版2019选择性必修第二册）

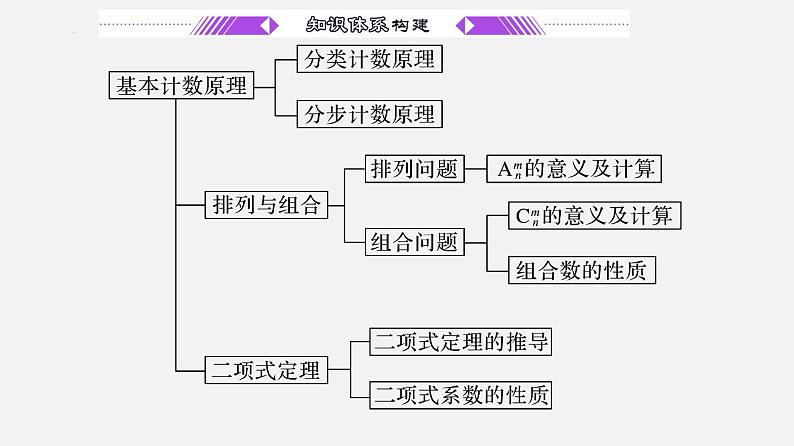
这是一份单元复习07 计数原理【过知识】（课件）- 2022-2023学年高二数学单元复习（苏教版2019选择性必修第二册），共60页。PPT课件主要包含了知识点归纳，考点题型探究，答案504，答案480，答案B，答案C，答案840，答案D，两式相乘得，所以m只能等于2等内容，欢迎下载使用。

【例1】 用0,1,2,3,4,5,6这7个数字可以组成　　　个无重复数字的四位偶数. 
答案 420　解析 要完成的“一件事”为“组成无重复数字的四位偶数”,所以千位数字不能为0,个位数字必须是偶数,且组成的四位数中四个数字不重复,因此应先分类,再分步.
(方法1)第1类,当千位数字为奇数时,即取1,3,5中的任意一个时,个位数字可取0,2,4,6中的任意一个,百位数字不能取与这两个数字重复的数字,十位数字不能取与这三个数字重复的数字.根据分步乘法计数原理,有3×4×5×4=240(个)数.第2类,当千位数字为偶数且不为0时,即取2,4,6中的任意一个时,个位数字可以取除首位数字外的任意一个偶数数字,百位数字不能取与这两个数字重复的数字,十位数字不能取与这三个数字重复的数字.根据分步乘法计数原理,有3×3×5×4=180(个)数.根据分类加法计数原理,共可以组成240+180=420(个)无重复数字的四位偶数.(方法2　排除法)先定个位数有4种取法,再定另外3位数有 =120(种)取法,共有480种.其中0作千位,其余数作个位不合题意,有3× =60(种)取法.故应有480-60=420(种)取法.故共可以组成420个无重复数字的四位偶数.
解题心得解决较为复杂的计数问题,一般要将两个计数原理综合应用.使用时要做到合理分类,准确分步:处理计数问题,应紧扣两个原理,根据具体问题首先弄清楚是“分类”还是“分步”,要搞清楚“分类”或者“分步”的具体标准.分类时需要满足两个条件:①类与类之间要互斥(保证不重复);②总数要完备(保证不遗漏),也就是要确定一个合理的分类标准.分步时应按事件发生的连贯过程进行分析,必须做到步与步之间互相独立,互不干扰,并确保连续性.
对点训练1如图,一个地区分为5个行政区域,现给该地区的地图着色,要求相邻区域不得使用同一种颜色,现有4种颜色可供选择,则不同的着色方法共有　　　　种. 
答案 72　解析 (方法1)由题图可知,2区与4区不相邻,3区与5区不相邻,且不相邻的区域可用同1种颜色涂色,所以最少可用3种颜色,故可根据选用颜色的种数进行分类.第1类,使用3种颜色,则2区与4区同色,3区与5区同色,可分三步进行涂色:第1步,涂2区与4区,有4种颜色可选;第2步,涂3区与5区,有3种颜色可选(除涂2区、4区的颜色);第3步,涂1区,有2种颜色可选(除前2步所选的颜色).由分步乘法计数原理知,该类涂色方法共有4×3×2=24(种).
第2类,使用4种颜色,2区与4区同色,3区与5区不同色,可分4步进行涂色:第1步,涂2区与4区,有4种颜色可选;第2步,涂1区,有3种颜色可选;第3步,涂3区,有2种颜色可选;第4步,涂5区,有1种颜色可选.由分步乘法计数原理可知,该类涂色方法共有4×3×2×1=24(种).第3类,使用4种颜色,3区与5区同色,2区与4区不同色,同理可得该类涂色方法共有24种.综上,由分类加法计数原理可知,不同的涂色方法共有24+24+24=72(种).(方法2)因为1区与其他4个区都相邻,首先考虑1区,有4种涂法.若2区与4区同色,有3种涂色,此时3区与5区均有2种涂法,涂法种数为4×3×2×2=48;若2区与4区不同色,先涂2区,有3种方法,再涂4区,有2种方法,此时3区与5区都只有1种涂法,涂法种数为4×3×2×1×1=24.因此,满足条件的涂色方法共有48+24=72(种).
解题心得1.排列数和组合数公式要注意m∈N*,n∈N*,且n≥m,由此确定m,n的范围,求解后要验证所得结果是否符合题意.2.解排列数(组合数)不等式(方程)时,应先利用计算公式将排列数(组合数)的形式转化为常规代数不等式(方程)的形式,然后求解.
解 (1)由排列数和组合数公式,原方程可化为即(x-3)(x-6)=40,整理得x2-9x-22=0,解得x=11或x=-2.经检验知x=11是原方程的根,x=-2是原方程的增根.∴方程的根为x=11.(2)原不等式可化为(n-2)(n-3)>2-n,整理得n2-4n+4>0,即(n-2)2>0,解得n≠2.∵n-2≥2,∴n≥4,∴原不等式的解集为{n|n≥4,n∈N*}.
考向1　在与不在问题——特殊元素(或位置)优先法【例3】 6人站成一排,其中甲不能站在排头,乙不能站在排尾的不同排法共有　　　　种. 
解题心得解此类问题常用“元素分析法”“位置分析法”.元素分析法——即以元素为主,优先考虑特殊元素的要求,再考虑其他元素;位置分析法——即以位置为主,优先考虑特殊位置的要求,再考虑其他位置.
变式发散6人站成一排,则甲既不站排头又不站排尾的站法有　　　　　种. 
对点训练3 6个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有(　　)A.192种B.216种C.240种D.288种
考向2　相邻问题——捆绑法【例4】 3名男生、3名女生排成一排,男生必须相邻,女生也必须相邻的排法种数为(　　)A.2B.9C.72D.36
解题心得在实际排列问题中,某些元素要求必须相邻时,可以先将这些元素看成一个整体,与其他元素排列后,再考虑相邻元素的内部排序,这种方法称为“捆绑法”.
对点训练4某小区有排成一排的7个车位,现有3辆不同型号的车需要停放,如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为(　　)A.16B.18C.24D.32
答案 C解析 将4个车位捆绑在一起,看成一个元素,先排3辆不同型号的车,在3个车位上任意排列,有 =6(种)方法,再将捆绑在一起的4个车位插入4个空位中,有4种方法,故共有4×6=24(种)方法.
考向3　不相邻问题——插空法【例5】 某校高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求2个舞蹈节目不连排,则不同排法的种数是(　　)A.1 800 B.3 600C.4 320D.5 040
解题心得某些元素要求不相邻时,可以先安排其他元素,再将这些不相邻元素插入已排好的元素的空隙或两端位置,这种方法称为“插空法”.
对点训练5某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,同类节目不相邻的排法种数是(　　)A.72B.120 C.144D.168
考向4　定序问题——等几率法【例6】 有4名男生,3名女生,其中3名女生高矮各不相同,将7名学生排成一行,要求从左到右,女生从矮到高排列(不一定相邻),不同的排法共有　　　　　种. 
对点训练6 7个人排成一队参观某项目,其中A,B,C三人进入展厅的次序必须是先B再A后C,则不同的列队方式种数为(　　)A.120B.240 C.420D.840
【例7】 某市工商局对35种商品进行抽样检查,已知其中有15种不合格商品.现从35种商品中选取3种.(1)其中某一种不合格商品必须在内,不同的取法有多少种?(2)其中某一种不合格商品不能在内,不同的取法有多少种?(3)恰有2种不合格商品在内,不同的取法有多少种?(4)至少有2种不合格商品在内,不同的取法有多少种?(5)至多有2种不合格商品在内,不同的取法有多少种?
解题心得组合问题的两类题型及求解方法(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
对点训练7男运动员6名,女运动员4名,其中男、女队长各1名.现选派5人外出参加比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)队长中至少有1人参加;(4)既要有队长,又要有女运动员.
【例8】 按下列要求分配6本不同的书,各有多少种不同的分配方法?(1)分成三份,1份1本,1份2本,1份3本;(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;(3)平均分成三份,每份2本;(4)平均分配给甲、乙、丙三人,每人2本;(5)分成三份,1份4本,另外两份每份1本;(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本.
解题心得分组、分配问题的一般解题思路是先分组再分配.(1)分组问题属于“组合”问题.①对于整体均分,不管它们的顺序如何,都是一种情况,所以分组后一定要除以组数的阶乘;②对于部分均分,即若有m组元素个数相同,则分组时应除以m!;③对于不等分组,只需先分组,后排列.(2)分配问题属于“排列”问题.①相同元素的“分配”问题,常用的方法是采用“隔板法”;②不同元素的“分配”问题,利用分步乘法计数原理,分两步完成,第一步是分组,第二步是发放;③限制条件的分配问题常采用分类法求解.
对点训练8(1)某科研单位准备把7名大学生分配到编号为1,2,3的三个实验室实习,若要求每个实验室分配到的大学生人数不小于该实验室的编号,则不同的分配方案的种数为(　　)A.280B.455C.355D.350(2)学校将5位同学分别推荐到北京大学、上海交通大学、浙江大学三所大学参加自主招生考试,则每所大学至少推荐一人的不同推荐方法种数为(　　)A.240B.180C.150D.540
答案 (1)B　(2)C
角度1　二项展开式的“赋值问题”例9　(1)若(2x＋ )4＝a0＋a1x＋a2x2＋a3x3＋a4x4，则(a0＋a2＋a4)2－(a1＋a3)2的值为A.－1 B.0 C.1 D.2
所以(a0＋a2＋a4)2－(a1＋a3)2＝(－4＋3)4＝1.
(2)若(3x2－2x＋1)5＝a10x10＋a9x9＋a8x8＋…＋a1x＋a0(x∈C)，求：
①(a0＋a2＋a4＋a6＋a8＋a10)2－(a1＋a3＋a5＋a7＋a9)2；
解　令x＝1，得a0＋a1＋…＋a10＝25；令x＝－1，得(a0＋a2＋a4＋a6＋a8＋a10)－(a1＋a3＋a5＋a7＋a9)＝65.两式相乘，得(a0＋a2＋a4＋a6＋a8＋a10)2－(a1＋a3＋a5＋a7＋a9)2＝25×65＝125.
②－a2＋a4－a6＋a8－a10.
解　令x＝i，得－a10＋a9·i＋a8－a7·i－a6＋a5·i＋a4－a3·i－a2＋a1·i＋a0＝(－2－2i)5＝－25(1＋i)5＝－25[(1＋i)2]2(1＋i)＝128＋128i.整理得(－a10＋a8－a6＋a4－a2＋a0)＋(a9－a7＋a5－a3＋a1)·i＝128＋128i，故－a10＋a8－a6＋a4－a2＋a0＝128.因为a0＝1，所以－a10＋a8－a6＋a4－a2＝127.
反思感悟　“赋值法”在二项展开式中的应用(1)观察：先观察二项展开式左右两边式子的结构特征.(2)赋值：结合待求和上述特征，对变量x赋值，常见的赋值有x＝－1，x＝0，x＝1等，视具体情况而定.(3)解方程：赋值后结合待求建立方程(组)，求解便可.
跟踪训练　若(x2＋1)(x－3)9＝a0＋a1(x－2)＋a2(x－2)2＋a3(x－2)3＋…＋a11(x－2)11，则a1＋a2＋a3＋…＋a11的值为____.
解析　令x＝2，得a0＝(22＋1)(2－3)9＝－5，令x＝3，得a0＋a1＋a2＋a3＋…＋a11＝(32＋1)(3－3)9＝0，所以a1＋a2＋a3＋…＋a11＝－a0＝5.
角度2　二项展开式的特定项问题
(1)求展开式中的所有有理项；
解得n＝10(负值舍去)，
于是有理项为T1＝x5和T7＝13 440.
(2)求展开式中系数的绝对值最大的项；
又因为r∈N，所以r＝7，
解　设第r＋1项系数的绝对值最大，则
又因为当r＝0时，T1＝x5，
解　二项式系数之和为2n＝256，可得n＝8.
解　设常数项为第r＋1项，
故8－2r＝0，即r＝4，
(3)若(x＋m)n展开式中系数最大项只有第6项和第7项，求m的取值情况.
解　易知m>0，设第r＋1项系数最大.
由于只有第6项和第7项系数最大，